OpenGL中矩阵应用场景概念：在3D笛卡尔坐标系, 基本上⼀个顶点就是XYZ坐标空间上的⼀个位置. ⽽在空间中给定的

基础-3D数学
- 向量
  - 概念： 在3D笛卡尔坐标系, 基本上⼀个顶点就是XYZ坐标空间上的⼀个位置. ⽽在空间中给定的⼀个位置恰恰是由⼀个单独的XYZ定义的.⽽这这样的 XYZ 就是向量;
  - 向量长度（模）计算公式：
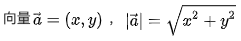
  - 单位向量、单位化向量
    - 单位向量：向量长度为1的向量
    - 单位化向量： 向量的长度不是1，但是通过缩放达到向量长度是1的过程叫做标准化，标准化后的向量称为单位化向量
  - OpenGL中如何定义一个向量-math3d 库
    math3d库，有2个数据类型，能够表示⼀个三维或者四维向量。
    M3DVector3f可以表示⼀个三维向量（x,y,z），
    M3DVector4f则可以表示⼀个四维向量（x,y,z,w).
    在典型情况下，w坐标设为1.0。x,y,z值通过除以w，来进⾏缩放。⽽除以1.0则本质上不改变x,y,z值。
  - 向量点乘
    2个(三维向量)单元向量之间进⾏点乘运算将得到⼀个标量(不是三维向量,是⼀个标量)，它表示两个向量之间的夹⻆;
    点乘的前提条件：2个向量必须为单位向量;
    动作：2个三维向量之间进⾏点乘结果：返回⼀个[-1,1]范围的值. 这个值其实就是夹⻆的cos值(余弦值)
  - 向量叉乘
- 矩阵假设, 在空间有⼀个点.使⽤ xyz 描述它的位置. 此时让其围绕任意位置旋转⼀定⻆度后. 我们需要知道这个点的新的位置. 此时需要通过矩阵进⾏计算; 因为新的位置的x 不单纯与原来的x还和旋转的参数有关. 甚⾄于y和z坐标有关;
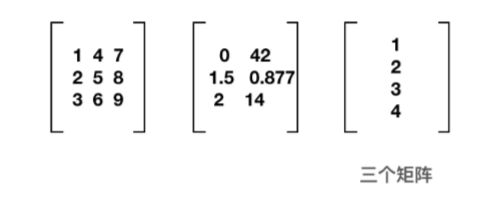
  矩阵只有⼀⾏或者⼀列都是合理的. 只有⼀⾏或者⼀列数字可以称为向量. 也可以称为矩阵; 矩阵相乘注意点：
- 矩阵相乘不满足交换律
- 单位矩阵乘以任何矩阵都不变
- 矩阵相称乘数的列数必须和被乘数的行数相同
- 列向量进⾏了特别的标注：矩阵的最后⼀⾏都为0，只有最后⼀个元素为1
  矩阵在OpenGL的特殊点：
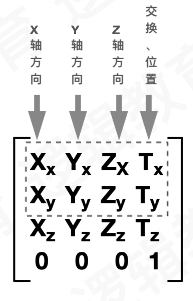
- 在其他编程标准中, 许多矩阵库定义⼀个矩阵时,使⽤⼆维数组; OpenGL的约定⾥,更多倾向使⽤⼀维数组; 这样做的原因是: OpenGL使⽤的是 Column-Major(以列为主)矩阵排序的约定
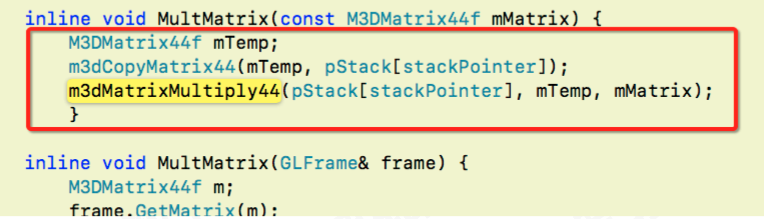
- 矩阵左乘：
  1. 从栈顶获取栈顶矩阵复制到 mTemp
  2. 将栈顶矩阵 mTemp 左乘 mMatrix
  3. 将结果放回栈顶空间⾥

OpenGL中的变化

变换对照表

变换	解释
视图变换	指定观察者位置
模型变换	在场景中移动物体
模型视图	描述视图/模型变换的⼆元性(2种看到模型转换的⽅式)
投影	改变视景体⼤⼩和设置它的投影⽅式
视⼝	伪变化,对窗⼝上最终输出进⾏缩放

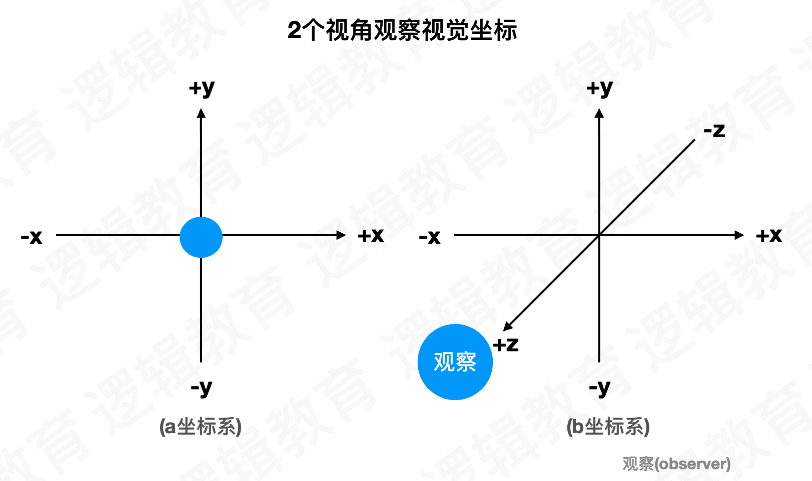
视角观察视觉坐标
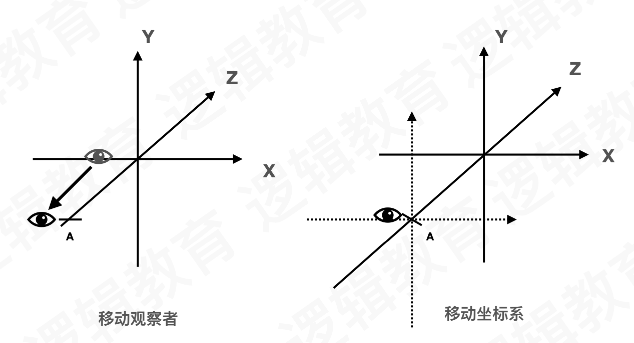
视图变换视图变换是应⽤到场景中的第⼀种变换, 它⽤来确定场景中的有利位置,在默认情况下, 透视投影中位于原点(0,0,0),并沿着 z 轴负⽅向进⾏观察 (向显示器内部”看过去”). 当观察者点位于原点(0,0,0) 时,就像在透视投影中⼀样. 视图变换将观察者放在你希望的任何位置.并允许在任何⽅向上观察场景, 确定视图变换就像在场景中放置观察者并让它指向某⼀个⽅向; 从⼤局上考虑, 在应⽤任何其他模型变换之前, 必须先应⽤视图变换. 这样做是因为, 对于视觉坐标系⽽⾔, 视图变换移动了当前的⼯作的坐标系; 后续的变化都会基于新调整的坐标系进⾏.
模型变换
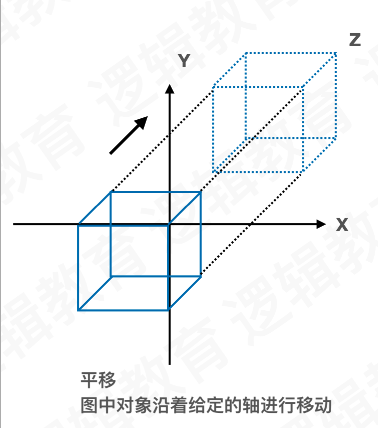
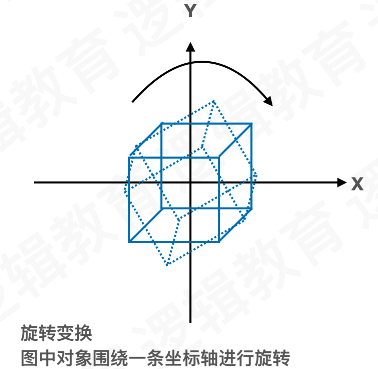
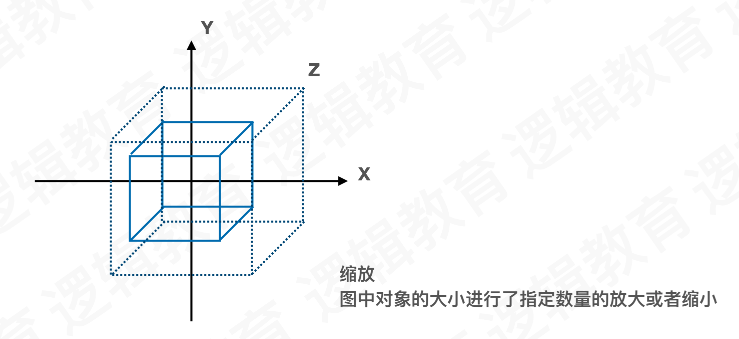
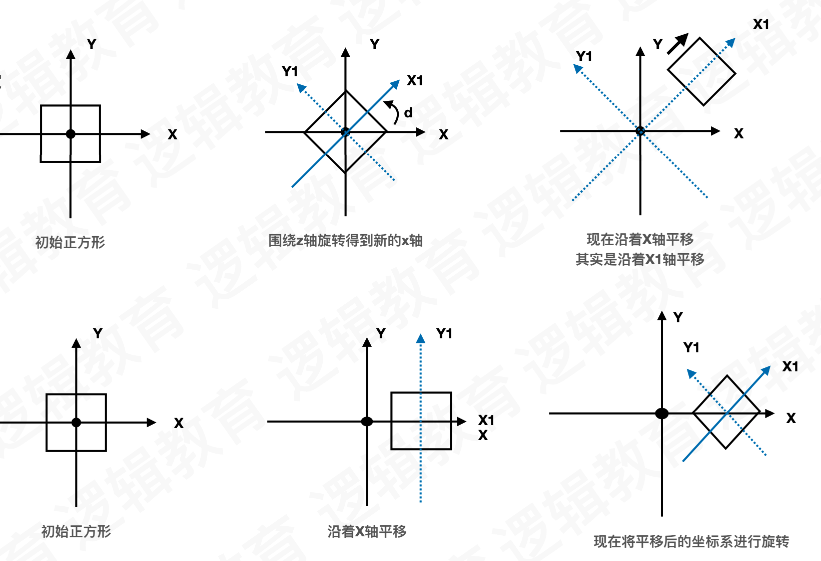
- 概念：⽤于操纵模型与其中某特定变换. 这些变换将对象移动到需要的位置. 通过旋转,缩放,平移
- 两种看待模型变换的方式
- 综合变换 void m3dMatrixMultiply44(M3DMatrix44f product, const M3DMatrix44f a, const M3DMatrix44f b);
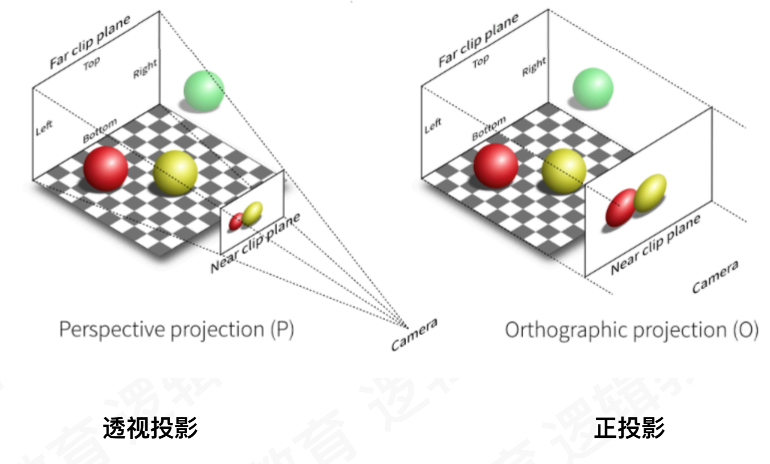
投影变换

矩阵堆栈使用

//类型 
GLMatrixStack::GLMatrixStack(int iStackDepth = 64); //在堆栈顶部载⼊⼀个单元矩阵 
void GLMatrixStack::LoadIdentity(void); 
//在堆栈顶部载⼊任何矩阵 
//参数：4*4矩阵 
void GLMatrixStack::LoadMatrix(const M3DMatrix44f m); //矩阵乘以矩阵堆栈顶部矩阵，相乘结果存储到堆栈的顶部 
void GLMatrixStack::MultMatrix(const M3DMatrix44f); //获取矩阵堆栈顶部的值 GetMatrix 函数 
//为了适应GLShaderMananger的使⽤，或者获取顶部矩阵的副本 
const M3DMatrix44f & GLMatrixStack::GetMatrix(void); void GLMatrixStack::GetMatrix(M3DMatrix44f mMatrix);
//将当前矩阵压⼊堆栈(栈顶矩阵copy ⼀份到栈顶) void GLMatrixStack::PushMatrix(void); 
//将M3DMatrix44f 矩阵对象压⼊当前矩阵堆栈 
void PushMatrix(const M3DMatrix44f mMatrix); //将GLFame 对象压⼊矩阵对象 
void PushMatrix(GLFame &frame); 
//出栈（出栈指的是移除顶部的矩阵对象） 
void GLMatrixStack::PopMatrix(void);

OpenGL中矩阵应用场景

基础-3D数学

向量

OpenGL中的变化

矩阵堆栈使用