关于L2范数在权重衰减中作用的认识简单来说，模型的训练误差远小于它在测试数据集上的误差的现象被称为过拟合，它出现的原因可

最近在学习李沐博士的Gluon-tutorial中关于L2范数正则化能够有效的抑制deep learning过拟合的问题，在  
discuss区看到有人讨论多维范数的相关问题，经过一番推理研究与查阅资料现整理成本文。

过拟合、 $L_2$ 范数与权重衰减的定义

简单来说，模型的训练误差远小于它在测试数据集上的误差的现象被称为过拟合，它出现的原因可能是多种多样的，在这⾥我们重点讨论两个因素：模型复杂度和训练数据集⼤小。
一般而言，给定训练数据集，如果模型的复杂度过低，很容易出现⽋拟合；如果模型复杂度过⾼，很容易出现过拟合；关于训练数据集的大小，如果训练数据集中样本数过少，特别是⽐模型参数数量（按元素计）更少时，则过拟合更容易发⽣。
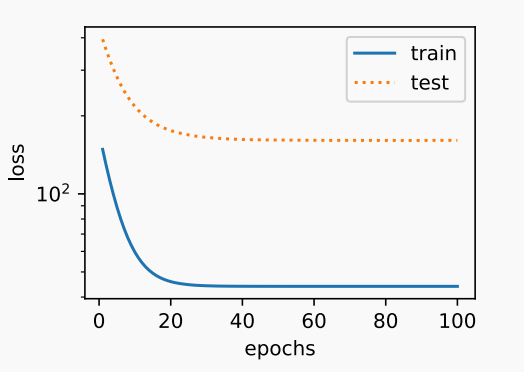
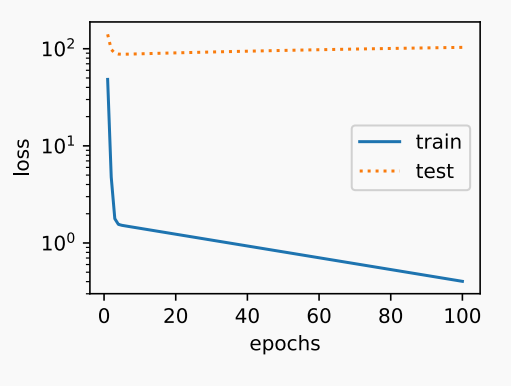
下面我们用一个简单的例子来直观感受下：很显然，使用线性函数去拟合一个三阶多项式函数将出现欠拟合；使用过小的训练样本将造成过拟合。
上图为欠拟合，下图为过拟合

权重衰减是应对过拟合问题的常用解决办法，且权重衰减等价于 $L_2$ 范数的正则化

这是本文想要探讨的问题，既然L2范数可以，那L1范数，L3范数可以吗？

如果对范数不了解推荐看这里

如何通俗易懂地解释「范数」？

下面我们先介绍正常的通过 $L_2$ 范数正则化来抑制过拟合的做法。
首先， $L_2$ 范数正则化是指在模型原损失函数基础上添加 $L_2$ 范数惩罚项，从而得到训练所需要最小化的函数。 $L_2$ 范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积。以线性回归中的损失函数

ℓ(w1,w2,b)= \frac{1}{n}\sum_{i=1}^n\frac{1}{2}(x_1^{(i)}w_1+x_2^{(i)}w_2+b-y^{(i)})^2

为例，其中 $w_1$ , $w_2$ 是权重参数， $b$ 是偏差参数，样本 $i$ 的输入为 $x_1^{(i)}$ , $x_2^{(i)}$ ,标签为 $y^{(i)}$ ，样本数为 $n$ 。将权重参数用向量 $w$ =[w1,w2]表示，带有 $L_2$ 范数惩罚项的新损失函数为

其中超参数 $λ>0$ 。当权重参数均为0时，惩罚项最小。当 $λ$ 较大时，惩罚项在损失函数中的比重较大，这通常会使学到的权重参数的元素较接近0。当 $λ$ 设为0时，惩罚项完全不起作用。上式中 $L_2$ 范数平方 $||w||^2$ 开后得到 $w_1^2+w_2^2$ 。有了 $L_2$ 范数惩罚项后，在小批量随机梯度下降中，我们将线性回归中权重 $w_1$ 和 $w_2$ 的迭代方式更改为

(1-ηλ)w_1-\frac{η}{|B|}\sum_{i\in B}x_1^{(i)}(x_1^{(i)}w_1+x_2^{(i)}w_2+b-y^{(i)})\to w_1 ,

(1-ηλ)w_2-\frac{η}{|B|}\sum_{i\in B}x_2^{(i)}(x_1^{(i)}w_1+x_2^{(i)}w_2+b-y^{(i)})\to w_2 .

可见， $L_2$ 范数正则化令权重 $w_1$ 和 $w_2$ 先自乘小于1的数，再减去不含惩罚项的梯度。因此， $L_2$ 范数正则化又叫权重衰减。权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制，这可能对过拟合有效。实际场景中，我们有时也在惩罚项中添加偏差元素的平方和。

权重衰减的实际效果

了解完原理下面我们使用Gluon自带的权重衰减参数weight_decay进行测试,原型是一个高斯线性回归函数。

其中噪声项 ϵ 服从均值为0、标准差为0.01的正态分布。为了较容易地观察过拟合，我们考虑高维线性回归问题，如设维度 $p=200$ ；同时，我们特意把训练数据集的样本数设低，如25。

函数定义如下

%matplotlib inline
import d2lzh as d2l
from mxnet import autograd, gluon, init, nd
from mxnet.gluon import data as gdata, loss as gloss, nn

n_train, n_test, num_inputs = 25, 100, 200
true_w, true_b = nd.ones((num_inputs, 1)) * 0.01, 0.05

features = nd.random.normal(shape=(n_train + n_test, num_inputs))
labels = nd.dot(features, true_w) + true_b
labels += nd.random.normal(scale=0.01, shape=labels.shape)
train_features, test_features = features[:n_train, :], features[n_train:, :]
train_labels, test_labels = labels[:n_train], labels[n_train:]

我们直接在构造Trainer实例时通过wd参数来指定权重衰减超参数。默认下，Gluon会对权重和偏差同时衰减。我们可以分别对权重和偏差构造Trainer实例，从而只对权重 $w$ 衰减。

def fit_and_plot_gluon(wd):
    net = nn.Sequential()
    net.add(nn.Dense(1))
    net.initialize(init.Normal(sigma=1))
    # 对权重参数衰减。权重名称一般是以weight结尾
    trainer_w = gluon.Trainer(net.collect_params('.*weight'), 'sgd',
                              {'learning_rate': lr, 'wd': wd})
    # 不对偏差参数衰减。偏差名称一般是以bias结尾
    trainer_b = gluon.Trainer(net.collect_params('.*bias'), 'sgd',
                              {'learning_rate': lr})
    train_ls, test_ls = [], []
    for _ in range(num_epochs):
        for X, y in train_iter:
            with autograd.record():
                l = loss(net(X), y)
            l.backward()
            # 对两个Trainer实例分别调用step函数，从而分别更新权重和偏差
            trainer_w.step(batch_size)
            trainer_b.step(batch_size)
        train_ls.append(loss(net(train_features),
                             train_labels).mean().asscalar())
        test_ls.append(loss(net(test_features),
                            test_labels).mean().asscalar())
    d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
                 range(1, num_epochs + 1), test_ls, ['train', 'test'])
    print('L2 norm of w:', net[0].weight.data().norm().asscalar())

观察过拟合

fit_and_plot_gluon(0)
注意此时权重衰减为 $0$

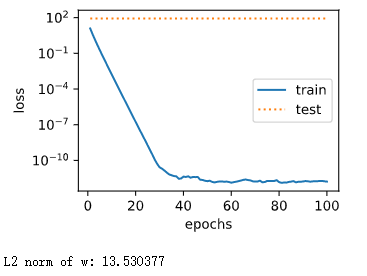
使用权重衰减

fit_and_plot_gluon(10)

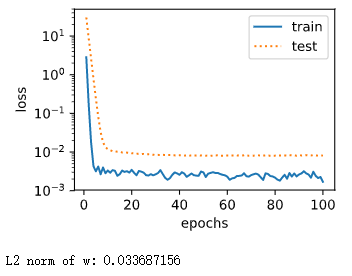
结论

到此为止我们发现，确实通过设置参数wd可以减小w和w的 $L_2$ 范数做到对权重的衰减作用,在这个例子中就具体为

后续测试L1范数与L3范数

L1范数

首先是 $L_1$ _norm最重要的一个特点，输出稀疏，会把不重要的特征直接置零，而 $L_2$ _norm则不会。^[1]

这点可以从L1、L2正则项的偏导中直接推算出来，

于是会发现，在梯度更新时，不管 $L_1$ 的大小是多少（只要不是0）梯度都是1或者-1，所以每次更新时，它都是稳步向0前进。 $L_2$ 则不同，梯度越靠近0，就会变得越来越小，但始终不能达到0。
综上， $L_1$ 正则的话基本上经过一定步数后很可能变为0，而 $L_2$ 几乎不可能，因为在值小的时候其梯度也会变小。于是也就造成了 $L_1$ 输出稀疏的特性，不能用于权重衰减。

L3范数

其实关于更高维度的范数我们还可以有 $L_∞$ ,

关于这个问题我暂时只想到了数学层面应该是可以通过多次求导实现权重衰减的，但是由于计算量比 $L_2$ 大所以并不值得这么去做，而且超越了三维空间貌似物理解释也很难。更多的讨论请看这里：

Why do we only see L1 and L2 regularization but not other norms?

理解L1，L2 范数在机器学习中应用. ↩︎

关于L2范数在权重衰减中作用的认识

过拟合、范数与权重衰减的定义