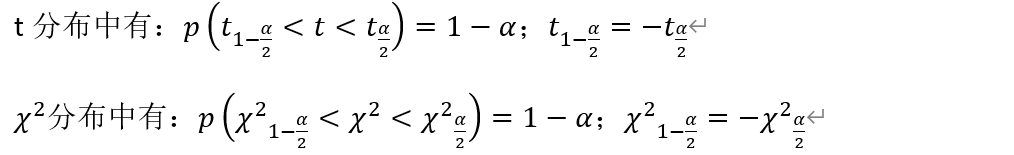一、数据的分类

- 注:低级数据的方法高级数据可用,高级数据的方法低级数据不可用。
二、常见术语
- 总体和样本
- 参数和统计量
- 参数:研究的总体的某种特征值,如均值μ、标准差σ、比例π。
- 统计量:根据样本计算的样本的某个特征值,如均值x_bar、标准差s、比例p。
- 变量
- 描述事物某种特征的概念,如销售额、产品质量。
三、常见分布
1. 两点分布与二项分布
- 形式: 两点分布:X~B(1,p)
| X | 0 | 1 |
|---|---|---|
| 概率 | 1-p | p |
- E(X)=p;D(X)=p(1-p)
- 二项分布:X~B(n,p)
- E(X)=np;D(X)=np(1-p)
2. 正态分布:X~N(μ,σ^2)
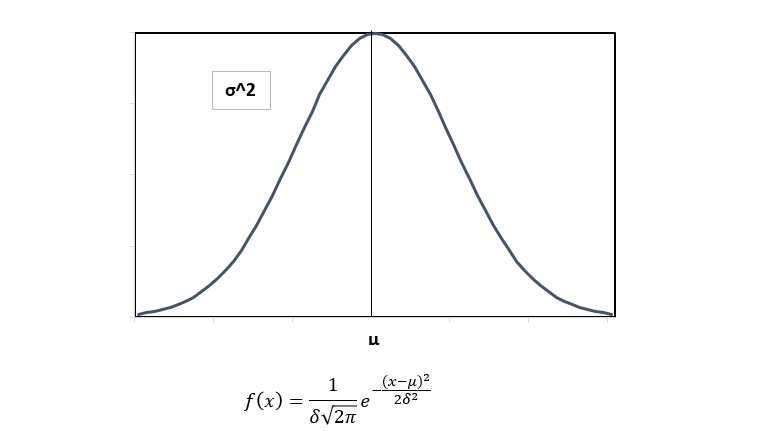
- E(X)=μ;D(X)=σ^2
- 注:曲线下的总面积=1。
- 标准正态分布X~N(0,1)
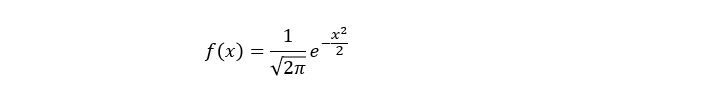
- E(X)=0;D(X)=1
- 注:计算一般正态分布的概率时,先将其转化为标准正态分布再计算。
3. 卡方X^2分布
- 定义:当X1,X2,...XN相互独立且服从标准正态分布时,其平方和(X1^2+...+Xn^2)服从卡方分布(n)。
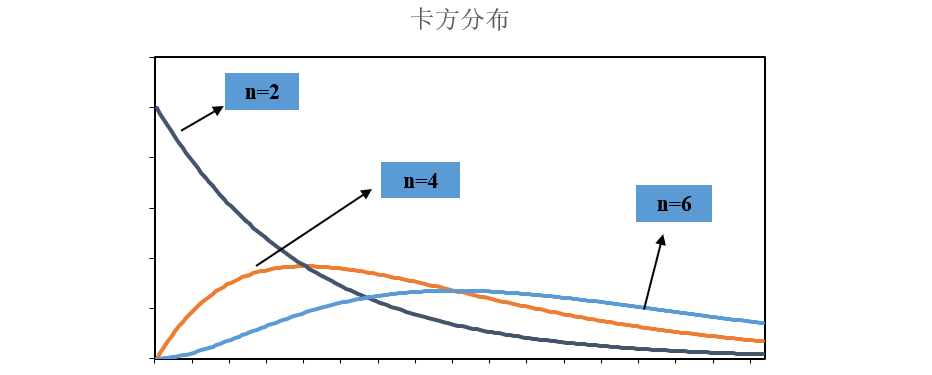
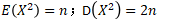
- 注:可加性U+V~X^2(n1+n2);当n—>+∞时极限是正态分布。
4. t分布
- 定义:当X~N(0,1)、Y~X^2(n)且X、Y相互独立时,t=X/sqrt(Y/n)服从t分布(n)。
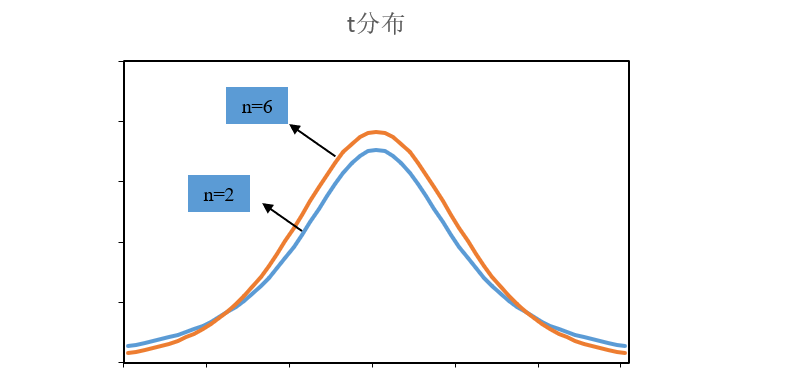
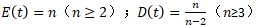
- 注:n≥30时,t分布越来越接近标准正态分布;用于小样本。
5. F分布
- 定义:U~X^2(m)、V~X^2(n)且U、V相互独立,则F=(U/m)/(V/n)服从F分布(m,n)。
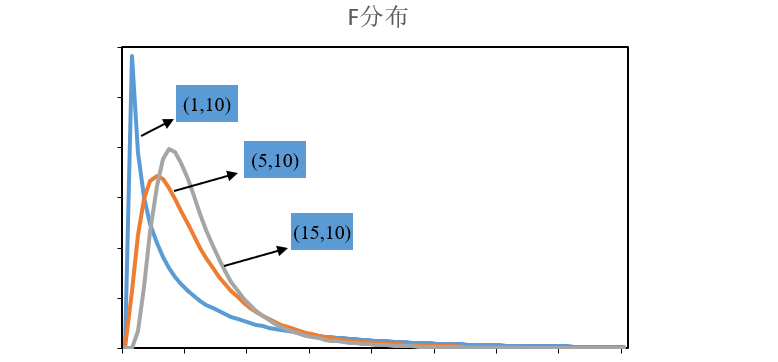
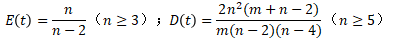

- 注:F分布用于方差分析、回归方程的显著性检验等。
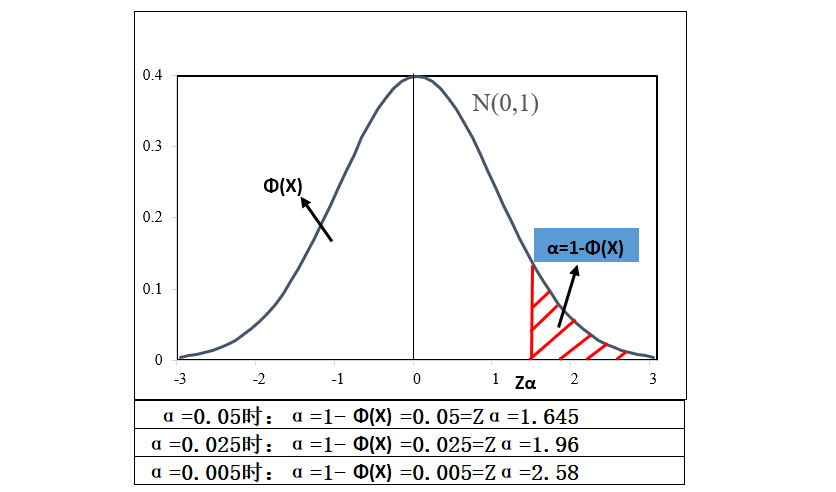
四、分布函数与分位点
- 分布函数Φ(X): 在N(0,1)中X=x左侧的面积,P(X≤x)=1-α
- 分位点Zα: 在N(0,1)中,右侧面积为α的点,P(X≥Zα)=α