本文参考labuladong的文章,重在自我梳理,图片也来源于此。
算法介绍
动态规划在算法思想中十分重要,可以用来解决许多求最值问题。
本文会讲解动态规划的基本思路,以及递归问题如何转化为动态规划问题。但需要注意,递归问题有的时候也会用来求组合,这个时候动态规划可能并不是最佳选择。
算法描述
动态规划问题的一般形式就是求最值。
既然求最值,核心问题是什么呢?就是讲可能的情况穷举出来。 穷举看似简单,但是算法中往往存在重复计算的问题。动态规划的穷举,就是讲这些已计算的值存下来,去除无效计算。简而言之,就是这类问题存在重叠子问题
动态规划问题一定会具备最优子结构,这样才能拆解成子问题进行求值。
动态规划问题一般会有一个数据计算公式,可以描述与子问题的关系,即状态转移方程。而写出状态转移方程往往是最困难的,我们可以做题前找找规律。
算法实践-斐波拉契数列
这个是最经典的递归问题,但是递归往往会带来重复计算的问题,同时递归一般也可以转化为动态规划。
原因是因为,两者都需要状态转移方程和拆解子问题。
暴力递归
function f(n){
if (n == 1 || n == 2) return 1;
return f(n-1) + f(n-2);
}
递归问题建议列举出递归树,这样可以寻找规律,进行优化。
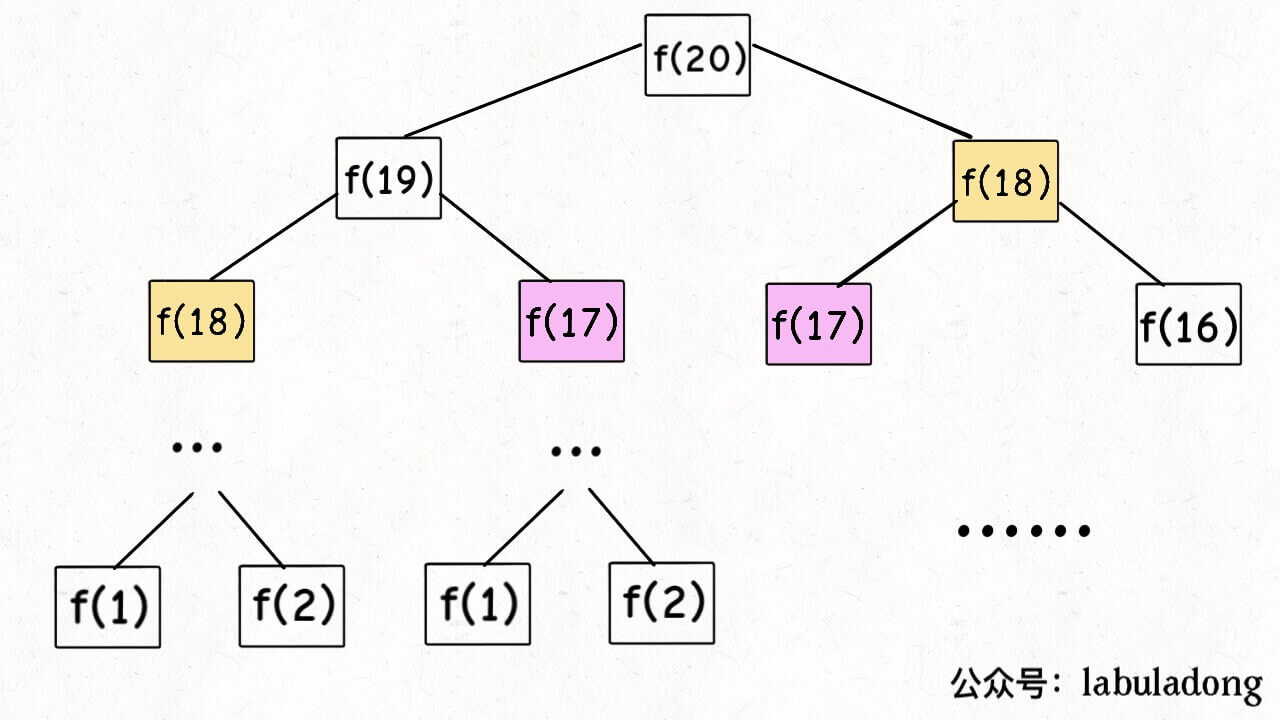
缓存递归
我们可以设置一个备忘录,记录我们已经计算过的子问题,如果这个子问题已存在于备忘录,那么直接返回。 一般是使用数组来做备忘录,如果问题相关因子较多,就是多维数组。
function fib(n){
var arr = new Array(n+1, 0); // 先建立一个数组
function f(n, arr){
if (n == 1 || n == 2) return 1;
if (arr[n] !=0 ) return arr[n];
arr[n] = f(n-1, arr) + f(n-2, arr);
return arr[n];
}
return f(n, arr);
}
通过备忘录arr,我们可以去除无效计算,如下图:
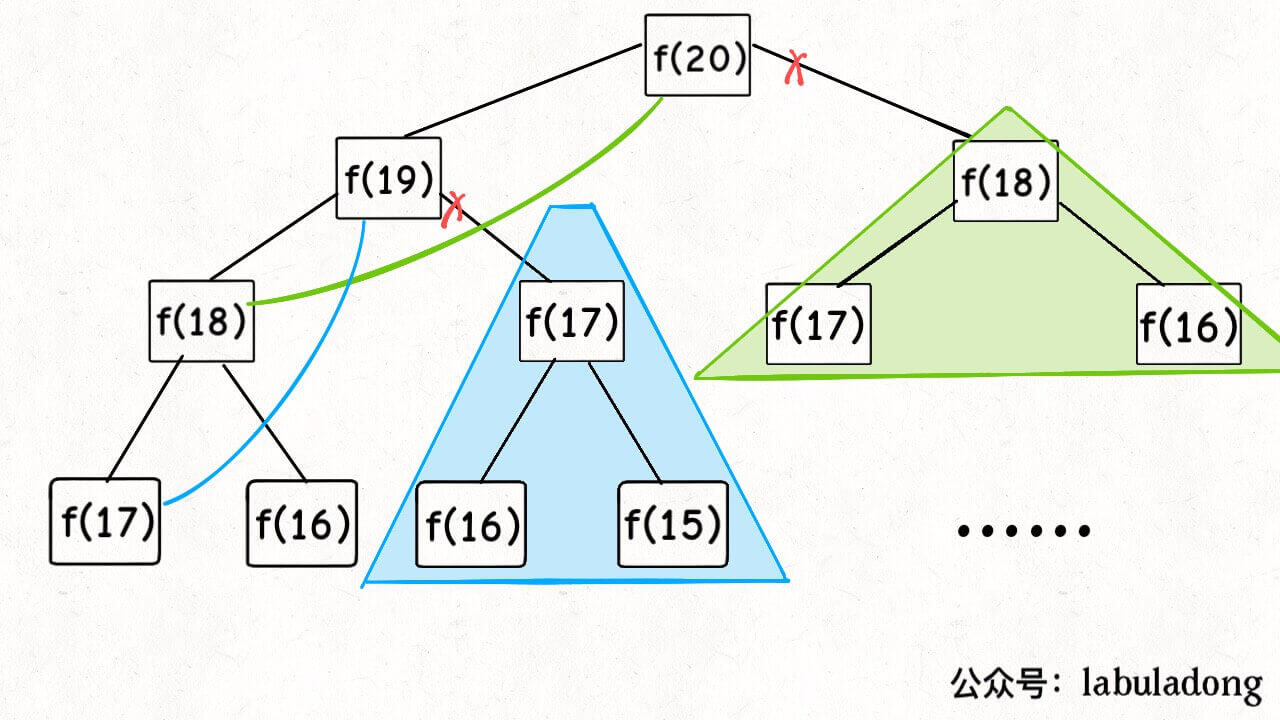
因为真正需要计算的是f(1)到f(n),所以计算了n次。时间复杂度是O(n);
再梳理一下,递归往往是,先计算f(n), 然后计算f(n-1),f(n-2)。
只不过通过栈的方式,将最后计算的值依次向上返回,得到f(n)。
当前算法中没有列出栈,但是Js函数执行就是一个调用栈(LIFO)的执行顺序。这种方式是自上而下的。
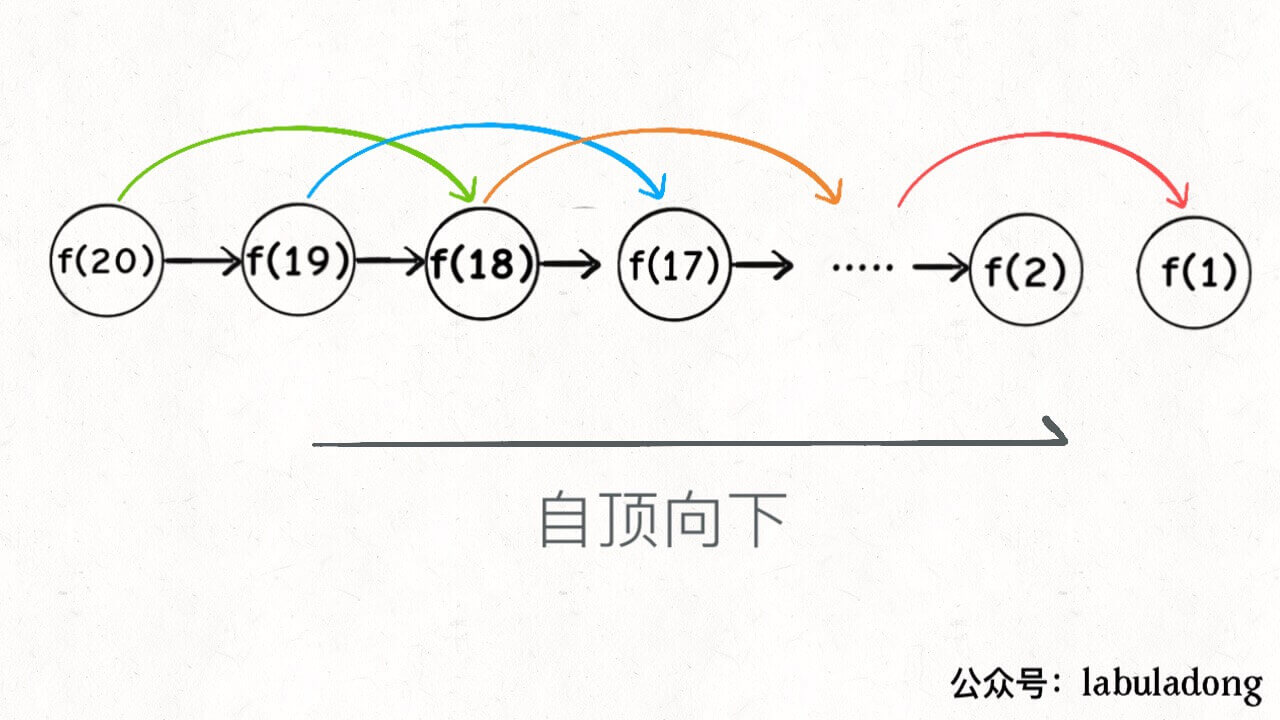
如果换个思路,自下而上,就是首先从问题规模最小的f(1)和f(2)开始往上推,直到推到我们想要的答案f(20)。
这个,就是动态规划的思路。所以动态规划往往采用队列(FIFO)的方式去做,一般会用循环实现。
动态规划
我们这次按照算法思路方式去看这个问题:
最优子结构,就是f(n)可以通过f(n-1)和f(n-2)得到, 最小问题的f(1)和f(2);
状态转移方程:
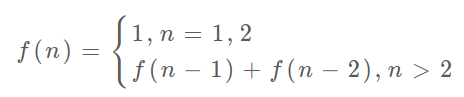
通过以上解析,我们先得到最简单规模的值,f(1) =1 , f(2) = 1;
然后推理出f(3) = f(2) + f(1), f(4) = f(3) + f(2), ...
function fib(n){
if (n == 1 || n == 2) return 1;
var arr = new Array(n+1);
arr[1] = 1;
arr[2] = 1;
for (var i = 3; i <= n; i++ ){
arr[i] = arr[i-1] + arr[i-2];
}
return arr[n];
}