Leecode 03 无重复字符的最长子串

题目

给定一个字符串，请你找出其中不含有重复字符的最长子串的长度。

示例 1:

输入: "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: "bbbbb" 输出: 1 解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。请注意，你的答案必须是子串的长度，"pwke" 是一个子序列，不是子串。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/longest-substring-without-repeating-characters

暴力解法

从前向后进行遍历，这个是自己第一反应能想到的，但是时间复杂度明显很高O(n3)。优化解法是参考了别人的解法才想到的。

public int lengthOfLongestSubstring1(String s) {
        int result = 0;
        for (int i = 0; i < s.length(); i++) {
            // 遍历子串的终止字符
            for (int j = i + 1; j < s.length(); j++) {
                if (allUnique(s, i,j)) {
                    result = Math.max(j - i, result);
                }
            }
        }
        return result;
    }

    private boolean allUnique(String s, int start, int end) {
        Set<Character> set = new HashSet<>();
        for (int i = start; i < end; i++) {
            char c = s.charAt(i);
            if (set.contains(c)) {
                return false;
            } else {
                set.add(c);
            }
        }
        return true;
    }

滑动窗口

根据题目中的关键字：重复字符 -> 出现1次

涉及到子串，考虑滑动窗口

通过使用HashSet作为一个滑动窗口，检查一个字符是否已经存在于现有的子字符中只需要O(1). 滑动窗口经常作为一个抽象的概念来处理数组/字符串问题。窗口代表着一组数据/字符串元素，通过开头和结尾的索引来定义窗口。

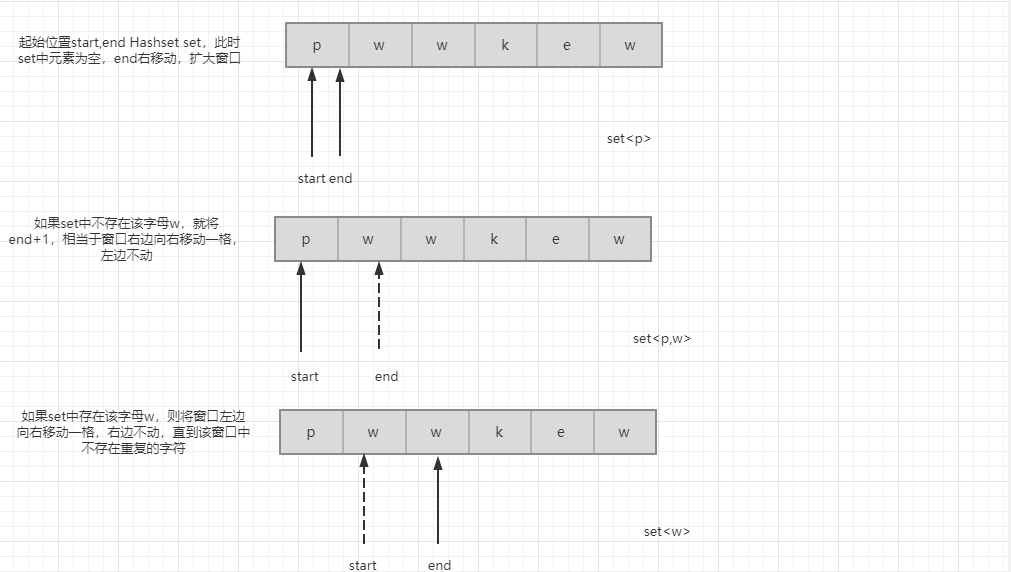
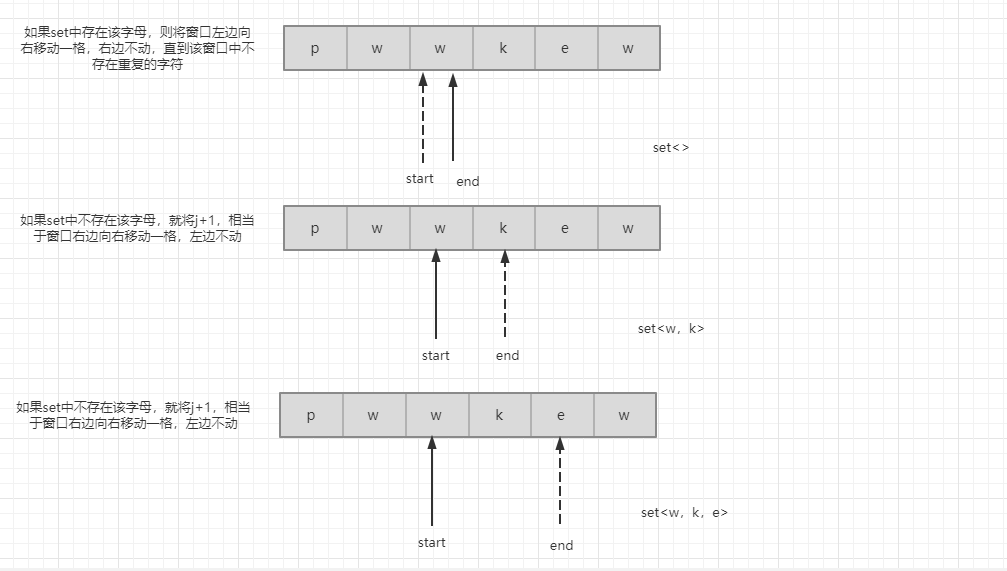
public int lengthOfLongestSubstring2(String s) {
        int result = 0;
        if (null == s) {
            return result;
        }
        int start = 0, end = 0;
        int len = s.length();
        HashSet<Character> set = new HashSet<>();
        while (end < len){
            if (!set.contains(s.charAt(end))) {
                set.add(s.charAt(end++));
                result = Math.max(result, end - start);
            }else {
                set.remove(s.charAt(start++));
            }
        }

        return result;
    }

该方法是使用Hashset保存窗口中的元素，最坏的情况下需要O(2n)

优化的滑动窗口算法

上面的滑动窗口算法最多需要2n的步骤，但这其实是能被优化为只需要n步。我们可以使用HashMap定义字符到索引之间的映射，然后，当我们发现子字符串中的重复字符时，可以直接跳过遍历过的字符了。

public int lengthOfLongestSubstring3(String s) {
        int result = 0;
        if (null == s) {
            return result;
        }
        HashMap<Character, Integer> map = new HashMap<>();
        for (int start=0, end = 0; end < s.length(); end++) {
            if (map.containsKey(s.charAt(end))) {
                // 当发现重复的字符时,将字符的索引与窗口的左边进行对比，将窗口的左边直接跳到该重复字符的索引处
                start = Math.max(map.get(s.charAt(end)), start);
            } else {
                //记录子字符串的最大的长度
                result = Math.max(result, end - start + 1);
                //map记录第一次遍历到key时的索引位置，j+1,保证i跳到不包含重复字母的位置
                map.put(s.charAt(end), end + 1);
            }
        }
        return result;
    }

本文使用 mdnice 排版