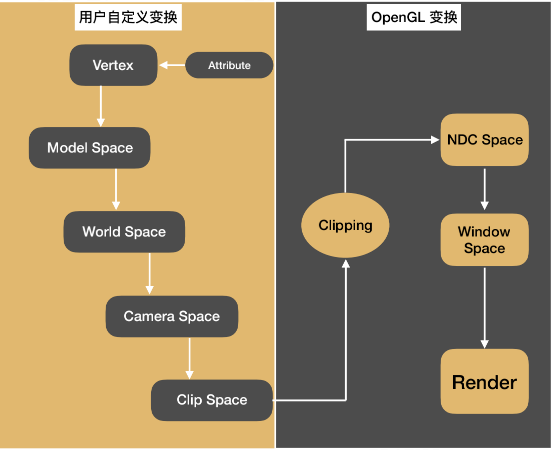
坐标系统

在OpenGL中比较重要的总共有5个坐标系统：

• 局部空间(Local Space，或者称为物体空间(Object Space))
• 世界空间(World Space)
• 观察空间(View Space，或者称为视觉空间(Eye Space))
• 裁剪空间(Clip Space)
• 屏幕空间(Screen Space)

多坐标系统的由来

OpenGL在每次顶点着色器运行之后，希望可见的顶点都可以转化为标准化设备坐标(Normalized Device Coordinate, NDC)，也就是说，每个顶点的x，y，x坐标都应该在（-1.0，1，0）之间，超出这个坐标范围的顶点都将不可见。通常我们会自定一个坐标的范围，之后再在顶点着色器中将这些坐标转换为标准化设备坐标。然后将这些标准化的坐标传入光栅器，变换为屏幕上的二维坐标或者像素。

将原始坐标转化为标准化设备坐标，再转化为屏幕坐标通常是分步骤进行的，类似于流水线的样子。在流水线中，物体的顶点最终转为屏幕坐标之前还会经过多个坐标系统的转换。这样做的好处在于，在特定的坐标系统中，我们只需要关心特定的操作，相当于将复杂的转换过程拆分成了不同的小步骤，更有利于操作和运算。

转换的流程

在坐标转换的过程中，我们需要用到几个变换矩阵，分别是：

• 模型矩阵（Model Matrix）
• 观察矩阵（View Matrix）
• 投影矩阵（Projection Matrix）

下图展示了将一个立方体展示到屏幕上所经过的不同的坐标系的转换流程。

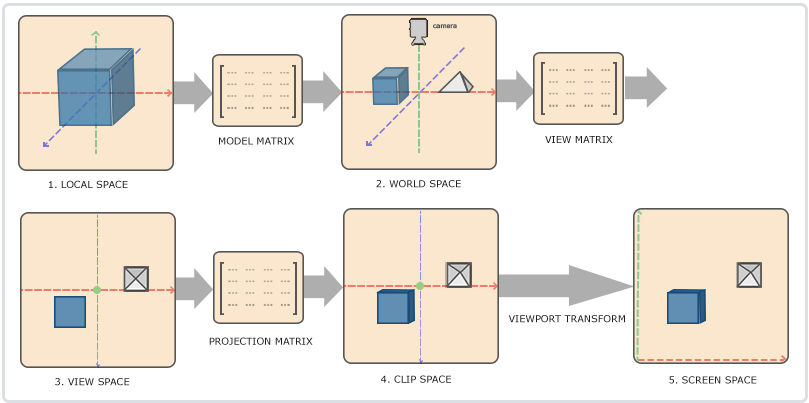
1. 局部坐标是对象相对于局部远点的坐标，也就是物体的起始坐标
2. 局部坐标经过模型矩阵的变换之后变为世界坐标，在当前世界空间的全部物体都是相对于世界坐标原点进行摆放。例如上图中将立方体转换之后可以看到世界空间中还存在一个三角锥体。
3. 接下来将世界坐标转换为观察空间坐标，使得每个坐标都是从摄像机或者观察者的角度进行观察。
4. 通过投影矩阵将观察空间投影到裁剪空间，裁剪坐标会被处理到-1.0到1.0之间，并判断哪些顶点会出现在屏幕上。
5. 将裁剪坐标转换为屏幕坐标，这一过程需要用到视口变换，视口变换将位于-1.0到1.0范围的坐标转换到由glViewPort函数定义的坐标范围内。最后变换出来的坐标将会送到光栅器，转化为像素。

之所以将顶点转换到不同的空间是因为有些操作在特定的坐标系中才有意义。

• 当需要对物体进行修改时，在局部空间中操作会相对合理，因为不涉及和其他物体的关系
• 当需要对物体做出相对于其他物体位置的操作时，在世界坐标系中才说的通。

局部空间

局部空间是物体所在的坐标空间，即对象开始的开始的地方。模型的所有顶点都在局部空间中，他们相对于物体来说都是局部的。

不管物体处于何种的状态，它和物体坐标系的关系是固定的，不会发生改变

世界空间

在世界空间中，每一个物体都有自己的位置，当然，不同的物体也有可能重叠在同一个位置上。世界空间坐标是指物体的顶点相对于世界的坐标，此时世界空间内可能会存在很多个物体，从局部空间到世界空间的变换是通过模型矩阵来实现的。

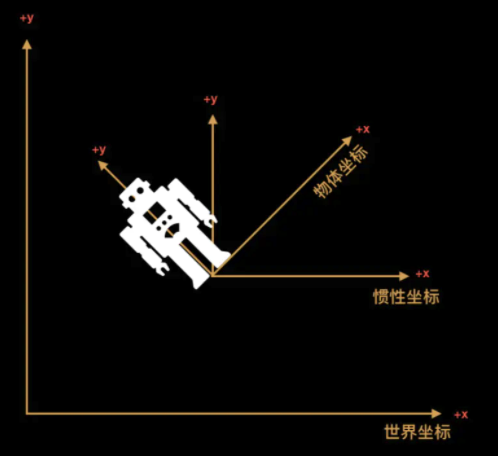
物体坐标转换到世界坐标中，还有一个惯性坐标的概念。

惯性坐标的原点和物体坐标重合，但是惯性坐标的x，y，z轴和世界坐标的x，y，z轴是平行的，这样做的好处是从物体坐标转换到惯性坐标只需要旋转，从惯性坐标到世界坐标只需要平移。

观察空间

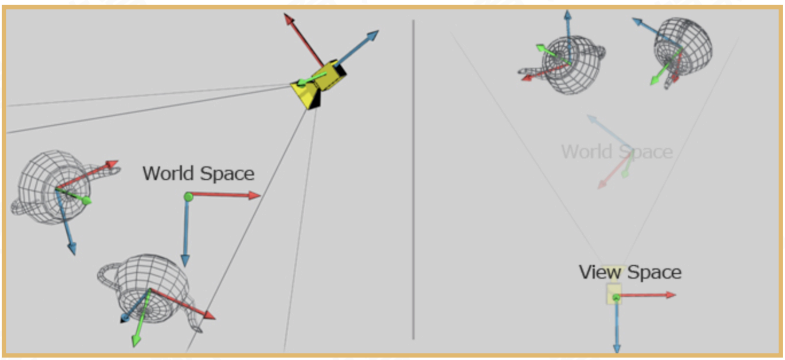
观察空间有时候也被成为摄像机空间或视觉空间。观察空间是将世界空间坐标转化为用户视野前方的坐标而产生的结果。上图显示的是世界空间转换到观察空间的过程。

1. 在世界空间中，假定有一个摄像机从某个角度来观察两个水壶
2. 以摄像机为坐标原点，以摄像机的正面为z-轴的左手坐标系为观察空间的坐标系。

裁剪空间

顶点着色器运行的最后，OpenGL希望所有的坐标都落在一个特定的范围内，且在这个范围外的点都应该被裁掉，剩下的坐标会变成屏幕上可见的片段。

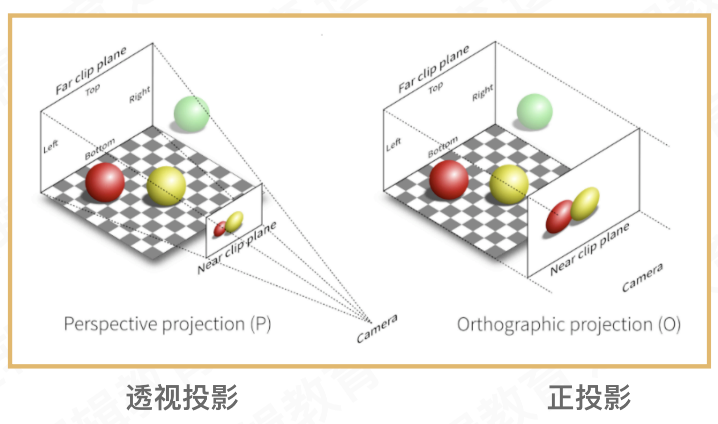
观察坐标变为裁剪坐标的投影矩阵分为两种：

OpenGL坐标变换全局图

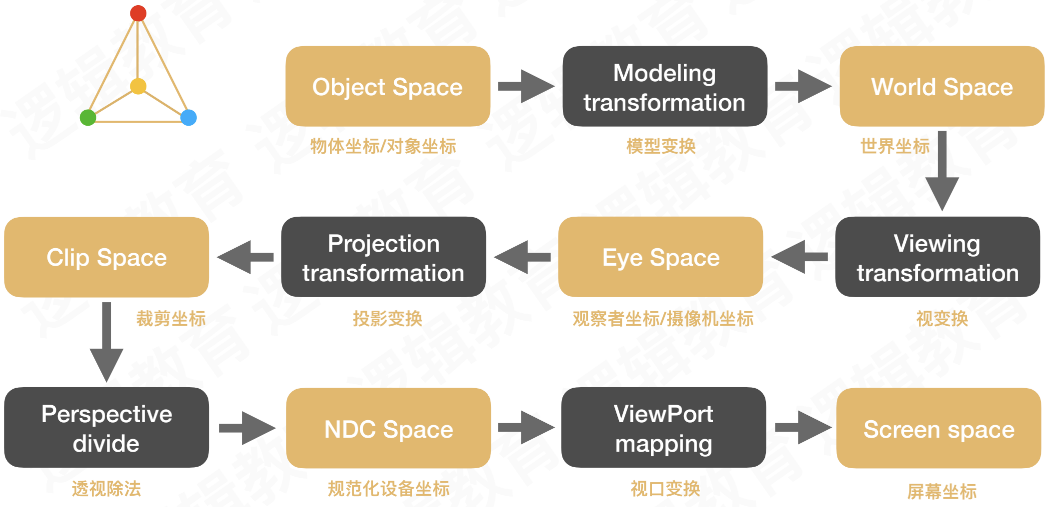
在上图中，OpenGL定义了后三个坐标系（裁剪坐标、NDC坐标、屏幕坐标），前三个坐标（物体坐标、世界坐标、摄像机坐标）是为了用户方便而自定义的坐标。