-
冒泡排序
-
初级版本
思路很简单,就是两层循环将小的数组网上排就好 相关代码:
//排序常用交换函数实现 //交换L中数组r的下标为i和j的值 void swap(int *list,int i,int j) { int temp=list[i]; list[i] = list[j]; list[j] = temp; } //数组打印 void print(int *list,int size) { int i; for(i=0;i<size;i++) printf("%d,",list[i]); printf("\n"); } //冒泡排序(初级版本其实就是交换排序) Status BubbleSort(int *list,int size){ for(int i = 0; i < size; i ++){ for(int j = i + 1; j < size; j ++){ if(list[i] > list[j]){ swap(list, i, j); } } } return OK; } -
正宗冒泡排序
思路:尽可能的每一次排序都将最大的数字往下沉,内层循环相邻的两个树比较交换和初阶版本的区别在于会将大的数字后后排举个例子8,5,6,10 初阶版本的结果就是8,5,6,10,但是下面算法的结果是5,6,8,10,(当然也有特殊情况比如数组是逆序的 10,9,8,7,那么完整版的效率就和初阶版本的效率是一样的) 代码实现:
//冒泡排序(完整版本) //实现思路:尽可能的每一次排序都将最大的数字往下沉, //内层循环相邻的两个树比较交换 //和初阶版本的区别在于会将大的数字后后排举个例子 //8,5,6,10 初阶版本的结果就是8,5,6,10,但是下面算法的结果是 //5,6,8,10,(当然也有特殊情况比如数组是逆序的 10,9,8,7,那么完整版的效率就和初阶版本的效率是一样的) Status BubbleSort1(int *list,int size){ for(int i = 0; i < size; i ++){ for(int j = 0; j < size - i - 1; j ++){ if(list[j] > list[j + 1]){ swap(list, j, j+1); } } print(list, 10); } return OK; } -
正宗冒泡排序优化
思路:还是上述排序,但是需要设置一个标记flag,用来标记后续的数据是不是有序的,如果是有序的则可以直接跳出循环了,排序成功举个列子8,7,9,10 按照上述排序第一次循环的结果是7,8,9,10,第二次循环发现并没有交换,就说明后面的数据是有序的所以就可以直接跳出循环了
实现代码:Status BubbleSort2(int *list,int size){ Status flag = TRUE; for(int i = 0; i < size && flag; i ++){ flag = FALSE; for(int j = 0; j < size - i - 1; j ++){ if(list[j] > list[j + 1]){ swap(list, j, j+1); //如果存在数据交换则说明不是有序的 flag = TRUE; } } } return OK; }
-
-
简单选择排序
思路:两层循环第一次循环找到最小数然后插入到第一个位置第二次循环冲第二个位置开始 找到最小的数字插入到第二个位置依次类推
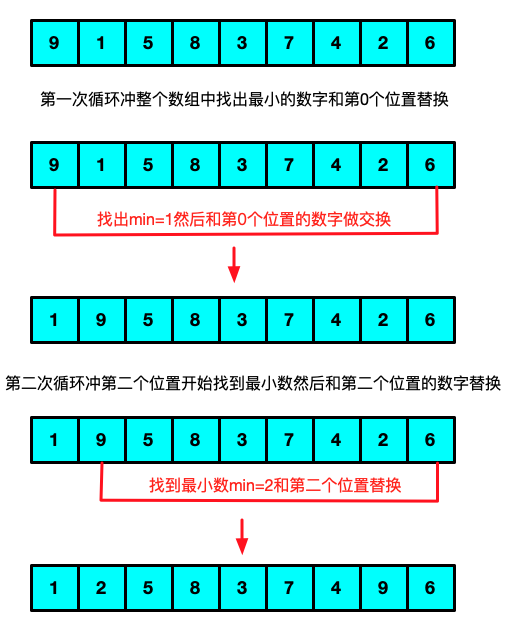
实现代码:``` //简单选择排序 //思路:第一次循环就当第一个数是整个数组的最小值, //开始便利数组如果存在更小的值则替换最小值的索引 //最后再判断,如果最小值的索引和当前循环的第一个值 //索引相同则说明当前循环的第一个值就是最小值,否则 //需要替换最小值和当前循环的第一个值的内容,以此循环下去 Status SelectSort(int *list, int size){ int min = 0; for(int i = 0; i < size; i ++){ min = i; for(int j = i + 1; j < size; j ++){ if(list[min] > list[j]){ min = j; } } if(min != i) swap(list, i, min); } return OK; } ``` -
直接插入排序
思路:冲第二个数开始和前一个数比较如果小于前一个则当前这个数和前一个数互换一下位置如果大于前一个数(则说明当前这个数大于前面的所有的数字应为是有序的),则冲第三个数开始继续上述操作
实现代码://直接插入排序 //思路:冲第二个数开始和前一个数比较如果小于前一个则当前这个数和前一个数互换一下位置 //如果大于前一个数(则说明当前这个数大于前面的所有的数字应为是有序的),则冲第三个数 //开始继续上述操作 Status InsertSort(int *list, int size){ if(size == 1) return OK; for(int i = 1; i < size; i ++){ //当前索引 int n = i; for(int j = i-1; j > 0; j --){ if(list[n] > list[j]){ break; }else{ swap(list, n, j); n = j; } } } return OK; } -
希尔排序
思路:将数组分成小段进行排序,然后不断的缩减分割的长度最后当分割长度是1的时候获得排序结果就是最终结果
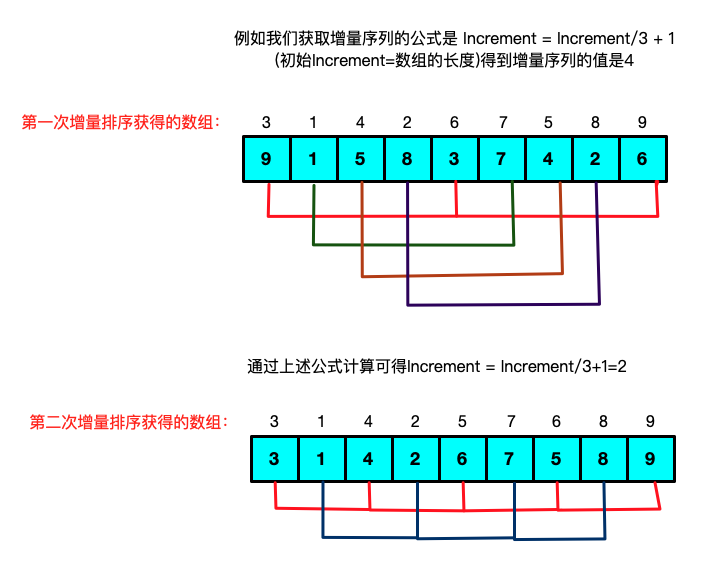
代码实现:``` //希尔排序 //思路:中心思想就是将数组查分成一小段一小段进行排序,没排序完成一次就缩短小段 //数组的长度,知道所称1位置 缩成1之后的排序就是最终结果 Status shellSort(int *list, int size){ int temp; // 用于存放临时变量 int increment = size; do { //计算增量公式,保证每次拍寻晚一次之后呢就缩短分割小段的长度 increment = increment/5; for(int i = increment; i < size; i ++){ if(list[i - increment] > list[i]){ //前面一个数字大于后面一个数字,需要将数组进行调整,做到局部有序 //(就是要满足分割的小段是有序的) temp = list[i]; //往前寻找小于temp的索引(索引跨度是increment)找到之后直接 //将temp插入(应为前面的序列都在前几次的循环对比过是有序的序列) //所以不需要诸葛比较只要找到小于temp的索引直接插入就好剩下的一次往后移动 int j; for(j = i - increment; j > 0 && list[j] > temp; j -= increment){ list[j+increment] = list[j]; } list[j+increment] = temp; } } } while (increment > 1); return OK; } ``` -
堆排序
思路:将数组构建一个二叉树;二叉树要满足所有的结点均大于自己的左右两个孩子结点(大顶堆,小顶堆则反之),构建成功之后将根节点和最后一个叶子结点互换,然后再将冲根节点到倒数第二个结点在组建一个大顶堆然后将根节点和倒数第二个结点进行互换以此类推(有点像选择排序的实现过程)
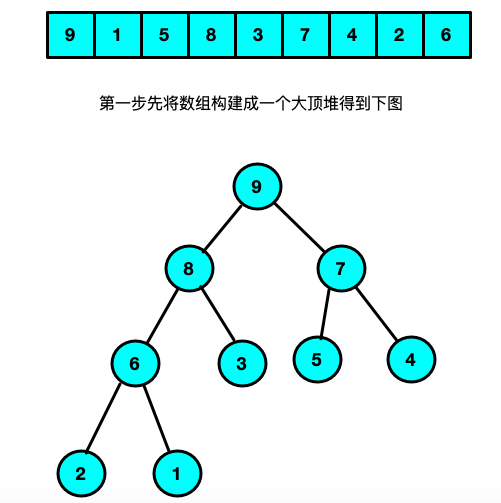
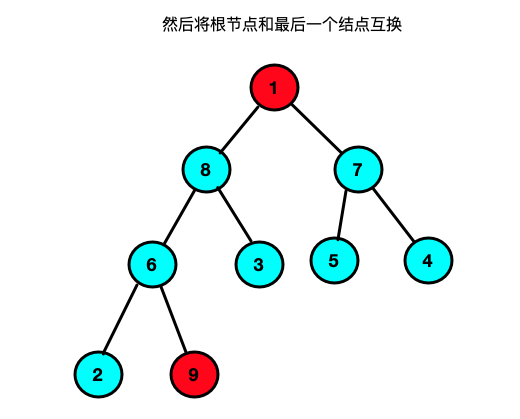
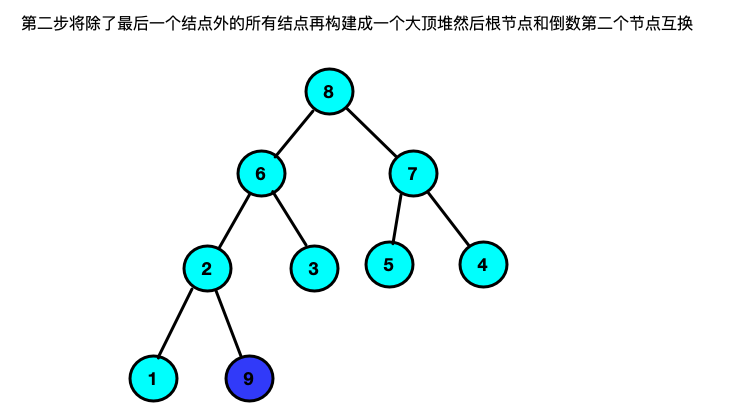
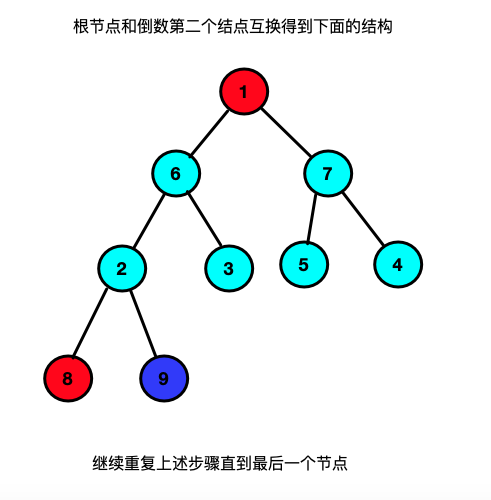
实现代码://大顶堆调整函数; /* 条件: 在list[s...m] 记录中除了下标s对应的关键字list[s]不符合大顶堆定义,其他均满足; 结果: 调整list[s]的关键字,使得list[s...m]这个范围内符合大顶堆定义. */ void HeapAjust(int *list,int s,int m){ int temp = list[s]; // int j = s; //当传入数组的最上限的二叉树发生变化,所以有可能接下来的二叉树不符合大顶堆的条件 //所以要for循环找到后面的所有子节点判断是否符合大顶堆条件不符合调整 for(int i = 2 * s + 1; i < m; i = 2*i +1){ if(i + 1 < m && list[i] < list[i + 1]) i++; if(list[i] < temp){ break; }else{ list[j] = list[i]; j = i; } } list[j] = temp; } //10.堆排序--对顺序表进行堆排序 void HeapSort(int *list,int size){ //1.将现在待排序的序列构建成一个大顶堆; //将L构建成一个大顶堆; //i为什么是从length/2.因为在对大顶堆的调整其实是对非叶子的根结点调整. for(int i = size/2-1; i >= 0; i --){ HeapAjust(list, i, size); } //每次循环将第一个元素和最后一个元素的内容进行替换 //(没替换一次最后一个元素就要减1) int temp; for(int i = 0; i < size; i ++){ temp = list[size - i - 1]; list[size - i - 1] = list[0]; list[0] = temp; //交换之后大顶堆可能被打乱所以重新整理使其重新满足大顶堆的条件 HeapAjust(list, 0, size - i - 1); } } -
归并排序
思路:其实就是将一组数据分成一个个小块进行排序之后再进行合并然后再排序 和希尔排序的区别是排序是间隔抽数据然后排序,同事希尔排序也没有合并的这一个操作
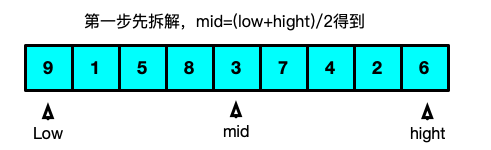
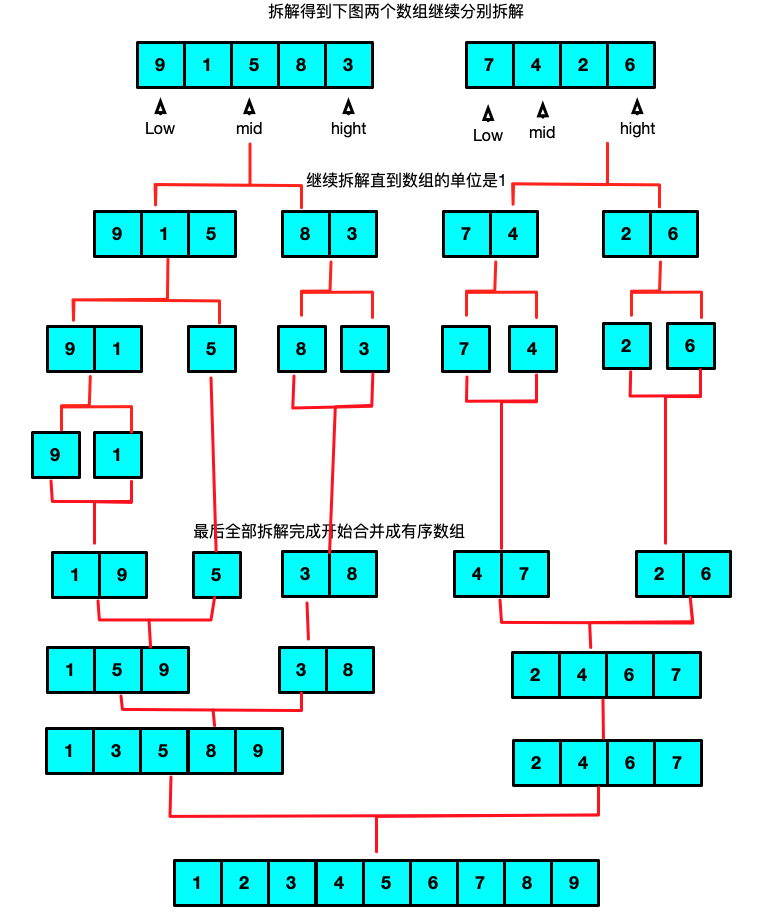
实现代码:/** 归并排序 实现思路:其实就是将一组数据分成一个个小块进行排序之后再进行合并然后再排序 和希尔排序的区别是排序是间隔抽数据然后排序,同事希尔排序也没有合并的这一个操作 */ //11.归并排序-对顺序表L进行归并排序 //(并不是将两个单独的数组合并成一个而是将一个数组的两段有序序列抽出合并成一个有序序列TR) //③ 将有序的SR[i..mid]和SR[mid+1..n]归并为有序的TR[i..n] void Merge(int SR[],int TR[],int i,int m,int n){ int k = 0,j = 0; //1.将SR中记录由小到大地并入TR for(j=m+1,k=i; i <= m && j <= n; k++){ if(SR[i] > SR[j]) TR[k] = SR[j ++]; else TR[k] = SR[i ++]; } //2.将剩余的SR[i..mid]复制到TR if(i <= m){ for(int l=0;l<=m-i;l++) TR[k+l]=SR[i+l]; } //3.将剩余的SR[j..mid]复制到TR if(j<=n) { for(int l=0;l<=n-j;l++) TR[k+l]=SR[j+l]; } } /** SR 待排序数组 TR1 最终被合并的数组 low 待分割数组的起始索引 hight 待分割数组的终点索引 */ Status MSort(int SR[],int TR1[],int low, int hight){ int mid; //中间分割点 int TR2[MAXSIZE]; //递归排序中用到传参 if(SR[low] == SR[hight]){ //说明分割区域只剩下一个数字了此时就赋值TR1 TR1[low] = SR[low]; }else{ //如果不是最后一个数字则继续分割 mid = (low + hight)/2; //应为分成了两段所以两段都需要继续分割 MSort(SR, TR2, low, mid); MSort(SR, TR2, mid + 1, hight); Merge(TR2, TR1, low, mid, hight); } return OK; } -
快速排序
思路:就是分治法,将一个数组拆分排序,每一次拆分都要保证右边的所有值一定大于左边的所有值,一直查分到只剩下两个元素的时候(也就是拆分出的数组只要起始索引小于终止索引则继续拆分)
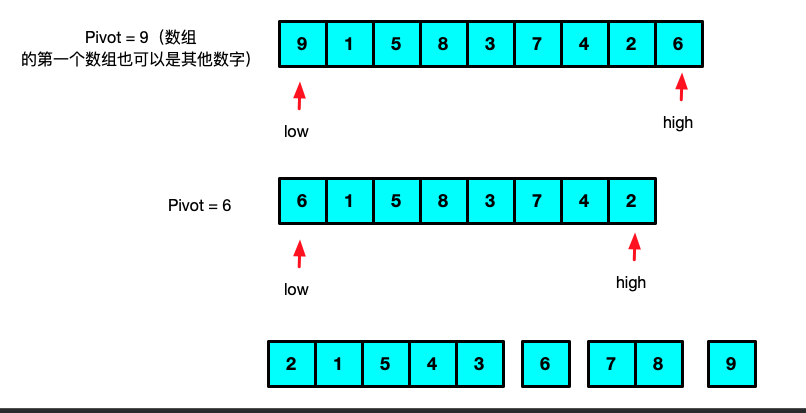
//13.快速排序-对顺序表L进行快速排序 /** 方法作用:将传入的数组用第一个数作为曲轴排列右边全部大于左边的数组 */ int Partition(int *list,int low,int high){ int pivotkey = list[low]; while (low < high) { while (low < high && list[high] >= pivotkey) { high --; } swap(list, low, high); while (low < high && list[low] <= pivotkey) { low ++; } swap(list, low, high); } print(list, 10); printf("\n"); return low; } //② 对顺序表L的子序列L->r[low,high]做快速排序; void QSort(int *list,int low,int high){ int n; if(low < high){ n = Partition(list,low,high); QSort(list, low, n-1); QSort(list, n + 1, high); }
}