from HihoCoder 1317 题解
描述
小Ho最近遇到一个难题,他需要解决一个棋局问题。
棋局分成了n行,m列,每行有若干个棋子。小Ho需要从中选择若干行使得每一列有且恰好只有一个棋子。
比如下面这样局面:
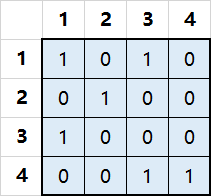
其中1表示放置有棋子的格子,0表示没有放置棋子。
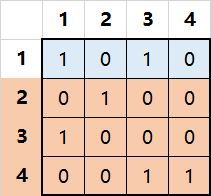
对于上面这个问题,小Ho经过多次尝试以后得到了解为选择2、3、4行就可以做到。
但是小Ho觉得自己的方法不是太好,于是他求助于小Hi。
小Hi:小Ho你是怎么做的呢?
小Ho:我想每一行都只有两种状态,选中和未被选中。那么我将选中视为1,未选中视为0。则每一种组合恰好对应了一个4位的01串,也就是一个4位的二进制数。
小Hi:恩,没错。
小Ho:然后我所做的就是去枚举每一个二进制数然后再来判定是否满足条件。
小Hi:小Ho你这个做法本身没什么问题,但是对于棋盘行数再多一点的情况就不行了。
小Ho:恩,我也这么觉得,那你有什么好方法么?
小Hi:我当然有了,你听我慢慢道来。
输入
第1行:1个正整数t,表示数据组数,1≤t≤10。
接下来t组数据,每组的格式为:
第1行:2个正整数n,m,表示输入数据的行数和列数。2≤n,m≤100。
第2..n+1行:每行m个数,只会出现0或1。
输出
第1..t行:第i行表示第i组数据是否存在解,若存在输出"Yes",否则输出"No"。
DLX模板题,代码:
// @Team : nupt2017team12
// @Author : Zst
// item url: http://hihocoder.com/problemset/problem/1317
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <vector>
#include <cmath>
#include <algorithm>
#include <map>
using namespace std;
#define LL long long
#define MOD 1000000007
#define CLR(a,x) memset(a,x,sizeof(a))
#define INF 0x3f3f3f3f
#define pb push_back
#define FOR(i,a,b) for( int i = ( a ); i <= ( b ); ++i )
#define WHILE() int T;scanf( "%d", &T );while( T-- )
const int N = 100+7;
int n, m;
bool ans;
int size;
const int NN = N + N * N;
int S[N], H[N];
int Col[NN], Row[NN];
int L[NN], R[NN], U[NN], D[NN];
void init() {
FOR( i, 0, m ) {
R[i] = i+1;
L[i] = i-1;
U[i] = i;
D[i] = i;
S[i] = 0;
}
R[m] = 0;
L[0] = m;
size = m;
FOR( i, 0, n ) {
H[i] = -1;
}
}
void link( int r, int c ) {
// cout<<r<<" "<<c<<endl;
size += 1;
Col[size] = c;
Row[size] = r;
D[size] = c;
U[size] = U[c];
D[U[c]] = size;
U[c] = size;
if( H[r] == -1 ) {
H[r] = size;
L[size] = size;
R[size] = size;
} else {
R[size] = H[r];
L[size] = L[H[r]];
R[L[H[r]]] = size;
L[H[r]] = size;
}
S[c] += 1;
}
void remove( int c ) {
R[L[c]] = R[c];
L[R[c]] = L[c];
for( int i = D[c]; i != c; i = D[i] ) {
for( int j = R[i]; j != i; j = R[j] ) {
D[U[j]] = D[j];
U[D[j]] = U[j];
S[Col[j]] -= 1;
}
}
}
void resume( int c ) {
for( int i = U[c]; i != c; i = U[i] ) {
for( int j = L[i]; j != i; j = L[j] ) {
D[U[j]] = j;
U[D[j]] = j;
S[Col[j]] += 1;
}
}
L[R[c]] = c;
R[L[c]] = c;
}
bool dance( int d ) {
if( R[0] == 0 ) {
ans = true;
return true;
}
int c = R[0];
// FOR( i, 1, m ) {
// cout<<S[i]<<endl;
// }
for( int i = R[c]; i != 0; i = R[i] ) {
// cout<<i<<endl;
if( S[i] < S[c] ) {
c = i;
}
}
// cout<<c<<endl;
// cout<<"debug"<<endl;
remove( c );
for( int i = D[c]; i != c; i = D[i] ) {
// cout<<i<<endl;
for( int j = R[i]; j != i; j = R[j] ) {
remove( Col[j] );
}
if( dance( d+1 ) ) {
return true;
}
for( int j = L[i]; j != i; j = L[j] ) {
resume( Col[j] );
}
}
resume( c );
return false;
}
int main()
{
// freopen( "1317.in", "r", stdin );
WHILE() {
ans = false;
scanf( "%d%d", &n, &m );
init();
FOR( i, 1, n ) {
FOR( j, 1, m ) {
int _a;
scanf( "%d", &_a );
if( _a == 1 ) {
link( i, j );
}
}
}
dance( 0 );
if( ans ) {
printf( "Yes\n");
} else {
printf( "No\n");
}
}
return 0;
}