from Towards Logical Specification of Statistical Machine Learning

Content

Preliminaries

前导知识，没怎么看懂，不过好像不影响后面
Techniques for Conditional Indistinguishability
- Counterfactual Epistemic Operators
  
  介绍了两个操作符，主要为形式化公平这个属性做准备
- Conditional Indistinguishability via Counterfactual Knowledge
  
  如何用上文描述的两个操作符去表示'Conditional Indistinguishability'
Formal Model for Statistical Classification
- Statistical Classification Problems
  
  给出了一些定义:
  - $C: D \rightarrow L$ , L be a finite set of class labels, D be the finite set of input data (called feature vectors) that we want to classify.
  - $f: D \times L \rightarrow R$ : be a scoring function that gives a score f(v, ℓ) of predicting the class of an input datum (feature vector) v as a label ℓ.
  - $H(v) = l$ : to represent that a label ℓ maximizes f(v, ℓ).
- Modeling the Behaviours of Classifiers
  
  给出了两个公式
  
  $\begin{array}{ll}{s |= \psi(x, y)} & {\text { iff } C\left(\sigma_{s}(x)\right)=\sigma_{s}(y)} \\ {s |= h(x, y)} & {\text { iff } H\left(\sigma_{s}(x)\right)=\sigma_{s}(y)}\end{array}$
  
  ψ(x, y) to represent that C classifies a given input x as a class y.
  
  h(x, y) to represent that y is the actual class of an input x.
Formalizing the Classification Performance
- 形式化 correctness
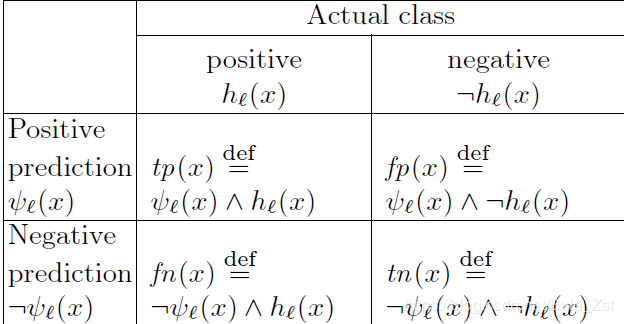
- true positive: $s |= \psi_{\ell}(x) \wedge h_{\ell}(x)$ .
- the precision being within an interval I is given by:
  
  $\operatorname{Pr}\left[v \stackrel{\$}{\leftarrow} \sigma_{w_{\mathrm{real}}}(x) : H(v)=\ell | C(v)=\ell\right] \in I$ or $\operatorname{Pr}\left[s \stackrel{\$}{\leftarrow} w_{\mathrm{real}} : s|=h_{\ell}(x) \ | \ s |= \psi_{\ell}(x)\right] \in I$ .
- $\text {Precisione}_{\ell, I}(x) \stackrel{\text { def }}{=} \psi_{\ell}(x) \supset \mathbb{P}_{I} h_{\ell}(x)$ and $\text { precision }=\frac{t p}{t p+f p}$ .
- $\operatorname{Recall}_{\ell, I}(x) \stackrel{\text { def }}{=} h_{\ell}(x) \supset \mathbb{P}_{I} \psi_{\ell}(x)$ and $\text {recall}=\frac{t p}{t p+f n}$ .
- $\begin{array}{l}{\text{Accuracy}_{\ell, I}(x) \stackrel{\text { def }}{=}} {\mathbb{P}_{I}(\operatorname{tp}(x) \vee \operatorname{tn}(x))}\end{array}$ and $\frac{T P+T N}{T P+T N+F P+F N}$ .
Formalizing the Robustness of Classifiers
- Probabilistic Robustness against Targeted Attacks
  - 定义：When a robustness attack aims at misclassifying an input as a specific target label, then it is called a targeted attack.
  - $\mathrm{K}_{\varepsilon}^{D} \varphi$ represents that the classifier C is confident that ϕ is true as far as it classifies the test data that are perturbed by a level ε of noise.
  - D defined by $D\left(\sigma_{w}(x) \| \sigma_{w^{\prime}}(x)\right)=\max _{v, v^{\prime}}\left\|v-v^{\prime}\right\|_{p}$ where v and v′ range over the datasets supp(σw(x)) and supp(σw′ (x)) respectively.
  - 以下是给出的公式：
  - $h_{\text {panda }}(x) \supset K_{\varepsilon}^{D} \mathbb{P}_{0} \psi_{\text {gibon }}(x)$ , which represents that a panda’s photo x will not be recognized as a gibbon at all after the photo is perturbed by noise.
  - $\text { Target Robust}_{panda, \delta}(x, \text { gibbon }) \stackrel{\text { def }}{=} K_{\varepsilon}^{D}\left(h_{\text {panda }}(x) \supset \mathbb{P}_{[0, \delta]} \psi_{\text {gibbon }}(x)\right)$ .
- Probabilistic Robustness against Non-Targeted Attacks
  - $\text { TotalRobust}_{\ell, I}(x) \stackrel{\text { def }}{=} K_{\varepsilon}^{D}\left(h_{\ell}(x) \supset \mathbb{P}_{I} \psi_{\ell}(x)\right)=K_{\varepsilon}^{D} \operatorname{Recall}_{\ell, I}(x)$ .
  - 结论：
  - $\text { TotalRobust}_{panda,I}(x) \text { implies TargetRobust }_{\text {panda }, \delta}(x, \text { gibbon })$ .
  - robustness can be regarded as recall in the presence of perturbed noise.
Formalizing the Fairness of Classifiers
- 符号定义
  - $s |= \eta_{G}(x) \text { iff } \sigma_{s}(x) \in G$ .
  - $w|=\xi_{d} \text { iff } \sigma_{w}(x)=d$ .
- Group Fairness (Statistical Parity)
  - 定义：the property that the output distributions of the classifier are identical for different groups.
  - $\mathcal{R}_{\varepsilon} \stackrel{\text { def }}{=}\left\{\left(w, w^{\prime}\right) \in \mathcal{W} \times \mathcal{W} | D\left(\sigma_{w}(y) \| \sigma_{w^{\prime}}(y)\right) \leq \varepsilon\right\}$ .
  - $\mathfrak{M}, w=\overline{\mathrm{P}_{\varepsilon}} \varphi \text { iff there exists a } w^{\prime} \text { s.t. }\left(w, w^{\prime}\right) \notin \mathcal{R}_{\varepsilon} \text { and } \mathfrak{M}, w^{\prime} |= \varphi$ .
  - $\text { GrpFair }(x, y) \stackrel{\text { def }}{=}\left(\eta_{G_{0}}(x) \wedge \psi(x, y)\right) \supset \neg \overline{\operatorname{P}_\varepsilon ^{\mathrm{tv}}} \mathbb{P}_{1}\left(\xi_{d} \wedge \eta_{G_{1}}(x) \wedge \psi(x, y)\right)$ .
- Individual Fairness (as Lipschitz Property)
  - the property that the classifier outputs similar labels given similar inputs.
  - $\mathcal{R}_{\varepsilon}^{r, D} \stackrel{\text { def }}{=}\left\{\left(w, w^{\prime}\right) \in \mathcal{W} \times \mathcal{W} | \begin{array}{c}{v \in \operatorname{supp}\left(\sigma_{w}(x)\right), v^{\prime} \in \operatorname{supp}\left(\sigma_{w^{\prime}}(x)\right)} \\ {D\left(\sigma_{w}(y) \| \sigma_{w^{\prime}}(y)\right) \leq \varepsilon \cdot r\left(v, v^{\prime}\right)}\end{array}\right\}$ .
  - $\operatorname{lndFair}(x, y) \stackrel{\text { def }}{=} \psi(x, y) \supset \neg \overline{\mathrm{P}_{\varepsilon}^{r, D}} \mathbb{P}_{1}\left(\xi_{d} \wedge \psi(x, y)\right)$ .
- Equal Opportunity
  - the property that the recall (true positive rate) is the same for all the groups.
  - $\mathrm{EqOpp}(x) \stackrel{\text { def }}{=}\left(\eta_{G}(x) \wedge \psi(x, y)\right) \supset \neg\overline{\mathrm{P}_{0}^{\mathrm{tv}}} \mathbb{P}_{1}\left(\xi_{d} \wedge \neg \eta_{G}(x) \wedge \psi(x, y)\right)$ .