AES算法基本原理本文包含了用swift编写的， AES 算法的简单实现。源码地址 AES 是 Advanced Enc

AES算法基本原理

本文包含了用swift编写的， AES 算法的简单实现。源码地址

AES是什么

AES 是 Advanced Encryption Standard 的缩写，即 高级加密标准。在密码学中又称Rijndael加密法，是美国联邦政府采用的一种分组加密标准。

AES 是为了取代DES而诞生的加密标准。1997年1月2号，美国国家标准技术研究所宣布希望征集高级加密标准。经过五年的甄选流程，Rijndael算法最终获胜，并在2002年5月26日成为有效的标准。

Rijndael 算法与 AES 标准唯一的区别是，在 AES 的规格中，分组长度固定为 128 比特。而在 Rijndael 算法中，分组长度可以以32比特为单位在 128 比特到 256 比特的范围内选择。

根据密钥的长度不同，可分别称之为 AES-128 、 AES-192、 AES-256。他们的加密轮次也有所不同。

AES	密钥长度（Nk）	向量长度（IV）	分组大小（Nb）	加密轮数（Nr）	子密钥数
AES-128	16	16	16	10	11
AES-192	24	16	16	12	13
AES-256	32	16	16	14	15

生成子密钥的数量比AES算法的轮数多一个，因为第一个密钥加法层进行密钥漂白时也需要子密钥。

AES 的基本原理

总体结构

Rijndael算法是基于代换-置换网络（SPN，Substitution-permutation network）的迭代算法。明文数据经过多轮次的转换后方能生成密文，每个轮次的转换操作由轮函数定义。轮函数任务就是根据密钥编排序列（即轮密码）对数据进行不同的代换及置换等操作。

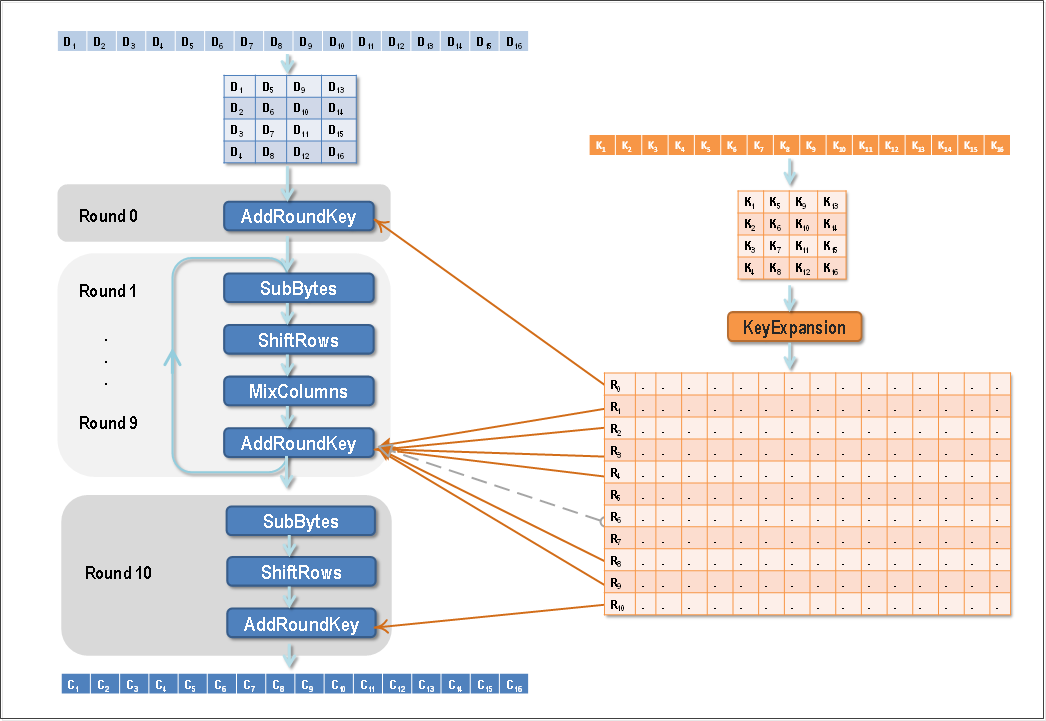
图左侧为轮函数的流程，主要包含4种主要运算操作：字节代换(SubByte)、行移位(ShiftRow)、列混合(MixColumn)、轮密钥加(AddRoundKey)。图右侧为密钥编排方案，在Rijndael中称为密钥扩展算法（KeyExpansion）。

初始状态（state）

在运算之前，我们需要把明文分组成 128 位每段进行分别处理。

对于段长 128 位的明文，需要以从上到下从左到右的次序，成一个 4x4 的矩阵（每个元素是一个字节），即初始状态（state）。

struct  Matrix {
    var content: [[UInt8]]
    init(data: [UInt8]) {
        var result = Array(repeating:Array(repeating:UInt8(0), count: 4), count: 4)
        for i in 0..<4 {
            for j in 0..<4 {
                let index = 4 * i + j
                result[i][j] = index < data.count ? data[index] : 0
            }
        }
        self.content = result
    }
}

值得注意的是，我们得到的是一个二维数组，而每一个字数组代表一列而不是一行。

为了查看效果，我们继承 CustomStringConvertible ，方便我们将计算结果打印出来。

extension Matrix : CustomStringConvertible {
    var description: String {
        var mstr = ""
        for i in 0..<4 {
            for j in 0..<4 {
                let data = self.content[j][i]
                mstr += String(format: "%2x ", data)
            }
            mstr += "\n"
        }
        return mstr
    }
}

子密钥生成

在进行运算之前，我们还需要对密钥进行处理，生成一组子密钥。并且进行每一轮加密的时候，会依次选用不同的子密钥。因而这一步所生成的密钥又叫做 轮密钥。

生成子密钥的算法叫做 密钥扩展算法（KeyExpansion）。它是 Rijndael 的密钥编排实现算法，其目的是根据种子密钥（用户密钥）生成多组轮密钥。

密钥生成的流程图如下：

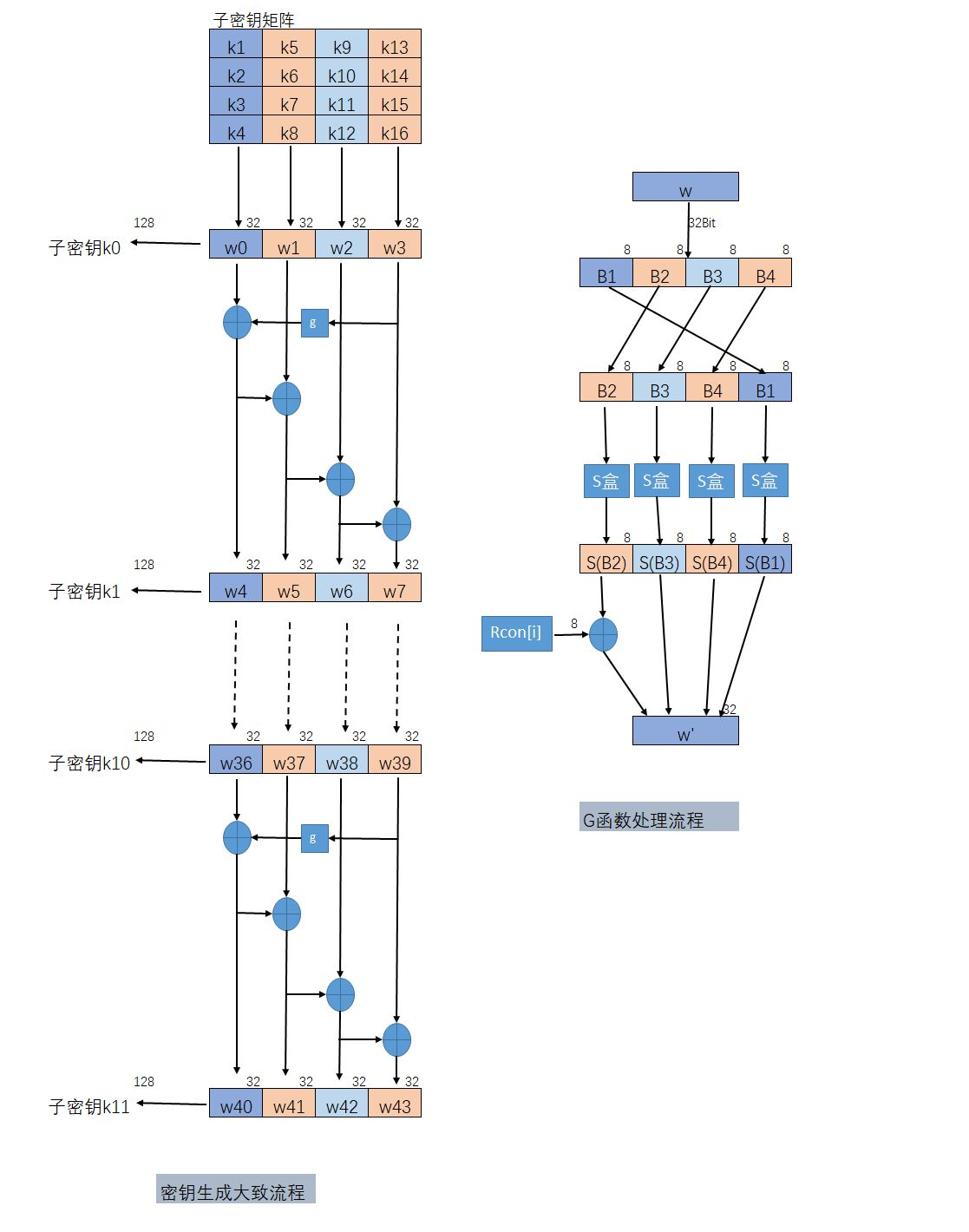
子密钥的生成是以列为单位进行的，一列是32Bit，四列组成子密钥共128Bit。生成子密钥的数量比AES算法的轮数多一个，因为第一个密钥加法层进行密钥漂白时也需要子密钥。密钥漂白是指在AES的输入盒输出中都使用的子密钥的XOR加法。子密钥在图中都存储在W[0]、W[1]、...、W[43]的扩展密钥数组之中。

首先我们需要将原始的密钥，生成一系列 32 比特，四个字节的 word。并且需要知道当前的密钥变换的轮次。

struct Word {
  
   private var content: [UInt8]
	
   init(_ content:[UInt8]) {
      self.content = content
  }
  
   init(value: UInt32) {
        let r0  = UInt8((value & 0xff000000) >> (3 * 8))
        let r1  = UInt8((value & 0xff0000)   >> (2 * 8))
        let r2  = UInt8((value & 0xff00)     >> (1 * 8))
        let r3  = UInt8(value & 0xff)
        self.init([r0,r1,r2,r3])
   }

    var value : UInt32 {
        var res : UInt32 = 0
        for i in 0..<4 {
            res += UInt32(self.content[i]) << ((4 - i - 1) * 8)
        }
        return res
    }
}

函数 G() 首先将4个输入字节进行翻转，并执行一个按字节的S盒代换，最后用第一个字节与轮系数Rcon进行异或运算。G()函数存在的目的有两个，一是增加密钥编排中的非线性；二是消除AES中的对称性。这两种属性都是抵抗某些分组密码攻击必要的。

轮系数 Rcon 是一个一维数组，一个元素1个字节。长度与子密钥个数相同，i 为进行密钥变换的轮次，也就是子密钥的下标。

// 轮系数
private let kRcon : [UInt8] = [ 0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36 ]

g 函数实现如下：

func g () {
  var buf = [content[2], content[3], content[4], content[1]]
  buf =  buf.map({ kSbox[Int($0)] })
  buf[0] ^= kRcon[self.round]
}

那么，生成论密钥实现如下：

static func keyExpansion(_ key: [UInt8]) -> [Matrix] {
    var roundKeys = [Matrix](repeating: Matrix.zero, count: Nr + 1)

    // The first round key is the key itself.
    roundKeys[0]  = Matrix(data: key)

    for round in 1...Nr {
        var words = roundKeys[round-1].words
        words[0] = words[3].g(round: round)  ^ words[0]
        words[1] = words[0] ^ words[1]
        words[2] = words[1] ^ words[2]
        words[3] = words[2] ^ words[3]
        roundKeys[round] = Matrix(words: words)
    }

    return roundKeys
}

轮函数

轮密钥加/密钥加法层

AddRoundKey

在密钥加法层中有两个输入的参数，分别是明文和子密钥k[0]，而且这两个输入都是128位的。k[0]实际上就等同于密钥k，具体原因在密钥生成中进行介绍。我们前面在介绍扩展域加减法中提到过，在扩展域中加减法操作和异或运算等价，所以这里的处理也就异常的简单了，只需要将两个输入的数据进行按字节异或操作就会得到运算的结果。

密钥加是将轮密钥简单地与状态 state 进行逐比异或。

private func addRoundKey (_ state:State,round: Int) -> State {
    return state ^ self.roundKeys[round]
}

其中，self.roundKeys 为之前生成的轮密钥。

两个矩阵的异或运算，即是两个矩阵中元素依次进行异或变换：

func ^ (rh: AESImpl.State,lh: AESImpl.State) -> AESImpl.State {
    return rh.xor(lh)
}

func xor (_ other: State) -> State {
    var result = [UInt8]()
    for i in 0..<16 {
        result.append( self.data[i]  ^ other.data[i] )
    }
    return State(result)
}

值得注意的是，AddRoundKey 没有逆运算，因为进行两次异或运算之后得到的是其本身。

字节代换

SubBytes

首先需要逐个字节将地对 16 字节的输入数据进行字节替换处理。也就是根据每个字节的值（16进制）为索引，从一个 16 * 16 的替换表 (S-Box) 中查找对应的值进行替换处理。

AES的 S-Box 如下：

行/列	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0x63	0x7c	0x77	0x7b	0xf2	0x6b	0x6f	0xc5	0x30	0x01	0x67	0x2b	0xfe	0xd7	0xab	0x76
1	0xca	0x82	0xc9	0x7d	0xfa	0x59	0x47	0xf0	0xad	0xd4	0xa2	0xaf	0x9c	0xa4	0x72	0xc0
2	0xb7	0xfd	0x93	0x26	0x36	0x3f	0xf7	0xcc	0x34	0xa5	0xe5	0xf1	0x71	0xd8	0x31	0x15
3	0x04	0xc7	0x23	0xc3	0x18	0x96	0x05	0x9a	0x07	0x12	0x80	0xe2	0xeb	0x27	0xb2	0x75
4	0x09	0x83	0x2c	0x1a	0x1b	0x6e	0x5a	0xa0	0x52	0x3b	0xd6	0xb3	0x29	0xe3	0x2f	0x84
5	0x53	0xd1	0x00	0xed	0x20	0xfc	0xb1	0x5b	0x6a	0xcb	0xbe	0x39	0x4a	0x4c	0x58	0xcf
6	0xd0	0xef	0xaa	0xfb	0x43	0x4d	0x33	0x85	0x45	0xf9	0x02	0x7f	0x50	0x3c	0x9f	0xa8
7	0x51	0xa3	0x40	0x8f	0x92	0x9d	0x38	0xf5	0xbc	0xb6	0xda	0x21	0x10	0xff	0xf3	0xd2
8	0xcd	0x0c	0x13	0xec	0x5f	0x97	0x44	0x17	0xc4	0xa7	0x7e	0x3d	0x64	0x5d	0x19	0x73
9	0x60	0x81	0x4f	0xdc	0x22	0x2a	0x90	0x88	0x46	0xee	0xb8	0x14	0xde	0x5e	0x0b	0xdb
A	0xe0	0x32	0x3a	0x0a	0x49	0x06	0x24	0x5c	0xc2	0xd3	0xac	0x62	0x91	0x95	0xe4	0x79
B	0xe7	0xc8	0x37	0x6d	0x8d	0xd5	0x4e	0xa9	0x6c	0x56	0xf4	0xea	0x65	0x7a	0xae	0x08
C	0xba	0x78	0x25	0x2e	0x1c	0xa6	0xb4	0xc6	0xe8	0xdd	0x74	0x1f	0x4b	0xbd	0x8b	0x8a
D	0x70	0x3e	0xb5	0x66	0x48	0x03	0xf6	0x0e	0x61	0x35	0x57	0xb9	0x86	0xc1	0x1d	0x9e
E	0xe1	0xf8	0x98	0x11	0x69	0xd9	0x8e	0x94	0x9b	0x1e	0x87	0xe9	0xce	0x55	0x28	0xdf
F	0x8c	0xa1	0x89	0x0d	0xbf	0xe6	0x42	0x68	0x41	0x99	0x2d	0x0f	0xb0	0x54	0xbb	0x16

实现起来很简单

func subBytes(datas: [UInt8]) -> [UInt8]
{
    var result = [UInt8]()
    for (index,data) in datas.enumerated() {
        result[index] = kSbox[Int(data)]
    }
    return result
}

InvSubBytes

逆字节代换也就是查逆S盒来变换，逆S盒如下：

行/列	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0x52	0x09	0x6a	0xd5	0x30	0x36	0xa5	0x38	0xbf	0x40	0xa3	0x9e	0x81	0xf3	0xd7	0xfb
1	0x7c	0xe3	0x39	0x82	0x9b	0x2f	0xff	0x87	0x34	0x8e	0x43	0x44	0xc4	0xde	0xe9	0xcb
2	0x54	0x7b	0x94	0x32	0xa6	0xc2	0x23	0x3d	0xee	0x4c	0x95	0x0b	0x42	0xfa	0xc3	0x4e
3	0x08	0x2e	0xa1	0x66	0x28	0xd9	0x24	0xb2	0x76	0x5b	0xa2	0x49	0x6d	0x8b	0xd1	0x25
4	0x72	0xf8	0xf6	0x64	0x86	0x68	0x98	0x16	0xd4	0xa4	0x5c	0xcc	0x5d	0x65	0xb6	0x92
5	0x6c	0x70	0x48	0x50	0xfd	0xed	0xb9	0xda	0x5e	0x15	0x46	0x57	0xa7	0x8d	0x9d	0x84
6	0x90	0xd8	0xab	0x00	0x8c	0xbc	0xd3	0x0a	0xf7	0xe4	0x58	0x05	0xb8	0xb3	0x45	0x06
7	0xd0	0x2c	0x1e	0x8f	0xca	0x3f	0x0f	0x02	0xc1	0xaf	0xbd	0x03	0x01	0x13	0x8a	0x6b
8	0x3a	0x91	0x11	0x41	0x4f	0x67	0xdc	0xea	0x97	0xf2	0xcf	0xce	0xf0	0xb4	0xe6	0x73
9	0x96	0xac	0x74	0x22	0xe7	0xad	0x35	0x85	0xe2	0xf9	0x37	0xe8	0x1c	0x75	0xdf	0x6e
A	0x47	0xf1	0x1a	0x71	0x1d	0x29	0xc5	0x89	0x6f	0xb7	0x62	0x0e	0xaa	0x18	0xbe	0x1b
B	0xfc	0x56	0x3e	0x4b	0xc6	0xd2	0x79	0x20	0x9a	0xdb	0xc0	0xfe	0x78	0xcd	0x5a	0xf4
C	0x1f	0xdd	0xa8	0x33	0x88	0x07	0xc7	0x31	0xb1	0x12	0x10	0x59	0x27	0x80	0xec	0x5f
D	0x60	0x51	0x7f	0xa9	0x19	0xb5	0x4a	0x0d	0x2d	0xe5	0x7a	0x9f	0x93	0xc9	0x9c	0xef
E	0xa0	0xe0	0x3b	0x4d	0xae	0x2a	0xf5	0xb0	0xc8	0xeb	0xbb	0x3c	0x83	0x53	0x99	0x61
F	0x17	0x2b	0x04	0x7e	0xba	0x77	0xd6	0x26	0xe1	0x69	0x14	0x63	0x55	0x21	0x0c	0x7d

实现起来也很简单

func invSubBytes(datas: [UInt8]) -> [UInt8]
{
    var result = [UInt8]()
    for (index,data) in datas.enumerated() {
        result[index] = kInvSBox[Int(data)]
    }
    return result
}

行位移

ShiftRows

行位移操作最为简单，只需将矩阵的字节进行位置上的置换。ShiftRows 子层属于 AES 手动的扩散层，目的是将单个位上的变换扩散到影响整个状态当中，从而达到雪崩效应。

在加密时，保持矩阵的第一行不变，第二行向左移动8Bit(一个字节)、第三行向左移动2个字节、第四行向左移动3个字节。

static func shiftRows (_ state: Matrix) {

    var temp : UInt8 = 0

    // Rotate first row 1 columns to left
    temp         = state[0][1]
    state[0][1]  = state[1][1]
    state[1][1]  = state[2][1]
    state[2][1]  = state[3][1]
    state[3][1]  = temp

    // Rotate second row 2 columns to left
    let temp0    = state[0][2]
    let temp1    = state[1][2]
    state[0][2]  = state[2][2]
    state[1][2]  = state[3][2]
    state[2][2]  = temp0
    state[3][2]  = temp1

    // Rotate third row 3 columns to left
    temp         = state[0][3]
    state[0][3]  = state[3][3]
    state[3][3]  = state[2][3]
    state[2][3]  = state[1][3]
    state[1][3]  = temp
}

InvShiftRows

解密时只需要按照相反的方向移动字节就可以了

static func shiftRows (_ state: Matrix) {

    var temp : UInt8 = 0

    // Rotate first row 1 columns to right
    temp         = state[0][1]
    state[0][1]  = state[3][1]
    state[3][1]  = state[2][1]
    state[2][1]  = state[1][1]
    state[1][1]  = temp

    // Rotate second row 2 columns to right
    let temp0    = state[0][2]
    let temp1    = state[1][2]
    state[0][2]  = state[2][2]
    state[1][2]  = state[3][2]
    state[2][2]  = temp0
    state[3][2]  = temp1

    // Rotate third row 3 columns to right
    temp         = state[0][3]
    state[0][3]  = state[1][3]
    state[1][3]  = state[2][3]
    state[2][3]  = state[3][3]
    state[3][3]  = temp
}

#####列混淆

列混淆子层是AES算法中最为复杂的部分，属于扩散层，列混淆操作是AES算法中主要的扩散元素，它混淆了输入矩阵的每一列，使输入的每个字节都会影响到4个输出字节。行位移子层和列混淆子层的组合使得经过三轮处理以后，矩阵的每个字节都依赖于16个明文字节成可能。其中包含了矩阵乘法、伽罗瓦域内加法和乘法的相关知识。

MixColumns

列混合变换是通过矩阵相乘来实现的，经行移位后的状态矩阵与固定的矩阵相乘，得到混淆后的状态矩阵，如下图的公式所示：

状态矩阵中的第j列(0 ≤j≤3)的列混合可以表示为下图所示：

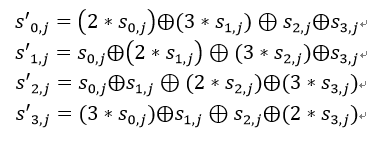
其中，矩阵元素的乘法和加法都是定义在基于GF(2^8)上的二元运算,并不是通常意义上的乘法和加法。这里涉及到一些信息安全上的数学知识，不过不懂这些知识也行。其实这种二元运算的加法等价于两个字节的异或，乘法则复杂一点。对于一个8位的二进制数来说，使用域上的乘法乘以(00000010)等价于左移1位(低位补0)后，再根据情况同(00011011)进行异或运算，设S1 = (a7 a6 a5 a4 a3 a2 a1 a0)，刚0x02 * S1如下图所示：

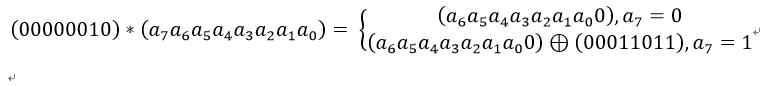
也就是说，如果a7为1，则进行异或运算，否则不进行。类似地，乘以(00000100)可以拆分成两次乘以(00000010)的运算：

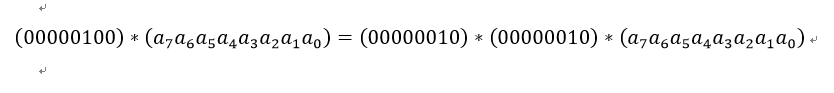
乘以(0000 0011)可以拆分成先分别乘以(0000 0001)和(0000 0010)，再将两个乘积异或：

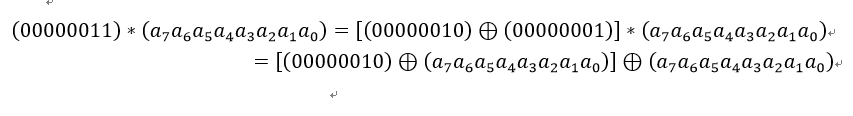
具体实现为：

static func mixColumns (_ state: Matrix) {
    var t    : UInt8 = 0
    var Temp : UInt8 = 0
    var Tm   : UInt8 = 0

    for i in 0..<4 {
        t            = state[i][0]
        Temp         = state[i][0] ^ state[i][1] ^ state[i][2] ^ state[i][3]

        Tm           = state[i][0] ^ state[i][1]
        Tm           = xtime(Tm)
        state[i][0]  ^= Tm ^ Temp

        Tm           = state[i][1] ^ state[i][2]
        Tm           = xtime(Tm)
        state[i][1]  ^= Tm ^ Temp

        Tm           = state[i][2] ^ state[i][3]
        Tm           = xtime(Tm)
        state[i][2]  ^= Tm ^ Temp

        Tm           = state[i][3] ^ t
        Tm           = xtime(Tm)
        state[i][3]  ^= Tm ^ Temp
    }
}

其中 xtime 函数为

static func xtime (_ x: UInt8) -> UInt8 {
    return ((x<<1) ^ (((x>>7) & 1) * 0x1b));
}

InvMixColumns

逆向列混合变换可由下图的矩阵乘法定义：

可以验证，逆变换矩阵同正变换矩阵的乘积恰好为单位矩阵。

具体实现为：

static func invMixColumns (_ state: Matrix) {
    for i in 0..<4 {
        let a = state[i][0]
        let b = state[i][1]
        let c = state[i][2]
        let d = state[i][3]

        state[i][0]  = multiply(a, 0x0e) ^ multiply(b, 0x0b) ^ multiply(c, 0x0d) ^ multiply(d, 0x09)
        state[i][1]  = multiply(a, 0x09) ^ multiply(b, 0x0e) ^ multiply(c, 0x0b) ^ multiply(d, 0x0d)
        state[i][2]  = multiply(a, 0x0d) ^ multiply(b, 0x09) ^ multiply(c, 0x0e) ^ multiply(d, 0x0b)
        state[i][3]  = multiply(a, 0x0b) ^ multiply(b, 0x0d) ^ multiply(c, 0x09) ^ multiply(d, 0x0e)
    }
}

其中，multiply 乘法运算为：

static func multiply (_ x: UInt8,_ y: UInt8) -> UInt8 {
    var result =   (y & 1) * x
        result ^=  (y>>1 & 1) * xtime(x)
        result ^=  (y>>2 & 1) * xtime(xtime(x))
        result ^=  (y>>3 & 1) * xtime(xtime(xtime(x)))
        result ^=  (y>>4 & 1) * xtime(xtime(xtime(xtime(x))))
   return result
}

AES算法基本原理