[博客迁移][题解] HDU 5791在网上搜了一些题解，都说这题很简单，然后一言不合就贴代码，可能我太菜了吧，想了好久

from HDU 5791 题解

在网上搜了一些题解，都说这题很简单，然后一言不合就贴代码，可能我太菜了吧，想了好久，在这里说一下比较详细的思路。

题目链接：acm.hdu.edu.cn/showproblem…

题目大意：给A、B两个序列，问相同子序列的个数

方法：dp

公式：

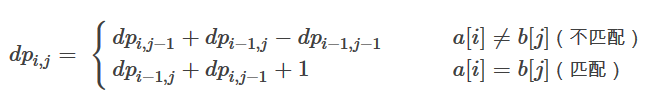
举例解释：

对于 A: 1,2,3,4 B: 1,2,3 这两个序列

他们的子序列分别是：

对于每一个序列，第一行是去掉最后一个数字形成的新序列（如，对于A来说，就是1 2 3）的子序列，第二行是第一行的序列加上最后一个数字

A、B相同的子序列的个数就是将第三行的子序列分别和第一行第二行的子序列相比，再加上第四行的子序列和第一行第二行的子序列相比

用数学公式表示就是： 1-3 2-3 1-4 2-4

其中，1-3与1-4的和就是1 2 3这个序列（A序列去掉最后的那个数字）和1 2 3这个序列（B序列）的相同子序列的个数

同理，B序列去掉最后一个数字与 A序列的相同子序列的个数就是1-3与2-3的和

为了表述，记A-1表示A序列去掉最后一个数字形成的新序列聪明的你一定会发现，如果把A-1与B的结果和A与B-1的结果相加，会多出1-3，而1-3表示的就是A-1与B-1的结果，这就是公式里面减去 $dp_{i-1,j-1}$ 的原因。

最后，还有2-4没有算，这里分两种情况

如果A序列最后一个数字与B序列最后一个数字不相等，那么2-4的答案一定是0，为什么呢？因为它们最后一个数字始终不相等哇！
如果最后一个数字相等，那么2-4的结果就等于1-3的结果再加1，为什么呢？因为，第二行是第一行的序列再加上A的最后一个数字，第四行是第三行的序列再加上B的最后一个数字。而多的那个1则是因为最后一个数字会单独形成一个新的序列。之前减去的1-3，现在又加回来了，所以公式里面，当不相等的时候，就只加了一个1。

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<vector>
#include<cmath>
#include<algorithm>
#include<map>
using namespace std;
#define ll long long

const int N = 1000000007;
const int M = 1005;
ll ans[M][M];
int l, s;
int lstr[M];
int sstr[M];

void func()
{
    memset( ans, 0, sizeof( ans ) );
    for( int i = 1; i <= l; i++ ) {
        for( int j = 1; j <= s; j++ ) {
            ans[i][j] = ( ans[i][j-1] + ans[i-1][j] - ans[i-1][j-1] + N ) % N;
            if( lstr[i] == sstr[j] ) {
                ans[i][j] += ans[i-1][j-1] + 1;
                ans[i][j] %= N;
            }
        }
    }
    printf( "%lld\n", ans[l][s] );
}

int main()
{
    #ifdef LOCAL
        freopen( "J.txt", "r", stdin );
    #endif
    while( ~scanf( "%d%d", &l, &s ) ) {
        memset( lstr, 0, sizeof( lstr ) );
        memset( sstr, 0, sizeof( sstr ) );

        for( int i = 1; i <= l; i++ ) {
            scanf( "%d", lstr + i );
        }
        for( int i = 1; i <= s; i++ ) {
            scanf( "%d", sstr + i );
        }
        func();
    }
    return 0;
}