二叉搜索树的最近公共祖先

要求：给定一个二叉搜索树，找到该树中两个指定节点的最近公共祖先。

案例：

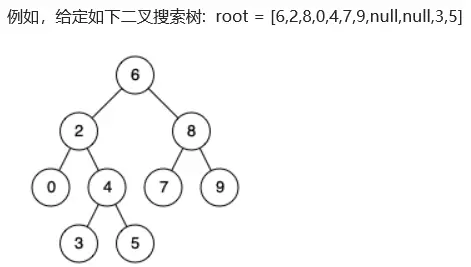
输入：root=[6,2,8,0,4,7,9,null,null,3,5], p=2, q=8
输出：6

输入：root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出：2

思路：

1. 抓住二叉搜索树的特性，左子树的值小于根节点，根节点的值小于右子树的值
2. 什么情况下，root为p，q的最近公共祖先：

• p,q在root的异侧
• p=root,q在root的左右子树中
• q=root,p在root的左右子树中

3. 所以使用迭代，判断条件是root==null时跳出。
4. p,q不变，移动root去判断。例如如果都在左子树，那么root就移动到root的左子节点上，再去进行判断。

代码：

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) {val = x;}
}

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        while (root != null) {
            if (root.val < p.val && root.val < q.val) {
                root = root.right;
            } else if (root.val > p.val && root.val > q.val) {
                root = root.left;
            } else break;
        }
        return root;
    }
}

二叉树的最近公共先祖

要求：给定一个二叉树，找到该树中两个指定节点的最近公共祖先。

案例；

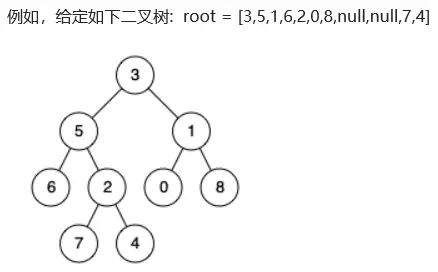
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5

思路：

1. 二叉树不同于二叉搜索树，根节点和左右子树的节点的值是没有明显的逻辑关系的。
2. root是p,q的最近公共祖先的情况：

• p,q分列在root两侧
• p=root，q在root的左右子树中
• q=root，p在root的左右子树中

3. 使用递归：

• 终止条件：

•   1. 越过叶子节点，返回null 
    2. root=p,q，返回root
  

• 递推工作：

•   1. 递推左子树，返回left 
    2. 递推右子树，返回right
  

• 返回值：

•   1. 左右均为null,返回null
    2. 左右均不为空，分列在root的两侧，返回root
    3. 左侧left为空，右侧right不为空：说明p或q在right中，返回right
    4. left不为空，右侧right为空：说明p或q在left中，返回left
  

4. 其实就是一个递归，返回的根节点的值根据左右递归返回的值来确定。左右均为空，返回空；左右均不为空，均有值返回，说明这个节点就是那个要找的祖先节点；左为空，右不为空，说明，返回的就是右，因为p,q均在右子树中。

代码：

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q) return root;
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if (left == null && right == null) return null;
        if (left == null) return right;
        if (right == null) return left;
        return root;
    }
}