介绍:
本篇用大白话来实现树的遍历,相信看完后“妈妈再也不用担心我的学习啦“!
最近在力扣上刷算法题,觉得这么多年都白混了(啥也没记录下来)。
名词解释:
树的遍历方式总体分为两类:
DFS: 深度优先搜索(depth first search)
BFS: 广度优先搜索(breadth-first search)
shift() 方法用于把数组的第一个元素从其中删除,并返回第一个元素的值。
unshift() 方法可向数组的开头添加一个或更多元素,并返回新的长度。
定义树
假设有如下结构类型的树,我们先来定义下该树,每个节点有三个属性(值,左节点,有节点)
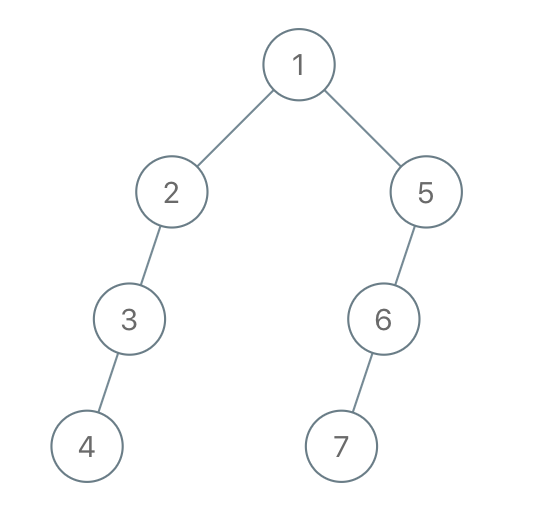
// 定义树let root = { "val":"1", "left":{ "val":"2", "left":{ "val":"3", "left":{ "val":"4", "left":null, "right":null }, "right":null } }, "right":{ "val":"5", "left":{ "val":"6", "left":{ "val":"7", "left":null, "right":null }, "right":null }, "right":null }}; BFS: 广度优先
期望输出:['1', '2', '5', '3', '6', '4', '7']
思路: 借助队列(先进先出)数据结构,这里按照实现步骤描述:
1. 第一层: 定义一个数组(queue)将根节点push进去,此时queue长度为1;
2. 第二层: 读取队列的第一个节点(此时为根节点1,shift方法取第一个元素并从原数组中移除)的左节点和右节点,依次push到数组中,此时数组长度为2,节点为【2, 3】,此时读取的是树的第二层节点;
3. 第三层 :再取队列的第一个节点(此时为节点为2,shift方法取第一个元素并从原数组中移除)的左节点和右节点,依次push到队列数组中此时队列中为【3,4,5】;
下一步该读取3的左右节点并push到队列中,移除第一个节点【节点3】队列变为【4,5,6,7】,均为第三层的节点;
第三层遍历完成,数组中全部是第三层的叶子节点;
4. 扩展:如果有更多层,则循环执行及实现整棵树的遍历;
代码: 为嘛变一行了😢
let BFS = function(tree) { // 队列 let queue = []; //存放遍历的节点值 let stack = []; // 第一步,将根节点放入队列中 queue.push(tree) while (queue.length > 0) { // 队列中的第一个节点 let firstNodeInQueue = queue.shift(); stack.push(firstNodeInQueue.val); // 取左节点 push到队列中 firstNodeInQueue.left && queue.push(firstNodeInQueue.left); // 取右节点 push到队列中 firstNodeInQueue.right && queue.push(firstNodeInQueue.right); } return stack;}
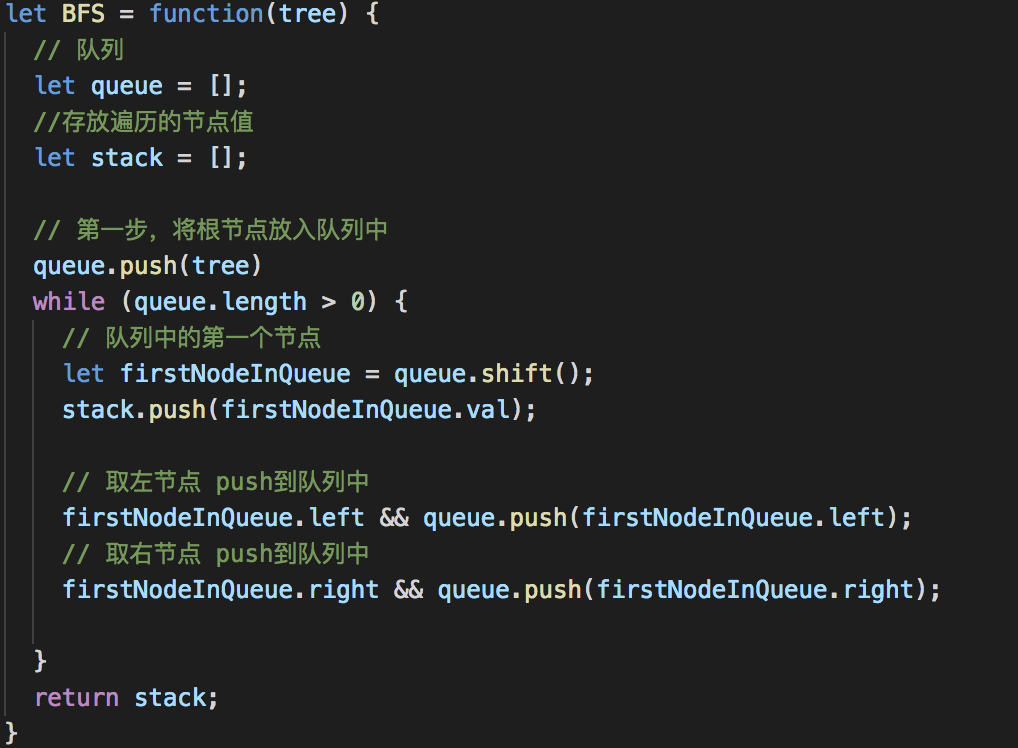
DFS: 深度优先
期望输出:['1', '2', '3', '4', '5', '6', '7']
思路:两种方案,数组方式和递归方式
数组方式: 同广度遍历,借助数组队列来实现
1. 将根节点push到队列中, 此时queue长度为1【1】;
2. 读取queque的第一个节点(shift方法)的右节点和左节点,依次 放入队列的开始位置(先右节点,再左节点)。执行完第一次循环后,队列变为【2,5】,第二次循环后,变为【3,5】,第四次循环后变为【4,5】,第五次循环变为【5】,第六次变为【6】,第七次变为【7】然后结束;
递归方式:如果左节点存在,循环调用遍历方法; 然后再判断右节点是否存在,再循环调用自身;
代码:为嘛变一行了😢
let DFS = function (root) { let queue = []; let stack = [];
// 栈方式 queue.push(root); while(queue.length>0) { let firstNode = queue.shift(); stack.push(firstNode.val); firstNode.right&& queue.unshift(firstNode.right) firstNode.left && queue.unshift(firstNode.left); } // 递归方法 // const travers = function(tree) { // stack.push(tree.val); // tree.left && travers(tree.left) // tree.right && travers(tree.right) // } // travers(root) return stack;}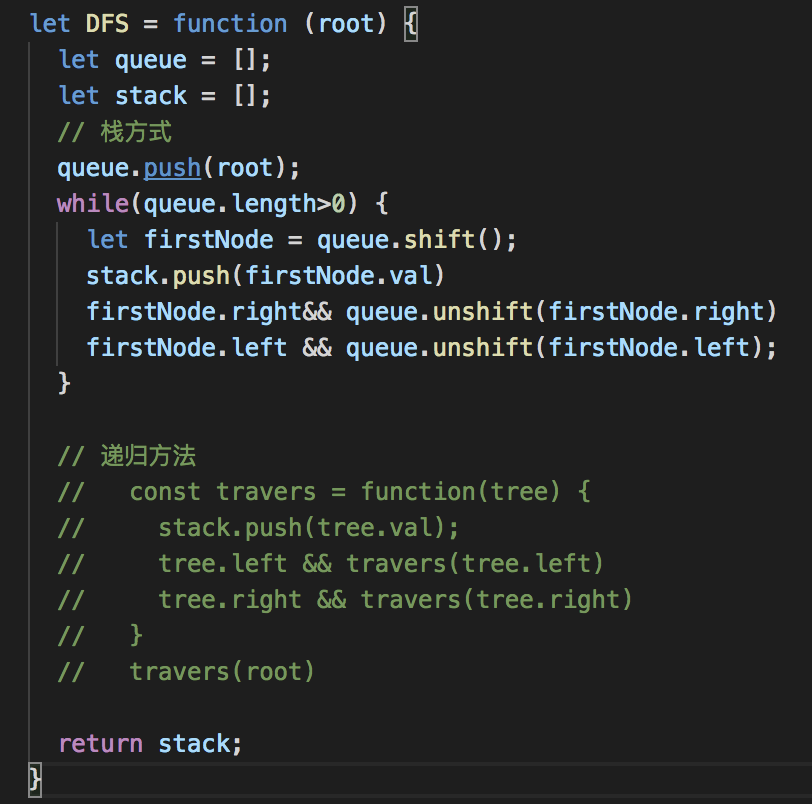
结语:
用最直白的话来记录BFS和DFS, 刚开始可能觉得有点绕,难以理解,建议先用在纸上画图,用自己的话描述出来,再去实现代码,顿时觉得脑子够用了哈哈, 欢迎大家共同探讨!