最近对一些二进制位有些许想法,写了一点二进制的整理,肯定是不全的...作为美好的开始,我觉得还是可以的...

二进制

在我们日常生活中,我们所受的教育是以十进制为基础(毕竟十个手指头嘛),但其实数是可以是任意进制的.在计算机中,是以一串高或低的电信号来体现的,因此,计算机只用2个字母来表示,也就是0和1,所以我们通常认为计算机语言就是二进制数.

所有信息都由二进制数位或位(bit)组成.因此二进制数的基本运算单位是bit,取值可以是高或低,开或关,0或1,真或假.

1. 二进制转十进制

把一个二进制转为十进制公式:

d代表每位的值,而Base则表示的是数的基数是什么,如果为二进制就是2,十六进制就是16,而i就表示该位从右向左数属于第几位(从0开始),该方法同样适用于其他进制.

例如以下二进制数转为十进制的公式位

在一个二进制数中:110111,从右向左依次标记位:0,1,2,3,4...将第0位标识为最低有效位,也就是最右边的那位,将第5位标识位最高有效位,即最左边的一位.

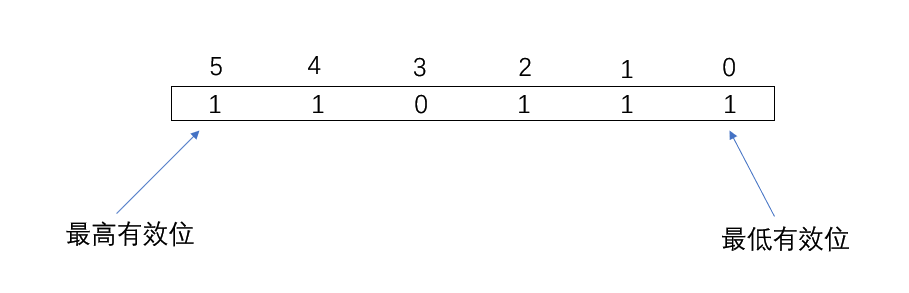
上面是二进制数的一般表现形式,事实上二进制数可以由无穷多的位组成,只是除了最右边的几位数,其余的都补0.

清楚了上面这些,我们硬件可以对二进制数进行加,减,乘,除操作,如果操作结果不能被硬件所表示,就发生了溢出,而如何处理溢出是由编程语言和,操作系统,程序所决定的.

计算机需要对正数和负数进行操作,需要一种方法以便于区分正数和负数,先想到的肯定是通过添加一个符号位的方式进行添加.但是这种方法有明显的缺点:

最终的解决方案是选择一种易于硬件实现的表达方式:前导位为0表示正数,前导位为1表示负数.这种表示方式称为: 二进制补码.

这也同样带来了个问题,二进制补码中的最小负数没有相应的正数与之对应,这种问题也会给粗心的程序员带来烦恼,但相比其他方法,不会给硬件和程序设计人员造成困扰.因此,现在所有计算机都采用二进制补码的方式来表示有符号数.

二进制补码优点在于:硬件只需监测最高有效位的值,便知道是正数还是负数(0为正,1为负).因此最高有效位也叫符号位.计算二进制转换的方式也需要发生变化:

只需要将符号位的计算变成乘于负数即可.

同样,二进制补码数也可能会发生操作数溢出,这种溢出的情况发生在一个有限位的二进制数的符号位和一个无穷多位的数左边的值不一样的情况下.

对一个二进制补码数进行取反的快速方法就是,对每一位取反,1变0,0变1.然后对结果进行加1.这种方法的基于这样一个事实:一个数和他按位取反的结果相加一定是1111...1111也就是-1,得出公式:

把一个n位表示的数转为一个多于n位表示的数,也有一种快速的方法,例如把二进制补码表示的16位值,添加到一个32位的容器中.这个时候就只需要将16位值复制到32位的低16中,其余的高16位则用最高有效位进行填充.这种方式通常叫做符号扩展.

其实二进制补码数在左侧有无限多的最高有效位数,只是为了适应硬件的宽度,数的前导位被隐藏了,符号扩展只是还原了一部分.

在程序世界里,避免不了对二进制数进行操作.像常见的移位,与,或...等等.

移位

移位应该是用得较多的了,有左移,右移等,他们将所有位数都向左或者向右移动,在空出来的位置填零.例如:

0000 0000 0000 1100 = 12 左移4位: 0000 0000 1100 0000 = 192

与之对应的还有右移,这两种移位准确来说是逻辑左移和右移,这种移位还有个好处,就是往左移i位就是2i,就相当于十进制数往左移i位就等于乘以10i,例如上面的左移四位就相当于乘以2的4次方(16),原12,而12x16对于192.

按位与

按位与即当两个操作数都为1时,结果才为1:

值1: 0000 0000 0011 0101

值2：0000 0000 0011 1010
 
按位与结果:0000 0000 0011 0000

按位与提供了将某些位置变为0的能力,前提是另一个对应的操作位的值为0,后一个操作数被称为:掩码.

按位或

与按位与对应的就是按位或,他的要求是两个操作位中有一个为1,结果就为1:

值1: 0000 0000 0011 0101

值2：0000 0000 0011 1010

按位或结果:0000 0000 0011 1111

除了上面这些操作外,还有

以上整理的一些二进制的知识点,虽然不全,但我觉得作为一个起点或许会不错!