一、回溯思想简介
回溯的处理思想,有点类似枚举搜索。我们枚举所有的解,找到满足期望的解。为了有规律地枚举所有可能的解,避免遗漏和重复,我们把问题求解的过程分为多个阶段。每个阶段,我们都会面对一个岔路口,我们先随意选一条路走,当发现这条路走不通的时候(不符合期望的解),就回退到上一个岔路口,另选一种走法继续走。
解决一个回溯问题,实际上就是一个决策树的遍历过程,一般来说我们需要解决三个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
回溯算法模板:在递归之前做选择,在递归之后撤销选择
function backtrack (路径,选择列表){
if(满足结束条件){
result.add(结果);
}
for(选择:选择列表){
做出选择;
backtrack(路径,选择列表);
撤销选择;
}
}
二、剪枝
上面说到回溯算法就像一颗N叉树,底下有很多的子节点(树枝),比如我们将一个数组从小到大排序后,第二个数已经大于要求的结果,那么它后面的数一定也大于要求结果,所以没必要再往下进行遍历,直接剪掉这个枝(跳出循环),进行下一轮搜索。所以一般回溯算法离不开剪枝,搜索问题一般复杂度较高,能剪枝就尽量需要剪枝。把候选数组排个序。
三、例题解释
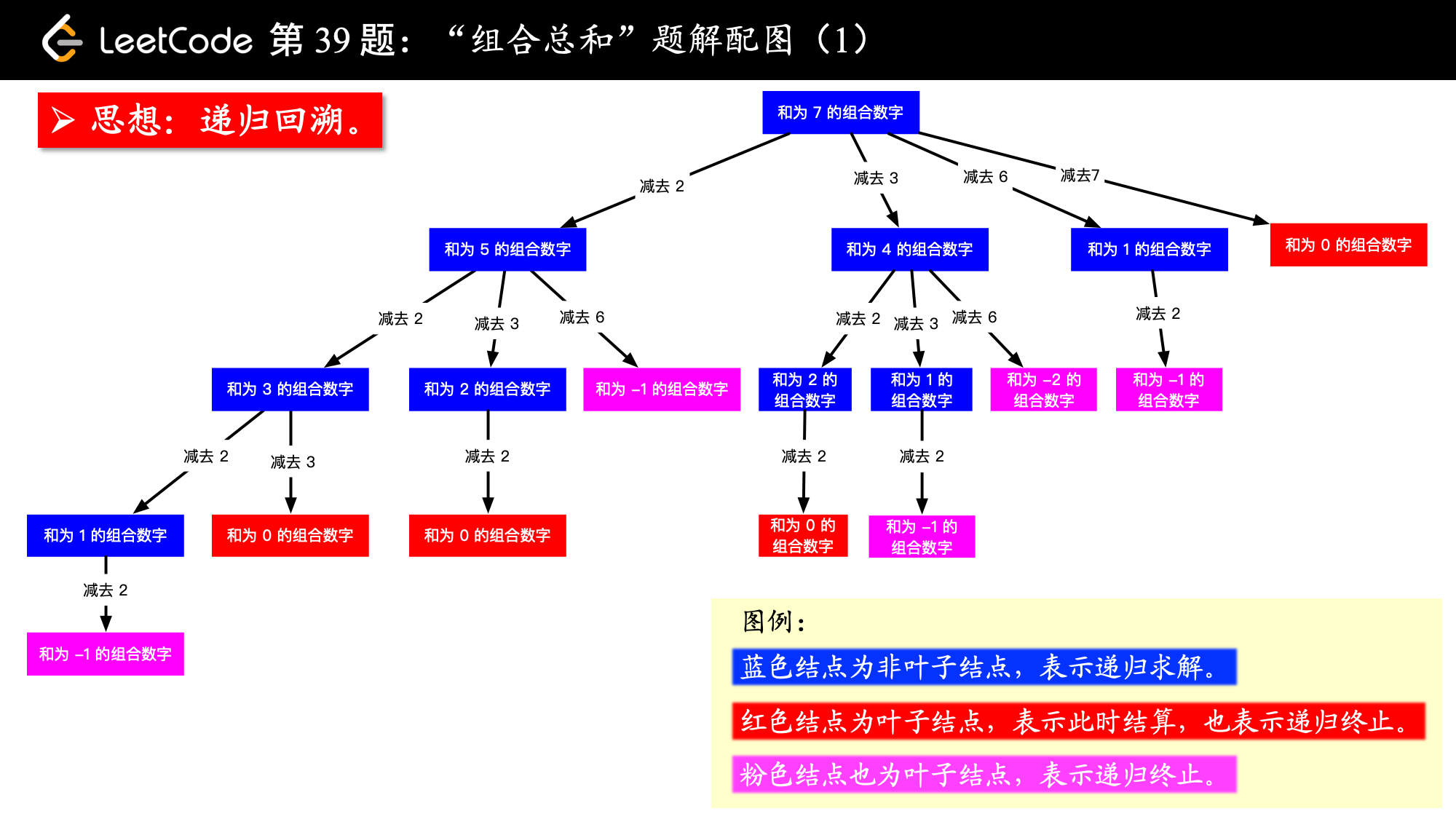
39、组合总和
思路:
由题意可知:原数组元素不重复,寻找一个符合条件的组合 且原数组的单个元素可以重复使用
只要结果中的子组合互不相同即可
题解:
且原数组的单个元素可以重复使用:a、意味着下一个for循环中的元素选取,要从前一个元素开始,因为可以重复使用,不然如果跟着for的自增变量i走,会漏掉可能解 b、将自增变量i传递下去
终止条件:target 一一减去符合组合的元素,最终为 0 ,才是一个符合题意的组合
/**
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
var combinationSum = function(candidates, target) {
let n = candidates.length;
let res = [];
let temp = [];
candidates = candidates.sort((a, b) => a - b); // 先从小到大排序
let help = (temp, target, start) => {
if (target === 0) { // 终止条件
res.push(temp);
return;
}
for (let i = start; i < n; i++) {
if (target < candidates[i]) break; // 剪枝操作
temp.push(candidates[i]);
help(temp.slice(),target - candidates[i],i);
temp.pop(); // 撤销选择
}
}
help(temp, target, 0);
return res;
};
40、组合总和II
对于本题来说,它相对于39. 组合总和的不同之处在于数组 candidates会存在相同的数字,如果存在相同的数字,我们就可能会出一下重复的组合,例如:

首先,第一个操作
之前选择过的不用再去选择 这说明第一次我们的选择列表是**[1,2,2,2,5],那第二次我们的选择列表就应该是[2,2,2,5]**。
第二个操作为:
如果以当前结点为头结点的所有组合都找完了,那么下一个与他他相同的头结点就不用去找了。
/**
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
var combinationSum2 = function(candidates, target) {
let n = candidates.length;
let res = [];
let temp = [];
candidates = candidates.sort((a, b) => a - b);
function help(temp, target, start) {
if(target === 0){
res.push(temp);
return;
}
for (let i = start; i < n; i ++) {
if(target < candidates[i]) break; // 剪枝操作
if(i > start && candidates[i-1] === candidates[i]) continue; // 当前元素不能重复使用
temp.push(candidates[i]);
help(temp.slice(),target - candidates[i],i + 1); // 区别:进行+1
temp.pop();
}
}
help(temp, target, 0);
return res;
};
46、全排列
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permute = function(nums) {
const res = [];
const paths = [];
function backtrack(paths, selections) {
if (paths.length === nums.length) {
res.push(paths.slice());
return
}
for (let selection of selections) {
// 组合和全排列的区别是遇到当前已有的continue进行下一个循环
if (paths.includes(selection)) continue;
paths.push(selection);
backtrack(paths, selections);
paths.pop();
}
}
backtrack(paths, nums);
return res;
};
51、N皇后
这是一道比较经典的回溯 + 剪枝操作的题目,已经出现在字节跳动和腾讯的面试中,下面介绍下思路:
循环扫荡每一行,然后遍历每一列,要满足同一列,撇,捺方向上没有皇后,满足条件就给数组第n行push一个列的位置,生成一个[1, 3, 0, 2]这样一个皇后位置的数组,最后用'.'和'Q'填充成一个二维数组。
这里一个难点是怎么判断列、撇、捺上面有没有放置皇后,通过观察我们可以发现列直接判断纵坐标的点是否相等就可以。
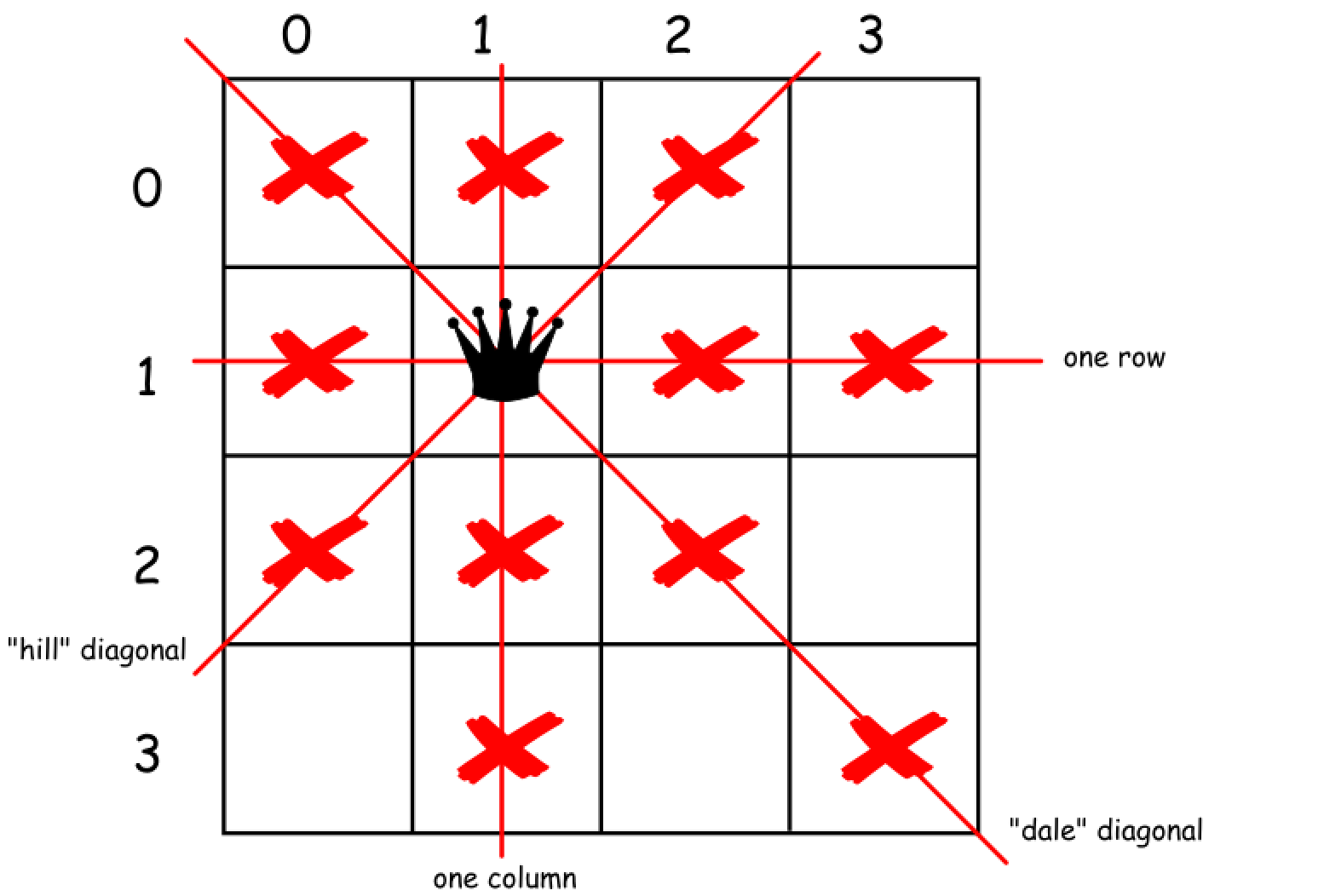
捺上的皇后满足:x1 - x2 = y1 - y2这样的规律。
/**
* @param {number} n
* @return {string[][]}
*/
var solveNQueens = function(n) {
// 回溯 + 剪枝
let res = [];
dfs();
function dfs(sub = [], row = 0) {
if (row === n) {
// sub: [1, 3, 0 2]
res.push(sub.map(i => '.'.repeat(i) + 'Q' + '.'.repeat(n - i - 1)));
}
// 遍历每一行
for (let i = 0; i < n; i++) {
// 坐标点为(row, i)表示这个点是否可以放皇后
// v: 列,j: 行
// sub里面是皇后的坐标 sub: [1, 3, 0 2]
if (!sub.some((v, j) => (
// 列
v === i
// 撇
|| row - v === j - i
// 捺
|| j - row === v - i))) {
sub.push(i);
dfs(sub, row + 1);
sub.pop();
}
}
}
return res;
};
以上就是回溯算法的简单介绍了,大家多进行一些定向练习:回溯算法