Deep Boosting for Image Denoising

2020-06-12 252 阅读2分钟

ECCV 2018

Chang Chen，Zhiwei Xiong，Xinmei Tian, Feng Wu

简介

文章使用了基于boosting的多轮迭代去雾算法，并在此基础上迭代联合训练，其网络权重并未共享。

Motivation

Boosting去噪背景知识

去噪问题的目标是从 $y\in \mathbb{R}^{N\times M}$ 中恢复 $x\in \mathbb{R}^{N\times M}$ ， $y\in \mathbb{R}^{N\times M}$ 用公式可以表达为：

y=x+v \tag{1}

其中 $v$ 表示服从高斯分布的噪声。而去噪可以表达为：

\hat{x}=\mathcal{S}(y)=\mathcal{S}(x+v) \tag{2}

其中 $\mathcal{S}(\cdot)$ 表示普通的去噪方法， $\hat{x}$ 表示 $x$ 的近似。由于算法不是完美的，因此 $\hat{x}$ 也不能完全等于 $x$ ，它们之间的差距可以表达为：

u=\hat{x}-x=v_r-x_r \tag{3}

其中 $x_r$ 表示未恢复的图像（信号）， $v_r$ 表示 $\hat{x}$ 中剩余的噪声。换句话说， $\hat{x}$ 减去剩余的噪声 $v_r$ 加上未恢复的图像（信号） $x_r$ 就能得到完全恢复的图像。

有一种将boosting算法应用于去噪的简单想法是，从残差中迭代提取未恢复的图像（信号） $x_r$ 再加回 $\hat{x}$ ：

\hat{x}^{n+1}=\hat{x}^n+\mathcal{H}(y-\hat{x}^n) \tag{4}

其中 $\mathcal{H}(\cdot)$ 是迭代提取符号，并将 $\hat{x}^0$ 设置为0。但注意到，残差 $y-\hat{x}$ 不仅包含一部分未恢复的图像（信号） $x_r$ ,还包含一部分噪声：

y-\hat{x}=(x+v)-(x+u)=(x+v)-(x+v_r+x_r)=x_r+(v-v_r) \tag{5}

很自然的，能够出现另外一个想法，迭代去噪图像结果 $\hat{x}$ 来消除残留的噪声 $v_r$ :

\hat{x}^{n+1}=\mathcal{F}(\hat{x}^n) \tag{6}

其中 $\mathcal{F}(\cdot)$ 代表某降噪模型。但是由于它忽略了包含大多数高频信息的 $x_r$ ，而会导致过度平滑。

为了进一步提高Boosting框架的性能，Romano和Elad提出了一种SOS算法。每个迭代步骤中的降噪目标是增强图像 $y+\hat{x}^n$ ，而不是增强残差 $y-\hat{x}^n$ 或者 $\hat{x}^n$ ，但是为了保证SOS的可迭代性，它必须在每个步骤中减去相同的 $\hat{x}^n$ :

\hat{x}^{n+1}=\mathcal{G}(y+\hat{x}^{n})-\hat{x}^{n} \tag{7}

其中 $\mathcal{G}(\cdot)$ 是一种降噪模型。进一步说，可以将 $y+\hat{x}$ 分解为：

y+\hat{x}=(x+v)+(x+u)=2x+(v+u) \tag{8}

假设 $||u||=\delta||v||$ ， $\delta\ll1$ 。根据Cauchy-Schwarz不等式，可以得到 $SNR(y+\hat{x})>SNR(y)$ 。

其中，公式（7）中，为了维护SOS的可迭代性，减去了 $\hat{x}^n$ ，但在深度学习中，可以在没有这种约束下学习：

\hat{x}^n=\mathcal{G}_{\theta_n}\{y+\mathcal{G}_{\theta_{n-1}}[y+\cdot\cdot\cdot \mathcal{G}_{\theta_2}(y+\mathcal{G}_{\theta_1}(y))\cdot\cdot\cdot]\} \tag{9}

Model

文章通过实验发现从PN-DN-DDN-DDFN的过程中，网络逐步提高了学习能力。在这之中拓展了深度，短连接，扩张卷积，路径拓展融合等。

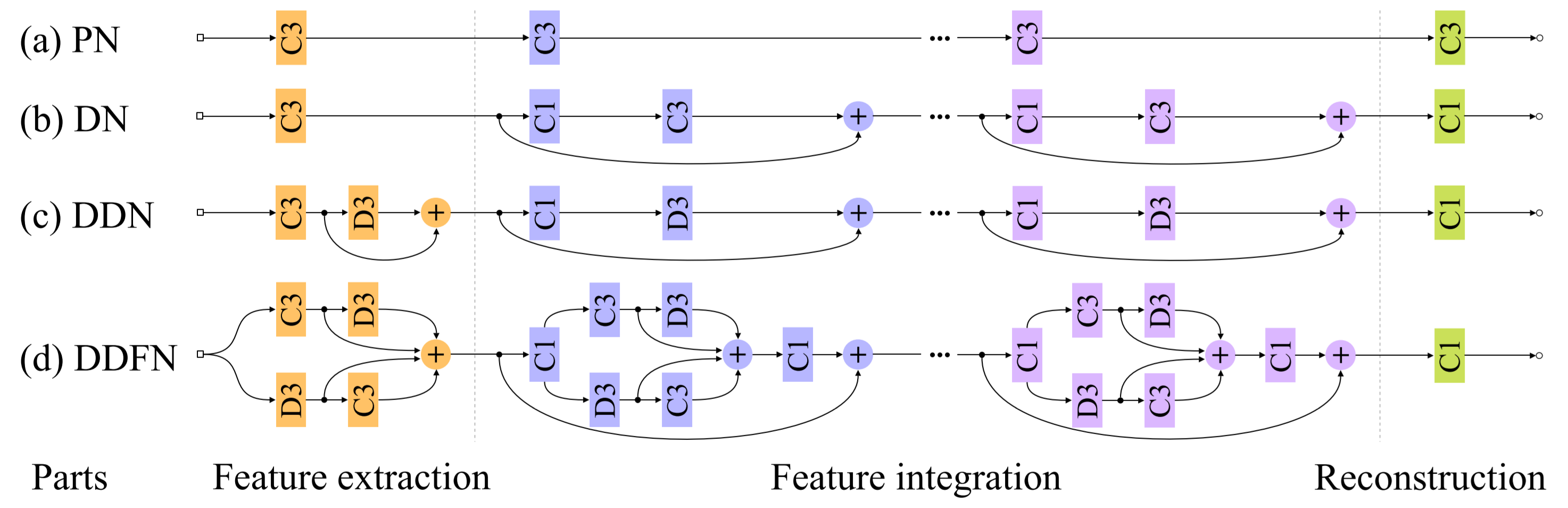
上图展示的网络结构为公式(9)中的一个去噪步骤，并非全部。

对比和测试

结果展示