关系代数

一、概述

1.关系代数

关系代数一种抽象的查询语言，是关系数据操纵语言的一种传统表达方式。它是用对系的运算来表达查询的。

2.关系代数运算的三个要素

运算对象：关系
运算结果：关系
运算符：四类运算符

关系运算符有四类：集合运算符，专门的关系运算符，算术比较符、逻辑运算符，如下表所示：

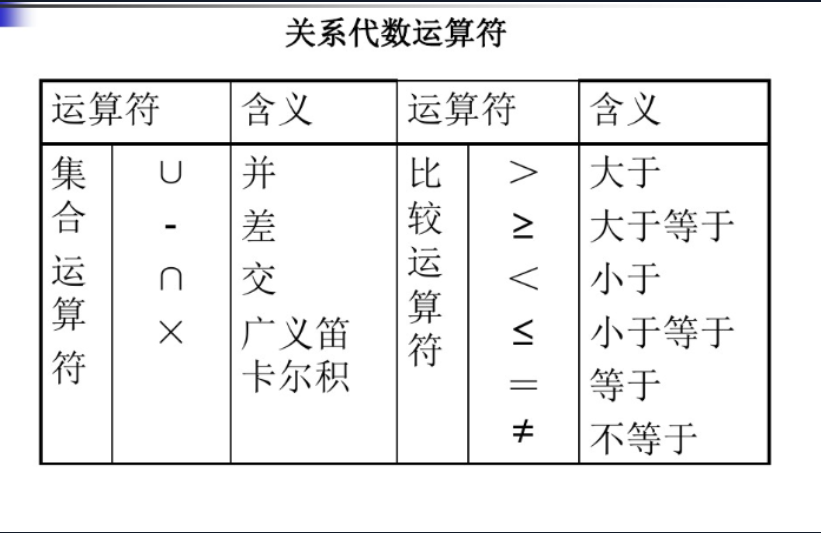
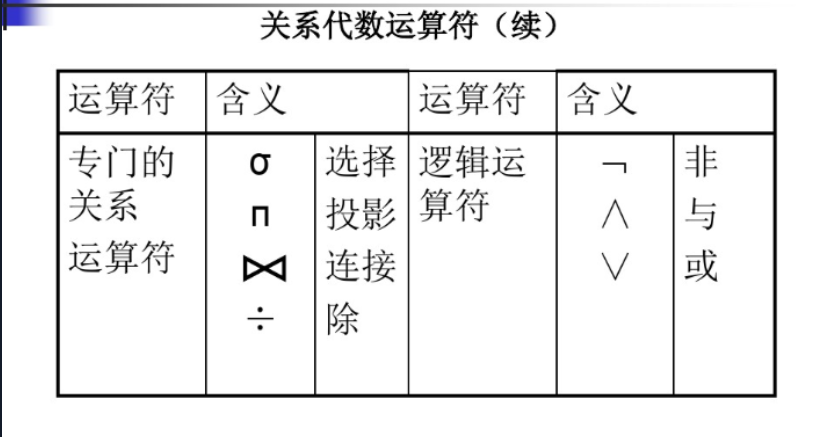
集合运算符
- 将关系看成元组的集合
- 运算是从关系的“水平”方向，也就是“行”的角度来进行。
专门的关系运算符
- 不仅涉及行，而且涉及列
算数比较符号
- 辅助专门的关系运算符进行操作
逻辑运算符
- 辅助专门的关系运算符进行操作

3.关系代数运算分类

传统的集合运算

并、差、交、广义笛卡尔积

专门的关系运算

选择、投影、连接、除

4.关系代数的表示记号

R：设关系模式为R (A ₁，A ₂，....，A _n)，它的一个关系设为R。
t ∈ R：表示 t 是 R 的一个元组(一行)
t [A _i ]：表示元组 t 中相应于 A _i 的一个分量

二、传统的关系运算

1.并（Union）

1.1 R 和 S 的性质

具有相同的目 n （即两个关系都有 n 个属性）
相应的属性取自同一个域（R和S具有相同的关系模型）

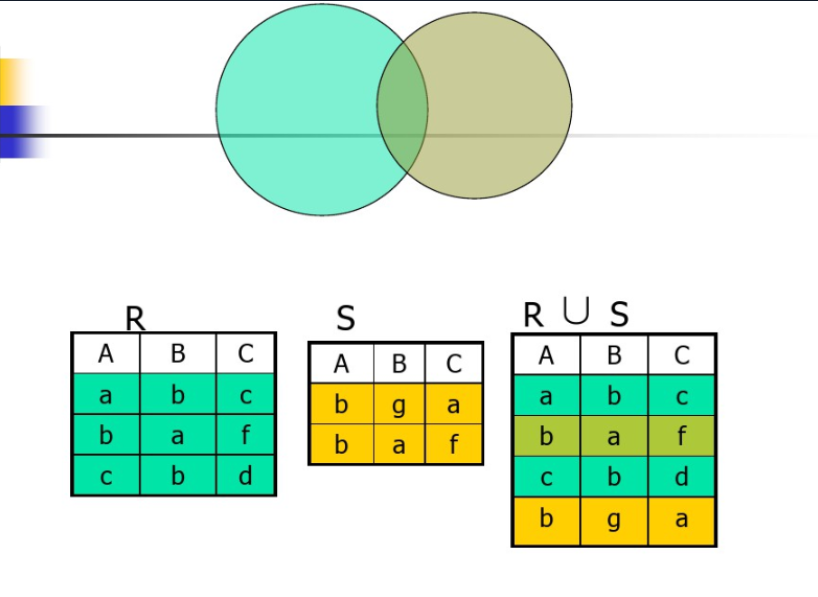
1.2 R ∪ S

仍为 n 目关系，由属于R或属于S的元组组成

R ∪ S = { t | t ∈ R V t ∈ S}

2.差（Difference）

2.1 R 和 S 的性质

具有相同的目 n （即两个关系都有 n 个属性）
相应的属性取自同一个域（R和S具有相同的关系模型）

2.2 R - S

仍为 n 目关系，由属于R而不属于S的所有元组组成

3.交（Intersection）

3.1 R 和 S 的性质

具有相同的目 n （即两个关系都有 n 个属性）
相应的属性取自同一个域（R和S具有相同的关系模型）

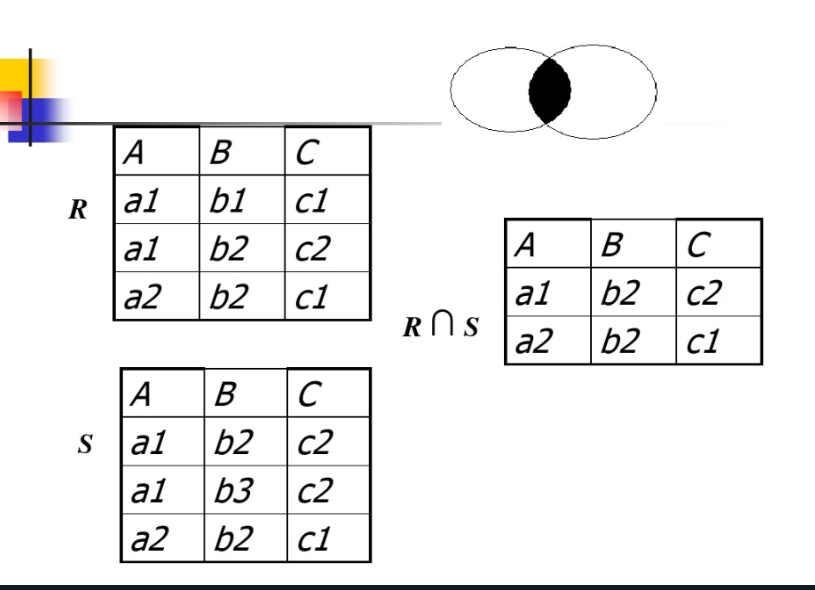
3.2 R ∩ S

仍为 n 目关系，由既属于R又属于S的元组组成

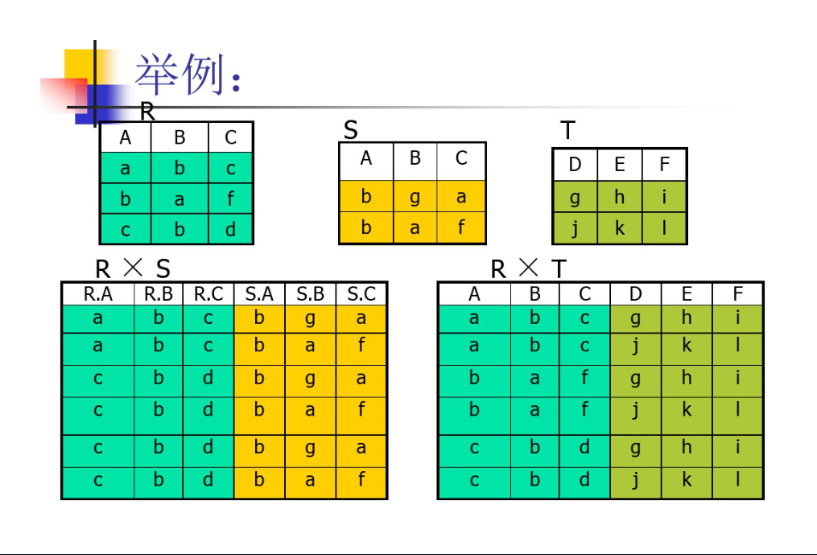
4.广义笛卡尔积（Extend Cartesian Produint）

4.1 R的性质

n 目关系，k ₁ 个元组

4.2 S的性质

m 目关系，k ₂ 个元组

4.3 R × S

列：( n + m) 列的元组的集合
- 元组的前 n 列是关系 R 的一个元组
- 后 m 列是关系 S 的一个元组
行：K₁ × K₂ 个元组

三、专门的关系运算

选择
投影
连接
除

1. 选择（Selection）

选择又称为限制（Restriction）

1.1 选择运算符的含义：

在关系R中选择满足给定条件的诸元组 σ_F(R) = { t | t ∈ R ∧ F (t) = '真' }

选出满足给定谓词的元组，用“σ”符号表示，而将谓词写作σ的下标，参数关系在 σ 后的括号中。

举例：选择关系instructor中属于“物理(Physics)”系的那些元组，可以用关系代数：σ_{dept_name}=_"Physics"(instructor)来进行选择。

通常，我们允许在选择谓词中进行比较，使用的是， =，≠，<，>。我们也可以使用连词and(Λ), or(ν), 和not(¬)将多个谓词合并为一个较大的谓词。

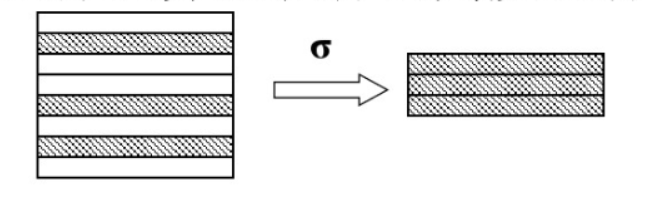
1.2 选择运算是从行的角度进行的运算

2.投影（Projection）

列举所有我们希望在结果中出现的属性，用"π"符号表示，而将我们想要的属性作为下标，作为参数的关系紧跟在 π 后的括号中。

例，可以通过如下关系代数来获得上述的教师列表：
π _{ID,name,salary}(instructor)。

2.1 投影运算符的含义

从 R 中选择出若干属性列组成新的关系：π_A(R) = { t[A] | t ∈ R } （A是R中的属性）

例子：π_3,1(R) = [ t | t = <t₃ , t₁> ∧ <t₁ , t₂ , t₃ > ∈ R ]

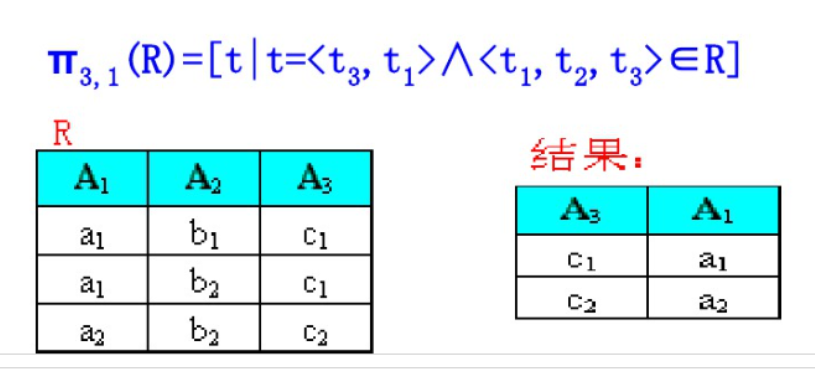
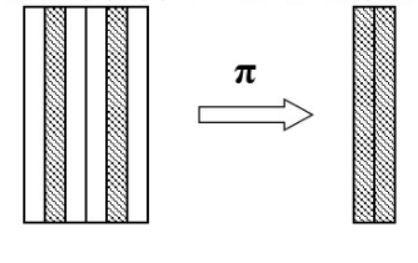
2.2 投影操作主要是从列的角度进行运算

但投影之后不仅取消了原关系中的某些列，而且还可能取消元组(避免重复行)

3. 连接（Join）

连接有三种：θ连接和自然联接（这里是算术比较符），外连接。

一般的连接操作是从行的角度进行运算。不过自然连接还需要取消重复列，所以是同时从行和列的角度进行运算。

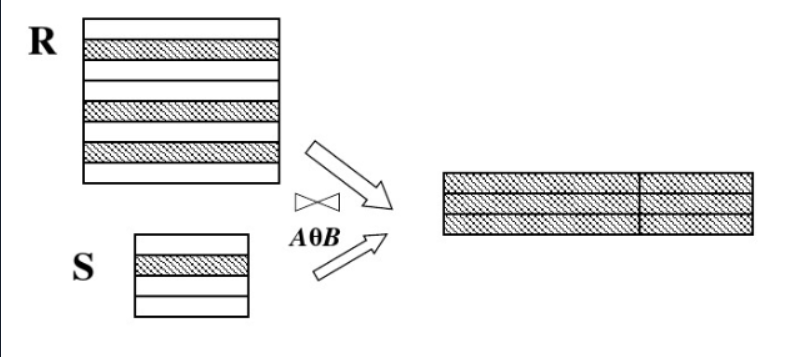
3.1 θ连接

连接也称为θ连接，关系R与关系S的连接运算是从两个关系的笛卡尔积中选取属性间满足一定条件的元组形成一个新的连接。这个条件为θ(比较运算符，如>、<、=)。

3.2 自然连接

是一种特殊的等值连接，比较两个关系中分量相同的属性组，并且在结果中把重复的属性列去掉，最后只保留属性组中分量相同的元组。

3.3 左连接

在自然连接的基础上加上左边表上不包含自然连接中所含元组（行）的元组。

3.4 右连接

在自然连接的基础上加上右边表上不包含自然连接中所含元组（行）的元组。

3.5 外连接

左连接+右连接

4. 除

除法运算的一般形式示意图：

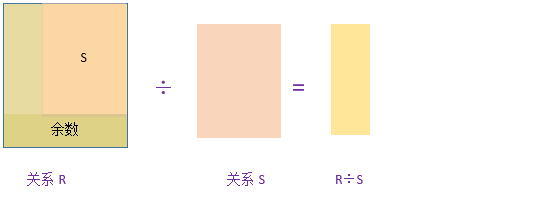
如何计算R÷S呢，首先我们引进”象集”的概念，具体意义看下面的陈述即可理解

关系R和关系S拥有共同的属性B、C
R÷S得到的属性值就是关系R包含而关系S不包含的属性，即A属性

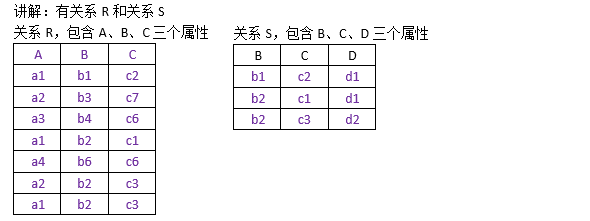
在R关系中A属性的值可以取{ a1，a2，a3，a4 }

a1值对应的象集为 { (b1,c2) , (b2,c1) , (b2,c3) }
a2值对应的象集为 { (b3,c7) , (b2,c3) }
a3值对应的象集为 { (b4,c6) }
a4值对应的象集为 { (b6,c6) }

关系S在B、C上的投影为 {(b1,c2) , (b2,c1) , (b2,c3)}

只有a1值对应的象集包含关系S的投影集，所以只有a1应该包含在A属性中

所以R÷S为:

blog.csdn.net/u012411414/…

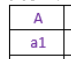
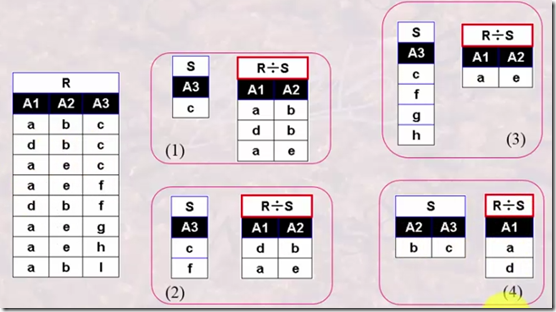
除操作比较复杂，它是一种全包含操作，通过下面的例子来解释除操作

在(1)中计算R除以S操作，首先生成的关系中没有R和S的公共属性A3。其次生成的关系中每个元组与S中的元组进行组合都能出现在R中。

在(3)中只有(a,e)的原因是只有(a,e)与S中的每个元组组合才能出现在R中，而像(d,b)这种元组如果如S中每个元组组合的话不能全部出现在R中。

在(2)中我们可以这样来理解除法运算，找出即出现c又出现f的元组，并且这些元组的其余属性值是相等的。如包含c和f的元组有【(a,b,c)】,【(d,b,c),(d,b,f)】【(a,e,c),(a,e,f)】,其余属性值相等的有(a,e),(d,b)。

关系代数知识点