从0.1+0.2不等于0.3看javascript数据表示

    很多同学可能都遇到过这样一个问题：Boolean(0.1+0.2==0.3)，结果尽然是false，what？这简直再挑战我们的数学常识，那这究竟是为什么呢？

    计算机的数据存储形式-二进制

    要想弄懂我们开头的问题，首先要搞懂一个概念，就是计算机的数据存储机制。大家都知道计算机实际是由集成电路构成的，每条微小的电路都有通断两个状态，因此计算机的信息数据只能用二进制来表示。

    二进制表示整数

      二进制表示数值的原理其实与十进制相同，比如十进制数39，其各个位数的数字并不是简单的3和9。其中3表示3x10=30，9表示9x1=9。其中各个位数的数字乘以的10和1叫位权。位权的思考方式同样适用于二进制。即第一位是2的0次幂(1)，第二位是2的一次幂(2)...。oo的xx次幂表示位权，十进制情况下oo是10，二进制情况下是2，这个称为基数。

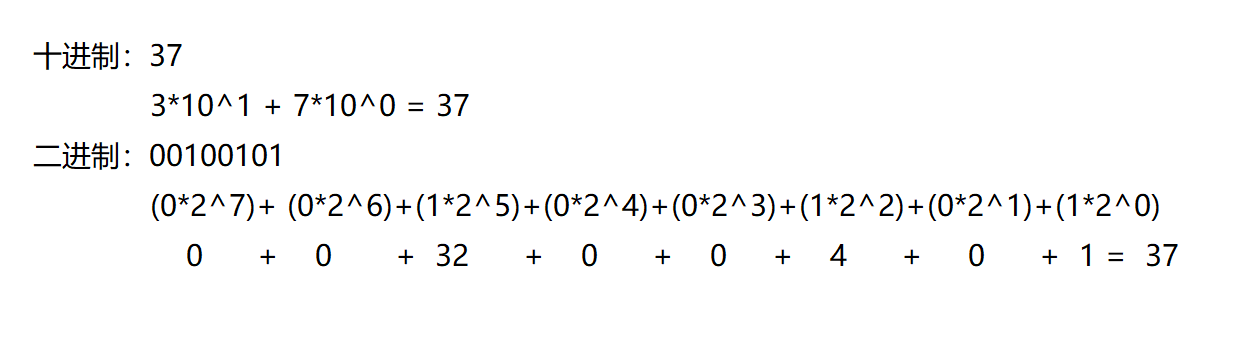
二进制表示小数

    二进制小数的表示也是类比十进制的小数表示。例如十进制小数0.35，我们知道是35除以10再除以10得到的，那么以0.35乘以10再乘以10之后就是35，3和5分别通过乘10取整之后得到。同理二进制小数的方法就是：乘2取整，顺序排列。    

举个“栗子”： 

 将0.35进行二进制表示

 0.35*2=0.7  取整为0

 0.7*2=1.4     取整为1 

 0.4*2=0.8     取整为0

 0.8*2=1.6      取整为1

 0.6*2=1.2      取整为1

 ...直到小数部分为0，显然这里会无限循环下去。 所以一般会取前面的十几位二进制数尽量接近表示0.35。

由于这种计算的规则，从而对于不等于1/2^n（n>=1，n为整数）的小数，二进制是不能精确表示的。

 0.1+0.2的结果

0.1==》0.1.toString(2)==》0.0001100110011(无限循环..)

0.2==》0.2.toString(2)==》0.001100110011(无限循环..)

所以说：0.1 +0.2=0.30000000000000004

解决办法

1.给出明确的精度要求，在返回值的过程中，计算机会自动四舍五入

let num1 = 0.1; 
let num2 = 0.2; 
Booleam( parseFloat((num1 + num2).toFixed(2)) === 0.30 );

2.自己写一个方法专门处理，这个百度有很多，大家自行查找即可。