什么是快速排序的思想呢?
百度百科上的快速排序说明 通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
画重点:
- 通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小;
- 使用相同的方法对这两部分数据分别进行快速排序;
- 整个排序过程可以递归进行,以此达到整个数据变成有序序列;
问题
-
怎么才能区分两个部分的数据呢?
通常取这一趟排序的第一个数字或者最后一个数字作为基准数字
-
怎么排序?
将大于基准数字的放到数组的右边, 小于改数值的数字放在左边, 等于的放在中间(这个不用递归排序了), 然后再次对左边和右边的数列继续做相同的处理, 重复 1 和 2 直到 待排序得数列中只有一个数字或者为空的时候;
-
怎么定义递归的出口呢?
当待排序的数列长度小于等于 1 的时候
实现排序
假设排序的数列是: arr = [2, 0, 2, 0, 0, 6, 0, 8]
- 取第一个数作为基准数字: 2 那么从 arr[1] 开始, arr[1] 为 0, 小于 2, 放在 左边; arr[2] 为 2, 等于 2, 放在中间; arr[3] 等于 0, 小于 2 放在左边; ... ; arr[5] 等于 6, 大于2 放在右边; ...
- 经过 1 之后, 得到三个数列为: lt = [0, 0, 0, 0], eq = [2, 2] 和 gt = [6, 8]
- 然后对 lt 和 gt 使用相同的逻辑 1 进行处理, 直到数列的 lt 和 gt 的长度都小于等于 1
- 最后把 lt, eq, gt 合并输出
type adt int
// 最原始的的快速排序方法
func lazySort(arr []adt) []adt {
// 递归的出口
if len(arr) <= 1 {
return arr
}
// 存放比基准数值小的数列
lt := make([]adt, 0)
// 存放等于基准数的数列
eq := make([]adt, 0)
// 存放比基准数大的数列
gt := make([]adt, 0)
// 取第一个数值为基准数字
eq = append(eq, arr[0])
std := arr[0]
for i := 1; i < len(arr); i++ {
// 如果当前的数字比基准数值小, 把当前的数字放入 lt 数列
if arr[i] < std {
lt = append(lt, arr[i])
continue
}
// 如果当前的数值比基准数大, 把当前的数字放入 gt 数列
if arr[i] > std {
gt = append(gt, arr[i])
continue
}
eq = append(eq, arr[i])
}
// 递归调用 排序, 然后将结果组成一个新的数列返回
return append(lazySort(lt), append(eq, lazySort(gt)...)...)
}
测试:
func main(){
var std = []adt{2, 0, 2, 0, 0, 6, 0, 8}
lazySort(std)
fmt.Println(lazySort(std))
}
嗯: 这个还需要优化, 开辟的空间太多了, 但是这个是从快速排序的思想上粗发的, 最好理解
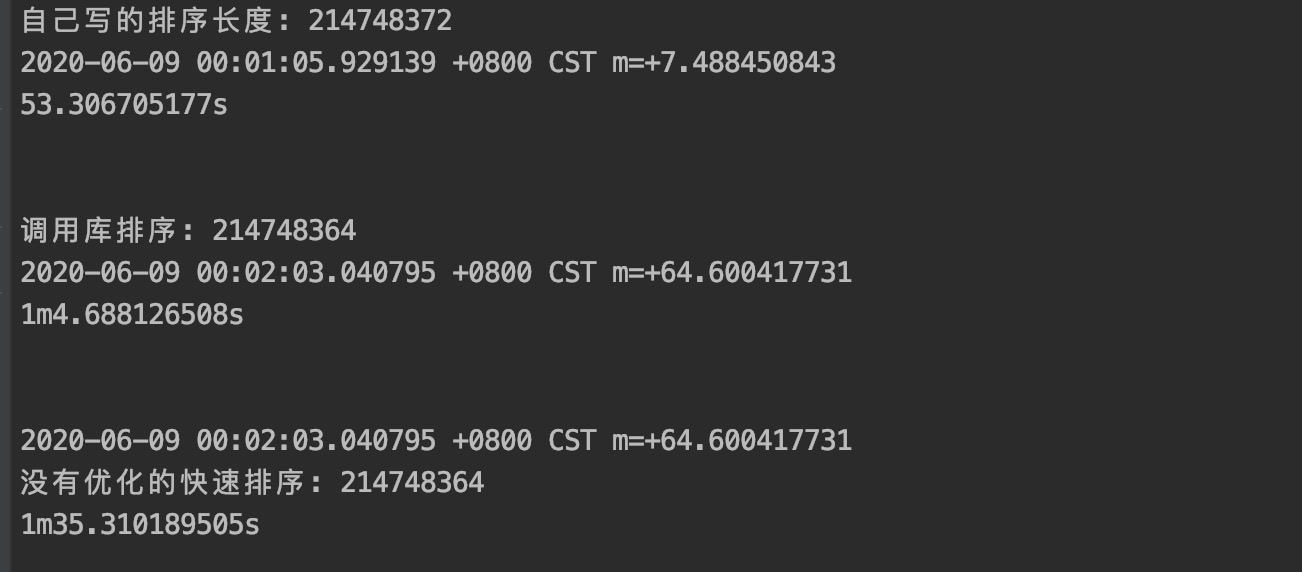
第一个不是使用上面的实现, 使用的是相同的思想加上插入排序完成的
第二个是调用库函数的排序
第三个是纯粹的快速排序的思想