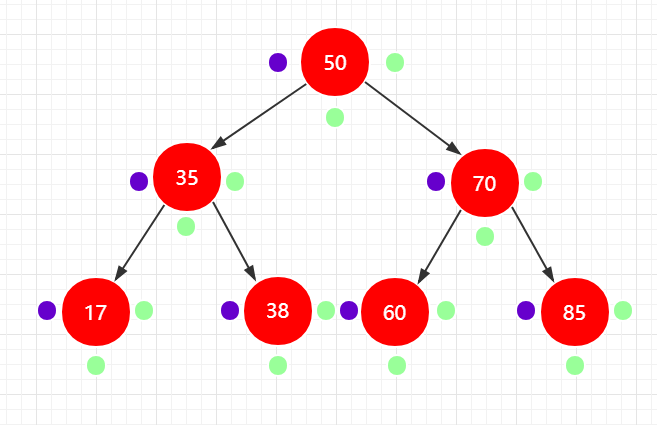
代码实现二分搜索树
package com.example.demo.tree.bintree;
import java.util.LinkedList;
import java.util.Objects;
import java.util.Queue;
import java.util.Stack;
/**
* 二分搜索树
* 左孩子小于父节点
* 猴孩子大于父节点
*
* @param <E>
*/
public class BinTree<E extends Comparable<E>> {
private class Node {
public E e;
public Node left, right;
public Node(E e) {
this.e = e;
left = null;
right = null;
}
}
private Node root;
private int size;
public BinTree() {
root = null;
size = 0;
}
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
// 递归插入元素
@Deprecated
private void add2(Node node, E e) {
if (e.equals(node.e)) {
return;
} else if (e.compareTo(node.e) < 0 && node.left == null) {
node.left = new Node(e);
size++;
return;
} else if (e.compareTo(node.e) > 0 && node.right == null) {
node.right = new Node(e);
size++;
return;
}
// 当根节点孩子节点不为空时,以孩子节点为根递归插入
if (e.compareTo(node.e) < 0) {
add2(node.left, e);
} else {
add2(node.right, e);
}
}
/**
* 向二分搜索树中添加新元素e
*
* @param e
*/
public void add(E e) {
root = add(root, e);
}
/**
* 返回插入新节点后二分搜索树的根
*
* @param node
* @param e
* @return
*/
private Node add(Node node, E e) {
// 如果node为空则初始化一个新的根节点
if (node == null) {
size++;
return new Node(e);
}
// 当根节点孩子节点不为空时,以孩子节点为根递归插入
if (e.compareTo(node.e) < 0) {
node.left = add(node.left, e);
} else if (e.compareTo(node.e) > 0) {
node.right = add(node.right, e);
}
return node;
}
/**
* 查询二分搜索树是否包含e
*
* @param e
* @return
*/
public boolean contains(E e) {
return contains(root, e);
}
/**
* 查询以node为根的二分搜索树是否包含e
*
* @param node
* @param e
* @return
*/
private boolean contains(Node node, E e) {
if (node == null) {
return false;
}
if (e.compareTo(node.e) == 0) {
return true;
} else if (e.compareTo(node.e) < 0) {
return contains(node.left, e);
} else {
return contains(node.right, e);
}
}
/**
* 前序遍历(遍历方式体现的访问节点的先后)
* <p>
* 该节点
* traverse(node.left)
* traverse(node.right)
* ===============================================
* <p>
* 中序遍历, 中序遍历的结果就是数据排序后的结果
* <p>
* traverse(node.left)
* 该节点
* traverse(node.right)
* ===============================================
* <p>
* 后序遍历
* <p>
* traverse(node.left)
* traverse(node.right)
* 该节点
*/
public void preOrder() {
preOrder(root);
}
public void inOrder() {
inOrder(root);
}
public void postOrder() {
postOrder(root);
}
/**
* 前序遍历
*
* @param node
*/
private void preOrder(Node node) {
if (Objects.isNull(node)) {
return;
}
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
/**
* 中序遍历
*
* @param node
*/
private void inOrder(Node node) {
if (Objects.isNull(node)) {
return;
}
inOrder(node.left);
System.out.println(node.e);
inOrder(node.right);
}
/**
* 后序遍历
* 应用:内存释放方面
*
* @param node
*/
private void postOrder(Node node) {
if (Objects.isNull(node)) {
return;
}
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
}
/**
* 非递归前序遍历(一种写法没什么卵用,还是用递归比较好)
* 利用栈后进先出的原理
*/
public void preOrderNR() {
Stack<Node> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
Node cur = stack.pop();
System.out.println(cur.e);
if (cur.right != null) {
stack.push(cur.right);
}
if (cur.left != null) {
stack.push(cur.left);
}
}
}
/**
* 使用队列实现层序遍历
* 广度优先
*/
public void levelOrder() {
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
Node cur = queue.remove();
System.out.println(cur.e);
if (Objects.nonNull(cur.left)) {
queue.add(cur.left);
}
if (Objects.nonNull(cur.right)) {
queue.add(cur.right);
}
}
}
public E minNode() {
if (size == 0) {
throw new IllegalArgumentException("Bin Tree is empty");
}
Node minNode = minNode(root);
return minNode.e;
}
/**
* 寻找二分查找树中的最小元素
*
* @param node
* @return
*/
private Node minNode(Node node) {
if (Objects.isNull(node.left)) {
return node;
}
return minNode(node.left);
}
public E maxNode() {
if (size == 0) {
throw new IllegalArgumentException("Bin Tree is empty");
}
Node node = maxNode(root);
return node.e;
}
/**
* 寻找二分查找树中的最大元素
*
* @param node
* @return
*/
private Node maxNode(Node node) {
if (Objects.isNull(node.left)) {
return node;
}
return maxNode(node.right);
}
public E removeMin() {
E ret = minNode();
root = removeMin(root);
return ret;
}
/**
* 删除以node为根的二分搜索树中最小的节点
*
* @param node
* @return
*/
private Node removeMin(Node node) {
if (Objects.isNull(node.left)) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
public E removeMax() {
E ret = maxNode();
root = removeMax(root);
return ret;
}
/**
* 删除以node为根的二分搜索树中的最大节点
*
* @param node
* @return
*/
private Node removeMax(Node node) {
if (Objects.isNull(node.right)) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
public static void main(String[] args) {
BinTree<Integer> bst = new BinTree<>();
int[] nums = {5, 6, 8, 9, 7, 2, 3, 85};
for (int num : nums) {
bst.add(num);
}
bst.preOrderNR();
System.out.println("================================");
bst.preOrder();
System.out.println("================================");
bst.inOrder();
System.out.println("================================");
bst.postOrder();
}
}
