复杂度
O的概念用来描述算法的复杂度,简而言之就是算法执行所需要的执行次数和数据量的关系(时间复杂度);占用额外空间和数据量的关系(空间复杂度)
常见的复杂度:
* O(1): 常量复杂度(和数据量没有关系),从数组中取出第i个元素:arr[i]
* 0(log n): 对数复杂度(每次二分)
* 0(n): 线性时间复杂度(数组遍历一次)
* 0(n*log n): 线性对数(遍历+二分)
* 0(n^2):平方方两层遍历(从这里开始,意味着后面的算法基本不可用)
* 0(n^3):立方
* 0(2^n):指数
* 0(n!):阶乘
基本排序算法
冒泡排序:O(n^2)
最经典和简单粗暴的排序算法,简而言之就是挨个对比,如果相邻右边的数大就交换位置,遍历一遍,最大的在最右边,重复步骤,完成排序;
const arr = [10,1,35,61,89,36,55];
function bubbleSort(arr) {
var len = arr.length;
for (let outer = len ; outer >= 2; outer--) {
for(let inner = 0; inner <=outer - 1; inner++) {
if(arr[inner] > arr[inner + 1]) {
let temp = arr[inner];
arr[inner] = arr[inner + 1];
arr[inner + 1] = temp;
}
}
}
return arr;
}
console.log(bubbleSort(arr));
面试官可能会问有更简单的方式吗?没有问自己说,装c 那就是ES6中数组的解构赋值
function bubleSort(arr) {
var len = arr.length;
for (let outer = len; outer >= 2; outer--) {
for (let inner = 0; inner <= outer - 1; inner++) {
if (arr[inner] > arr[inner + 1]) {
[arr[inner], arr[inner + 1]] = [arr[inner + 1], arr[inner]];
}
}
}
return arr;
}
console.log('bubleSort', bubleSort([3, 5, 1, 2, 7, 2, 1]));
选择排序
选择排序是从数组的开头开始,将第一个元素和其他元素进行比较。检查完所有元素后,最小的元素会被放到数组的第一个位置,然后算法会从第二个位置继续。这个过程循环进行,当进行到数组的倒数第二个位置时,便完成了排序。
插入排序
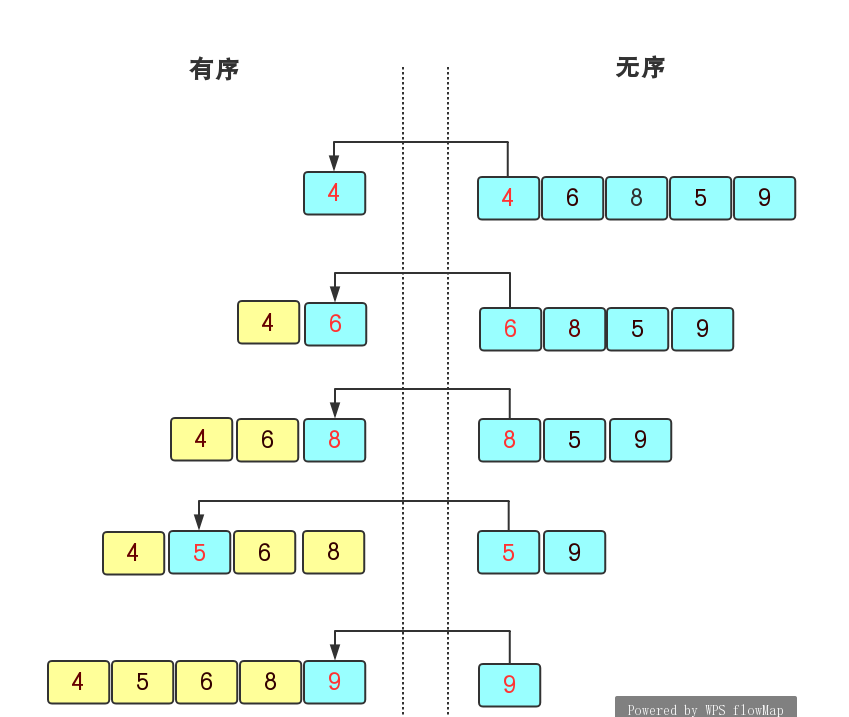
插入排序是将无序序列中的数据插入到有序的序列中,在遍历无序序列时,首先拿无序序列中的首元素去与有序序列中的每一个元素比较并插入到合适的位置,一直到无序序列中的所有元素插完为止。对于一个无序序列arr{4,6,8,5,9}来说,我们首先先确定首元素4是有序的,然后在无序序列中向右遍历,6大于4则它插入到4的后面,再继续遍历到8,8大于6则插入到6的后面,这样继续直到得到有序序列{4,5,6,8,9}
function insertSort (arr) {
/**
* 走一波代码执行流程:
* i = 1 1<9
* j=i=1 1>0
* 5 < 3 ? false break
* j-- j=0 0>0? false 第一次的内循环结束
* i++ i=2 2<9
* j=i=2 2>0
* arr[2]=8 < arr[1]=5 false break
* j-- j=1 1>0? true
* arr[1]=5 < arr[0]=3 ? false 第二次的内循环结束
* i++ i=3 3<9
* j=i=3 3>0
* arr[3]=2 < arr[2]=8 true 交换位置 arr[3]=8 arr[2]=2
* j-- j=2>0
* arr[2]=2 < arr[1]=5 true 交换位置 arr[1]=2 arr[2]=5
* j-- j=1>0
* arr[1] < arr[0]=3 true 交换位置 arr[0]=2 arr[1]=3
* [2, 3, 5, 8, 9, 13, 33, 1, 55]
*
*/
for (let i = 1; i < arr.length; i++) {
for (let j = i; j > 0; j--) {
if (arr[j] < arr[j - 1]){
[arr[j], arr[j - 1]] = [arr[j - 1], arr[j]];
} else {
break;
}
}
}
}
const data = [3, 5, 8, 2, 9, 13, 33, 1, 55];
insertSort(data);
console.log(data);
高级一点的排序算法
通常被认为是处理大型数据集的最高效排序算法
希尔排序
插入排序的改进版的非稳定算法,核心理念与插入不同,它会首先比较距离较远的,而非相邻的元素。这样可以使离正确位置很远的元素更快回到合适的位置。
快速排序: 复杂度(线性对数) O(nlogn)
快速排序重点在于对数组的拆分,通常将数组的第一个元素定义为比较元素,然后将数组中小于比较元素的数放左边,将大于比较元素的数放在右边;这样就将数组拆分成了左右两部分: 小于比较元素的部分 比较元素 大于比较元素的部分; 然后再将左右两部分进行同样的拆分,直到不能继续拆分,数组自然而然就排好序了;
// 快速排序:这个版本会额外占用空间,并不是最优的,但是好理解
const arr = [4, 9, 3, 5, 2, 6, 8, 1];
function quickSort(arr) {
if (arr.length <= 1) {
return arr;
}
// 1.找一个标志位
const flag = arr.shift();
// 2.遍历数组,将小于标志位的元素放左边,大于标志位的元素放右边
const left = [];
const right = [];
// 3. 对左右两边递归调用quickSort
// 4. 终止条件
for (let i = 0; i < arr.length; i++) {
const item = arr[i];
if (item < flag){
// 放左边
left.push(item);
} else {
// 放右边
right.push(item);
}
}
return quickSort(left).concat(flag, quickSort(right));
}
console.log('排序后的结果', quickSort(arr)); // [1, 2, 3, 4, 5, 6, 8, 9]
原地快排:不占用额外空间,原地交换数据完成,两个指针,分别一个在排头一个在排尾
// 原地快排
const arr = [7, 5, 8, 6];
function quickSort(arr, low = 0, high = arr.length-1) {
if ( low >= high ) {
return;
}
let left = low;
let right = high;
let flag = arr[left];
while (left < right) {
// 右边开始比找到比flag小的数
if (left < right && flag <= arr[right]) {
right--;
}
arr[left] = arr[right];
// 左边开始找
if(left < right && flag >= arr[left]) {
left++;
}
arr[right] = arr[left];
}
arr[left] = flag;
// 对arr[left] 左边使用递归
quickSort(arr, low, left - 1);
// 对arr[left] 右边使用递归
quickSort(arr, left + 1, right);
}
quickSort(arr);
console.log(arr);
递归
在快排中使用到了递归,递归就是自己调用自己,形成一个调用栈,逐渐缩小目标,达到截至条件返回指向的逻辑;从顶向下,问题分解
常见的案例:数组扁平化 数据深克隆
const arr = [1, 2, [4, 5, [6, 7, [8]]]];
Array.prototype.flat = function() {
let res = [];
this.forEach((item) => {
if (Array.isArray(item)) {
// 递归
res = res.concat(item.flat());
} else {
res.push(item)
}
});
return res;
}
const oneDimensional = arr.flat();
console.log(oneDimensional);
爬梯问题(递归到动态规划的演进)
有一楼梯,刚开始时你再第一级,若每次只能垮一个阶梯或两个阶梯,要走上第10级,共有多少种走法?
其实就是一个斐波那契数列,只有两种方式, 从第9层上一级,或者从第8层上两级
所在层数 走的方式 方式总计
1 1 1
2 2, 1 2
3 1 1 1,1 2, 2 1 3
4 1 1 1 1, 2 2,2 1 1,1 1 2, 1 2 1 5
5 ...... 8
6 ..... 13
7 ...... 21
8 ..... 34
9 ...... 55
10 ...... 89
暴力递归,时间复杂度O(2^n)
function stairs(n) {
if (n === 0 || n === 2) {
return 1;
} else if (n < 0) {
return 0;
} else {
return stairs(n - 1) + stairs(n - 2);
}
}
console.time('stairs');
console.log(stairs(40)); // 耗时: 1151.682ms
console.timeEnd('stairs');
有备忘录的递归,给每次计算的结果做一个缓存,基本上是时间复杂度是O(n),与暴力的相比,是降维打击;
// 做了缓存优化的爬梯问题
function fib (n) {
const cache = [];
return helper(cache, n);
}
function helper(cache, n) {
if (n === 1 || n === 2) {
return 1
}
if (cache[n]) {
return cache[n];
}
cache[n] = helper(cache, n - 1) + helper(cache, n - 2);
return cache[n]
}
console.time('fib');
console.log(fib(40)); // 计算耗时: 3.890ms
console.timeEnd('fib');
基本递归,都可以用循环替代
function fibBest(n) {
const dp = [];
dp[1] = dp[2] = 1;
for (let i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}