机器学习-线性代数-线性代数中表示空间的最简洁的形式在一维空间,我们可以直观化为一个数轴. 自由度指的就是我们可以到达数

1.简介

数学追求的是理论完美,表示方法最简单.这里仅仅塔伦可以看到的一维,二维和三维空间,我们可以借助几何方法将其直观化. 数学中的空间指的就是自由度.

2.一维空间

在一维空间,我们可以直观化为一个数轴. 自由度指的就是我们可以到达数轴的任意位置. 假设我们现在就站在数轴上, 每秒可以走一米(1m/s), 我们可以走到数轴的任意位置, 唯一需要关注的是走到某个位置需要花费多少时间.

3. 二维空间

3.1 矩阵为2行2列的情况

二维空间稍微复杂一点.因为有两个移动方向, 左右和上下.

在二维空间, 我们可以采用一步一动的方式来实现向量的操作

假设我们在二维坐标系中移动单位距离,每秒可以走一米(1m/s),首先定义两个方向, 左右方向定义为 $\begin{bmatrix} 1\\ 0 \end{bmatrix}$ , 上下方向定义为 $\begin{bmatrix} 0\\ 1 \end{bmatrix}$

合并的一个矩阵中,这个矩阵有两列, 第一列告诉我们在左右方向的移动速度, 第二列告诉我们上下方向的移动速度

\begin{bmatrix}
1 &0 \\
0& 1
\end{bmatrix}

这个矩阵就是表示二维空间的单位矩阵, 通过组合这两列,我们可以到达二维空间中的任意位置.使用矩阵乘法, 组合矩阵的两列.

\begin{bmatrix}
1 &0 \\
0& 1
\end{bmatrix}*\begin{bmatrix}
x\\ y\end{bmatrix}=x\begin{bmatrix}
1\\
0
\end{bmatrix}+y\begin{bmatrix}
0\\
1
\end{bmatrix}

$\begin{bmatrix} x\\ y \end{bmatrix}$ 向量告诉了我们如何在坐标系的两个方向上移动, $x$ 指定了左右方向的移动, $y$ 指定了上下方向的移动. 例如向量 $\begin{bmatrix} 1\\ 1 \end{bmatrix}$ 通知矩阵在左右方向移动一个单位, 上下方向移动一个单位,最后我们移动到 $\begin{bmatrix} 1\\ 1 \end{bmatrix}$ 这个位置 .

\begin{bmatrix}
1 &0 \\
0& 1
\end{bmatrix}*\begin{bmatrix}
1\\ 1\end{bmatrix}=1\begin{bmatrix}
1\\
0
\end{bmatrix}+1\begin{bmatrix}
0\\
1
\end{bmatrix}=\begin{bmatrix}
1\\
1
\end{bmatrix}

对于学习者比较迷惑的是 $\begin{bmatrix} 1\\ 1 \end{bmatrix}$ , 在矩阵组合里的 $\begin{bmatrix} 1\\ 1 \end{bmatrix}$ 是描述矩阵列的组合方式, 结果里的 $\begin{bmatrix} 1\\ 1 \end{bmatrix}$ 是描述生成了一个什么向量. 第一个可以成为定义域, 第二个可以成为值域, 虽然在这里两个向量是写出来是一样的但是意义是不同的. 第一个 $\begin{bmatrix} 1\\ 1 \end{bmatrix}$ 是属于 $R^{n}$ 空间, 描述了矩阵中n列向量的组合情况. 结果是属于 $R^{m}$ 空间, 描述了生成的向量的维度. 之所以会 $\begin{bmatrix} 1\\ 1 \end{bmatrix}$ ,相同是因为矩阵的结构是 $2*2$ 的形式. 我们在看看 $2*3$ 的情况.

3.2 矩阵为2行3列( $2*3$ )的情况

在二维空间中,我们仅仅只需要在两个方向移动不同的距离就可以到达空间中所有的位置,在一般情况下就可以满足向量组合的需求,但是也有特殊情况,比如下面的矩阵:

\begin{bmatrix}
1 & 0& 3\\
0 & 1 & 0
\end{bmatrix}

在坐标系中画出三个向量, 会发现第一列的向量和第三列的向量方向是相同的, 这两列的组合只能让生成的向量在左右方向上移动,由于这两个向量可以有很多组合达成和一个向量移动相同的效果, 因此让解集变得很多样化.

\begin{bmatrix}
1 & 0& 3\\
0 & 1 & 0\end{bmatrix}*\begin{bmatrix}
x\\ y
\\ z\end{bmatrix}=x\begin{bmatrix}
1\\
0
\end{bmatrix}+y\begin{bmatrix}
0\\
1
\end{bmatrix}+z\begin{bmatrix}
3\\
0
\end{bmatrix}

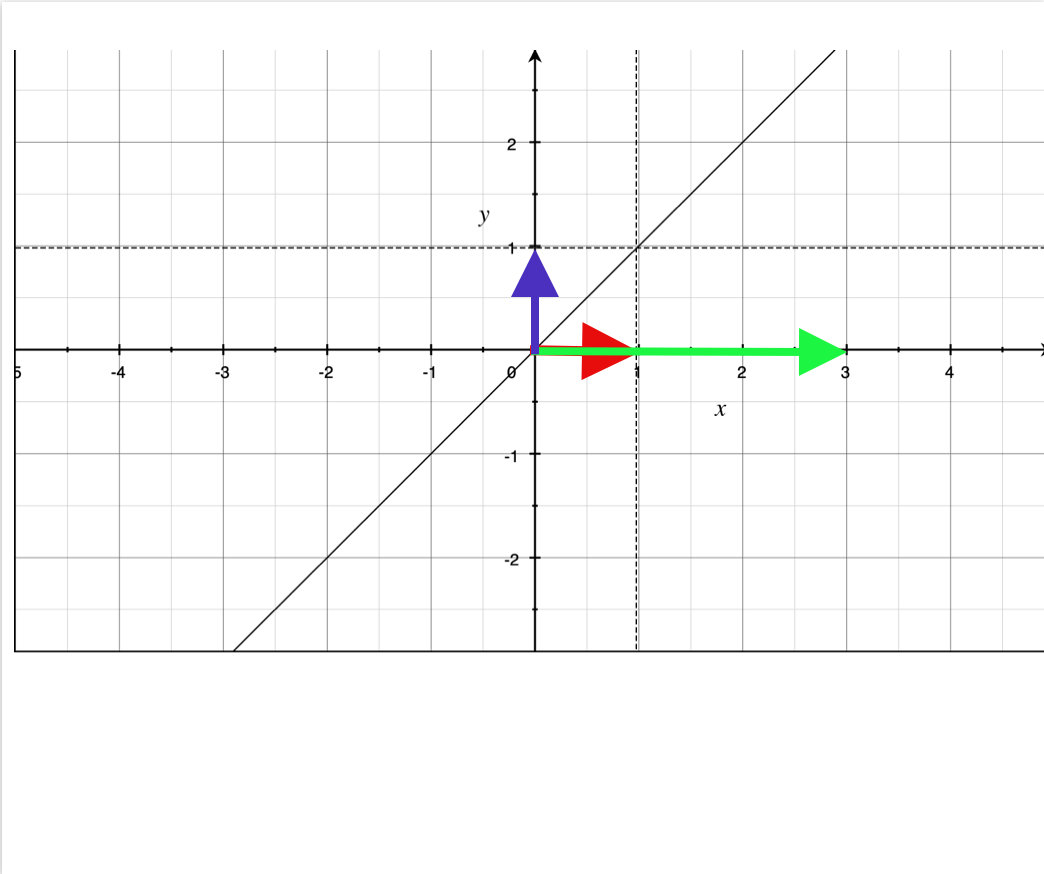
如果我们想向右走5米, 第一列向量可以乘以系数2, 第三列向量可以乘以系数3,或者第一列向量乘以系数5,第三列向量乘以0, 这里可以有很多的组合方式.也就是说在矩阵中如果有向量方向相同, 产生的组合就比较多了, 可以获得无限种组合方式.

3.3 矩阵为2行3列( $2*3$ )的一般情况

如果我们把第三列向量在改变一下

\begin{bmatrix}
1 & 0& 1\\
0 & 1 & 1
\end{bmatrix}

第三列的方向似乎和第一列,第二列的方向都不同但是如果回顾前面的计算结果:

我们就可以知道第三列实际就是第一列和第二列经过组合后的结果, 可以逆向把它分解开

\begin{bmatrix}
1 &0 &1 &0 \\
0&1 &0 &1
\end{bmatrix}

这样处理以后在矩阵中就只有两个方向了.第三列的向量组合了左右和上下两个方向这个地方值得好好的思考一下.

4. 三维空间的情况

线性代数随着维度的增加,思考起来难度增加了, 在三维空间之内,我们可以借助几何直观来研究问题,熟悉问题, 所以学习的时候最好在三维空间的情况下反复的练习, 在自然过渡到高位空间时处理方法是一样的. 上面我们研究了一维和二维空间下的情况, 现在看看三维空间情况, 为了说明问题,我们还是采取一步一动的方式

定义一个三维空间的单位矩阵:

\begin{bmatrix}
1 &0 &0 \\
0& 1 &0 \\
0& 0 & 1
\end{bmatrix}

在三维坐标系中先画出这三个向量, 其实就是三维直角坐标系的三个轴的方向,可以想象这个坐标系放在墙角

想象你是一只苍蝇, 从这个角落可以飞到屋子里的任何地方, 任何地方的意思是可以左右飞,可以前后飞, 可以上下飞. 上面的矩阵就描述了三个方向, 所以可以我们可以定量化描述苍蝇飞到了空间的那一个位置,仍然采用一步一动的方式处理.

\begin{bmatrix}
1 &0 &0 \\
0& 1 &0 \\
0& 0 & 1\end{bmatrix}\begin{bmatrix}
1\\ 1
\\ 1\end{bmatrix}=1*\begin{bmatrix}
1\\ 0
\\ 0\end{bmatrix}+1*\begin{bmatrix}
0\\ 1
\\ 0\end{bmatrix}+1*\begin{bmatrix}
0\\ 0
\\ 1\end{bmatrix}=\begin{bmatrix}
1\\ 1
\\ 1\end{bmatrix}

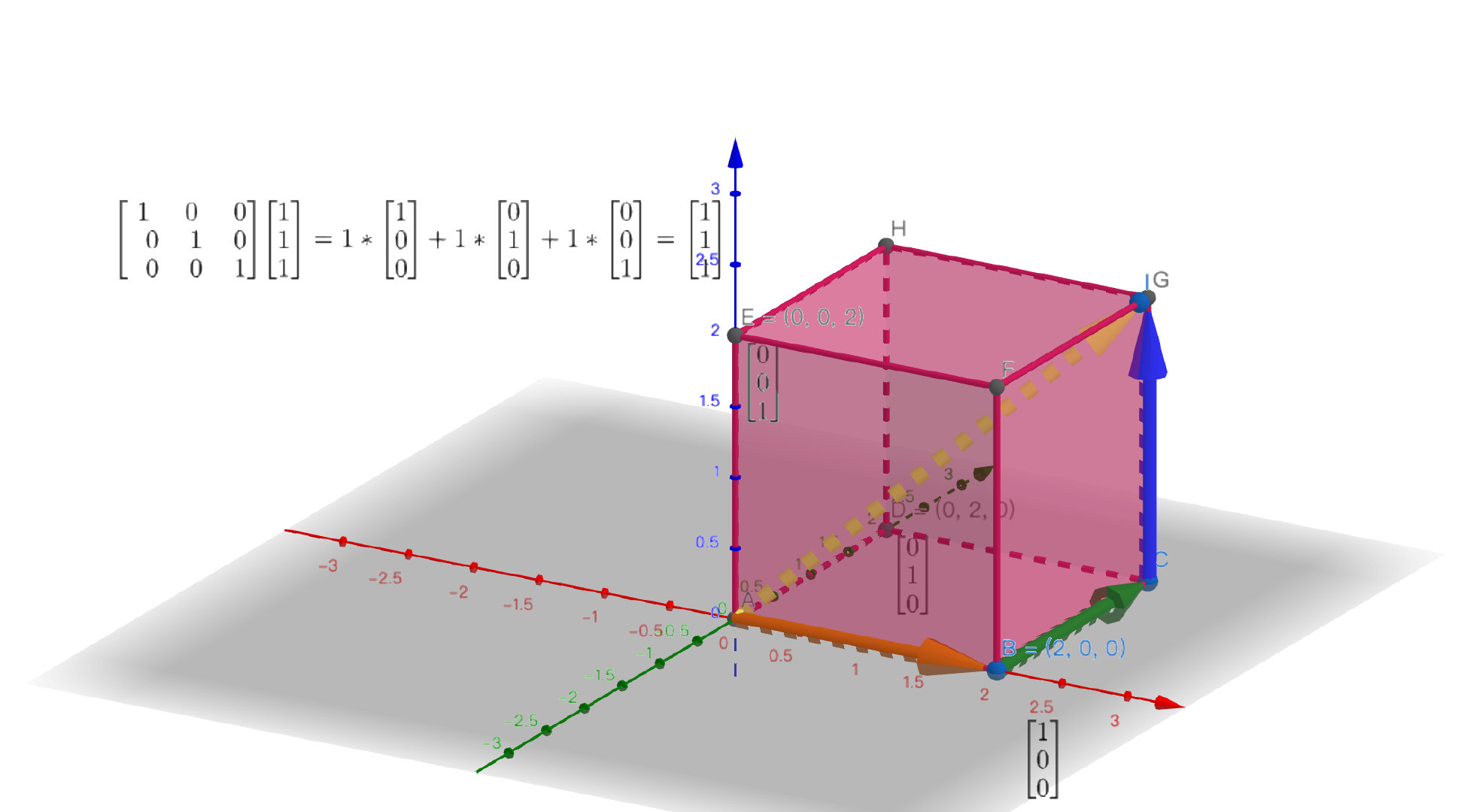
一步一动执行矩阵和向量的乘法, 第一步沿着 $\begin{bmatrix} 1\\ 0 \\ 0\end{bmatrix}$ (红色坐标轴方向)方向移动一个单位, 第二步沿着 $\begin{bmatrix} 0\\ 1 \\ 0\end{bmatrix}$ (绿色坐标轴的平行方向)方向移动一个单位, 第三步沿着 $\begin{bmatrix} 0\\ 0 \\ 1\end{bmatrix}$ (蓝色坐标轴平行方向)方向移动一个单位, 最终的向量就是 $\begin{bmatrix} 1\\ 1 \\ 1\end{bmatrix}$ , 在图中就是正方体的对角线方向.

4.1 向量稍微改变一下怎么处理

下面我们看怎么得到 $\begin{bmatrix} 1\\ 2 \\ 3\end{bmatrix}$ 这个向量,现在不用画出来,还是一步一动, 第一步沿着 $\begin{bmatrix} 1\\ 0 \\ 0\end{bmatrix}$ 方向移动一个单位, 第二步沿着 $\begin{bmatrix} 0\\ 1 \\ 0\end{bmatrix}$ 方向移动2个单位, 第三步沿着 $\begin{bmatrix} 0\\ 0 \\ 1\end{bmatrix}$ 方向移动3个单位, 最终的向量就是 $\begin{bmatrix} 1\\ 2 \\ 3\end{bmatrix}$

\begin{bmatrix}
1 &0 &0 \\
0& 1 &0 \\
0& 0 & 1\end{bmatrix}\begin{bmatrix}
1\\ 2
\\ 3\end{bmatrix}=1*\begin{bmatrix}
1\\ 0
\\ 0\end{bmatrix}+2*\begin{bmatrix}
0\\ 1
\\ 0\end{bmatrix}+3*\begin{bmatrix}
0\\ 0
\\ 1\end{bmatrix}=\begin{bmatrix}
1\\ 2
\\ 3\end{bmatrix}

反过来,我么也可以这么理解, 在三维空间中,向量 $\begin{bmatrix}1\\2\\3\end{bmatrix}$ 可以分解为三个垂直坐标轴上向量的组合形式,即 $\begin{bmatrix}1\\0\\0\end{bmatrix}$ , $\begin{bmatrix}0\\1\\0\end{bmatrix}$ , $\begin{bmatrix}0\\0\\1\end{bmatrix}$ 三个向量的组合形式.

4.2 如果有一列向量的分量全部为0怎么处理?

比如下面矩阵的第三列:

\begin{bmatrix}
1 &0 &0 \\
0& 1 &0 \\
0& 0 & 0\end{bmatrix}

几何上解释就是一个高度为0,只有长,宽的正方体,也就是一个正方形. 你可以想象一只苍蝇被夹在了两个窗玻璃之间, 它可以在两个方向自由活动,但是飞不出去了.

在线性代数中执行最简消元法,就是要达到这个效果,把没有实际作用的向量消除掉,剩下的是可以组合成新向量的成分.

5. 四维以上的空间

四维以上的空间我们就就画不出来了,但是计算方法和三维是一样的

例如下面这个向量:

\begin{bmatrix}
1 & 0 &0 &0 \\
0&1 &0 &0 \\
0& 0 &1 &0 \\
0 & 0 &0 & 1
\end{bmatrix}

在每个方向都移动一个单位,指令是 $\begin{bmatrix} 1\\ 1\\ 1\\ 1\end{bmatrix}$
写成向量组合形式:

\begin{bmatrix}
1 & 0 &0 &0 \\
0&1 &0 &0 \\
0& 0 &1 &0 \\
0 & 0 &0 & 1
\end{bmatrix}*\begin{bmatrix}
1\\ 1\\ 1\\ 1\end{bmatrix}=1*\begin{bmatrix}
1\\ 0\\ 0\\ 0\end{bmatrix}+1*\begin{bmatrix}
0\\ 1\\ 0\\ 0\end{bmatrix}+1*\begin{bmatrix}
0\\ 0\\ 1\\ 0\end{bmatrix}+1*\begin{bmatrix}
0\\ 0\\ 0\\ 1\end{bmatrix}=\begin{bmatrix}
1\\ 1\\ 1\\ 1\end{bmatrix}

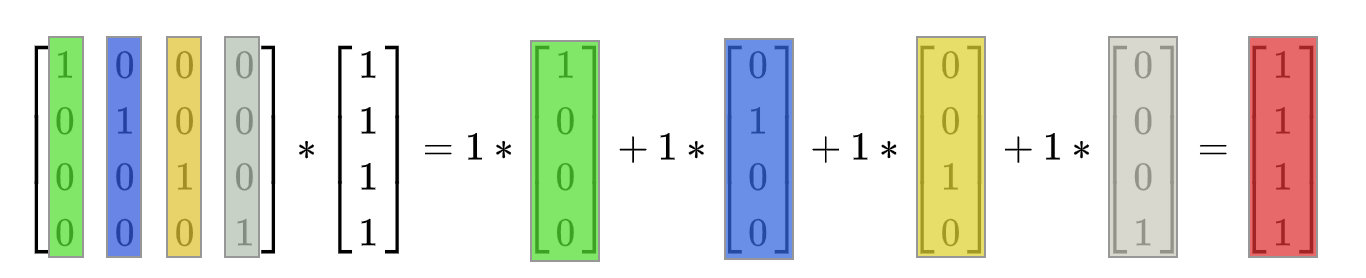
遵循三维空间中一步一动的规则, 在四个方向上分别移动一个单位, 得到的向量就是 $\begin{bmatrix} 1\\ 1\\ 1\\ 1\end{bmatrix}$

6. 结论

以上大致就是线性代数中向量的最简单形式,仔细研究以上的几个问题,就能掌握线性代数的本质问题, 所有的计算都是类似的,对于比较复杂的问题,都可以采用一步一动的分解方式来处理. 之后可以反复练习三维空间中的矩阵形式, 这样在问题不清楚的情况下,可以借助几何方法来简化理解. 矩阵-向量的乘法核心就是矩阵中各列的线性组合, 向量中的每个元素告诉了矩阵在每一列的方向上移动多少距离. 组合生成的向量维度的上限是由矩阵中向量的维度决定的,就是 $m*n$ 中的 $m$ .

机器学习-线性代数-线性代数中表示空间的最简洁的形式