JS 斐波那契数列（Fibonacci）的多种解法leetcode：面试题10- I. 斐波那契数列写一个函数，输入

题

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下：

F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：1

示例 2：

输入：n = 5
输出：5

提示：

0 <= n <= 100

解 1：递归

思路：斐波那契数列的规则就是第三个数是前两个数之和，f(n) = f(n - 1) + f(n - 2)。
用递归写起来很傻，会进行很多无谓的重复运算，运行时间超长，就不展示了。

解 2：迭代存放数组

思路：利用第三个数是前两个数之和的规律，用一个数组 arr 存放在一个循环中从 0 开始的斐波那契数列。

var fib = function(n) {
  if (n < 2) return n

  let arr = [0, 1]

  for (let i = 2; i <= n; i++) {
    arr[i] = (arr[i-1] + arr[i-2]) % 1000000007
  }

  return arr[arr.length-1]
};

时间复杂度：O(n)
空间复杂度：O(n)

解 3：迭代移动

思路：利用第三个数是前两个数之和的规律，用两个变量 a1 a2 在循环中一点一点的向右移动。

var fib = function(n) {
  if (n < 2) return n

  let a1 = 0
  let a2 = 1
  let tmp = 0

  for (let i = 2; i <= n; i++) {
    tmp = a2
    a2 = (a1 + a2) % 1000000007
    a1 = tmp
  }

  return a2
};

时间复杂度：O(n)
空间复杂度：O(1)

解 4：数学通项公式

思路：从数学角度出发，直接用斐波那契数列的通向公式：

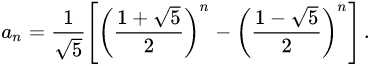
var fib = function(n) {
  if (n < 2) return n

  const sqrt5 = Math.sqrt(5)
  return ((Math.pow((1 + sqrt5) / 2, n) - Math.pow((1 - sqrt5) / 2, n)) / sqrt5) % 1000000007
};

时间复杂度：O(logn)
空间复杂度：O(1)