给我十分钟，搞定二叉树的遍历！

二叉树定义

二叉树是一种树形结构（感觉是废话），它有如下特点：

• 每个节点最多只有两棵子树，即不存在度大于2的节点（度就是树结点的直接子结点数）
• 二叉树的子树有左右之分，其次序不能任意颠倒

二叉树有什么用？

那用处可就大了，就拿我们前端熟悉的来说，抽象语法树（BST）听过吧，babel在编译的时候构建的BST就是一棵二叉树，vue里面的diff，虚拟dom听过吧,这些都离不开二叉树。二叉树的威力远不止如此，利用二叉树前序遍历显示目录结构，利用二叉树中序遍历实现表达式树，在编译器里十分有用，利用二叉树后续遍历实现计算目录内的文件以及信息等。总而言之，二叉树对计算机领域而言可以说是无处不在，熟练运用二叉树，提升程序运行效率，提高程序可读性，优点那么多，赶紧学起来啊

二叉树遍历方式

总的来说，我们可以把遍历二叉树的方式分为4种

• 前序遍历：父结点 -> 左子树 -> 右子树
• 中序遍历：左子树 -> 父结点 -> 右子树
• 后序遍历: 左子树 -> 右子树 -> 父结点
• 层次遍历：逐层访问当前层所有结点，从上到下，从左到右

栗子，如图

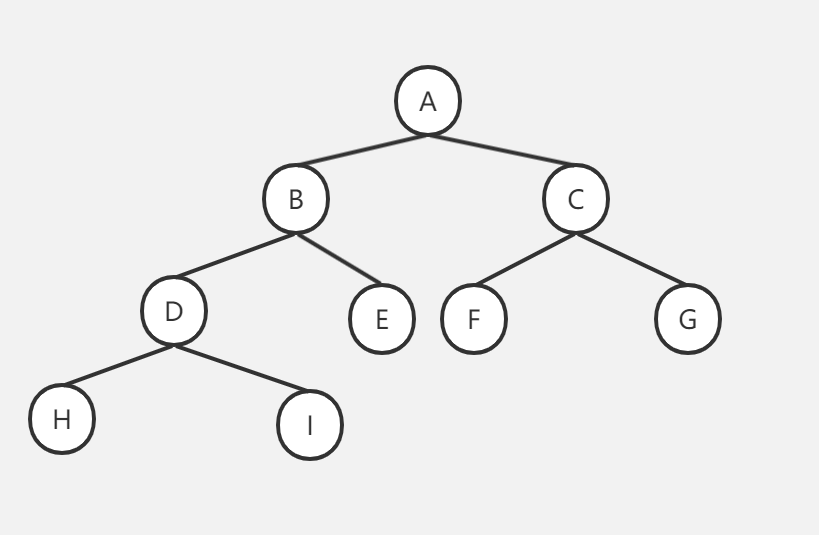
前序遍历结果：ABDHIECFG

中序遍历结果: HDIBEAFCG

后序遍历结果: HIDEBFGCA

层次遍历： ABCDEFGHI

JS二叉树的表达

「结点」

function TreeNode(val) {
     this.val = val;
     this.left = this.right = null;
}

「把上图转化为js里的树：」

var tree = {
    val: "A",
    left: {
        val: "B",
        left: {
            val: "D",
            left: {
                val: "H",
                left: null,
                right: null
            },
            right: {
                val: "I",
                left: null,
                right: null
            }
        },
        right: {
            val: "E",
            left: null,
            right: null
        }
    },
    right: {
        val: "C",
        left: {
            val: "F",
            left: null,
            right: null
        },
        right: {
            val: "G",
            left: null,
            right: null
        }
    }
}

遍历算法

一般来说，树的遍历的方法有递归遍历跟非递归遍历之分，递归遍历优点是代码简单，易于理解，但缺点是执行效率不高。而非递归遍历恰恰是相反，效率高，但代码量大，不易理解。下面先介绍前中后三种的递归遍历方法，其实也可以当作模板去用，很多关于二叉树的问题的本质还是在于遍历上。

递归遍历

「前序遍历（递归）：」

function preOrder(root) {
  if(root) {
      console.log(root.value) //这里是操作的核心，可以利用该结点值进行很多操作
      preOrder(root.left)
      preOrder(root.right)
  }
}

「中序遍历（递归）：」

function inOrder(root) {
    if(root) {
        inOrder(root.left)
        console.log(root.val)
        inOrder(root.right)
     }
}

「后序遍历（递归）：」

function postOrder(root) {
    if(root) {
        postOrder(root.left)
        postOrder(root.right)
        console.log(root.val)
     }
}

拿上面定义的二叉树tree测试一下

preOrder（tree）//依次输出ABDHIECFG
inOrder（tree）//依次输出HDIBEAFCG
postOrder（tree）//依次输出HIDEBFGCA

符合预期，顺便说句，上面三种递归遍历是利用系统栈来实现的。

非递归遍历

接下来，将会介绍非递归方法，可能理解起来会比递归难点，但要抓住核心点就会很容易写出来

「前序遍历（非递归）：」

function preOrder(root) {
   if(!root) {return false} //若根节点为空，则停止
    let stack = [] //初始化栈，用于存储已经访问过的结点，方便回溯
    let p = root //将根节点赋给p
   while(stack.length || p) { //栈不为空或p不为空，证明还没遍历完
        if(p) { //当p不为空，就一直向左走，记住是先访问了结点再将结点压栈
            console.log(p.val)
            stack.push(p)
            p = p.left
        }
        else { //当p为空，则取经过的上一个结点，然后向右走
          p = stack.pop()
          p = p.right
        }
    }
}

「中序遍历（非递归）：」

function inOrder(root) {
   if(!root) {return false} //若根节点为空，则停止
    let stack = [] //初始化栈，用于存储已经访问过的结点，方便回溯
    let p = root //将根节点赋给p
   while(stack.length || p) { //栈不为空或p不为空，证明还没遍历完
        if(p) { //当p不为空，就一直向左走，这就是与前序遍历不同的地方，这里是先压栈，取出来再访问
            stack.push(p)
            p = p.left
        }
        else { //当p为空，则取经过的上一个结点，然后向右走
          p = stack.pop()
          console.log(p.val)
          p = p.right
        }
    }
}

不知有发现了没，几乎就是跟前序遍历一毛一样了，就是差别在访问结点的时机而已。前序是先压栈再访问，中序是先压栈，后面出栈再访问。

「后序遍历（非递归）」

很多人都觉得后续遍历是最难的，确实，如果是按照左->右->根的顺序来写，会涉及到结点的访问状态的判断，会更加的复杂。但我不打算这样做，我要大家只要掌握了前序遍历非递归就能顺手的把中序后序都写出来，相信我好吗 我的想法是这样的: 「后序遍历的顺序是左->右->根对吧，那如果我先按照根->右->左的方式遍历，然后最后把结果倒置一下，不就成了左->右->根了吗」。最重要的是，如果是按照根->右->左的方式遍历，那不就是跟前序遍历是差不多的吗，也就改一两行代码的事。下面是根据上面思路整理的代码

function postOrder(root) {
   if(!root) {return false} //若根节点为空，则停止
    let stack = [] //初始化栈，用于存储已经访问过的结点，方便回溯
    let result = [] //这里保存按根->右->左访问的结果，到最后逆序输出
    let p = root //将根节点赋给p
   while(stack.length || p) { //栈不为空或p不为空，证明还没遍历完
        if(p) { //当p不为空，就一直向右走，记住是先访问了结点再将结点压栈
            result.push(p.val) //这里把结点值压栈，最会整个栈倒置输出
            stack.push(p)
            p = p.right //向右走
        }
        else { //当p为空，则取经过的上一个结点，然后向左走
          p = stack.pop()
          p = p.left
        }
    }
    result.reverse().forEach(val => console.log(val)) //逆序输出，这就是后序遍历的结果了
}

你们看，这样就简单多了吧，主要思想跟前序遍历还是差不多一样的，多了个栈来保存结果而已

好的，现在来介绍最后一个，层次遍历。层次遍历没有递归法，我们是通过一个数组模拟队列来维持访问按层访问顺序。首先将根结点入队列。当队列不为空时，执行循环体：取出队首结点，如果该节点有左子树，则将该节点的左子树存入队列；如果该节点有右子树，则将该节点的右子树存入队列。然后继续该循环，直至队列为空。

层次遍历

function floorOrder(root) {
   if(!root) {return false} //若根节点为空，则停止
    let queue = [] //初始化队列
    queue.push(root) //根节点入队
    while(queue.length) { //若队列不为空，循环体继续
        let p = queue.shift() //取队首结点赋给p，注意，出队后现在队列长度已减小1了
        console.log(p.val)
        if(p.left) { //若p的左节点不为空，则入队
            queue.push(p.left)
        }
        if(p.right) { //若p的右节点不为空，则入队
            queue.push(p.right)
        }
    }
    
}

结语

本文介绍了二叉树定义，特点，用处，结点数据结构及其前中后序的递归非递归算法、以及层次遍历算法，各位小伙伴可以拿文中的算法实现拿去跑一下是否结果正确，如果哪里有不正确的地方，热切希望小伙伴们能留言反馈下，感谢！个人认为，对于上面介绍到的遍历方式，可以当作模板去记，不理解的可以用笔画出来模拟算法的实现，画着画着你可能就懂啦！二叉树遍历是二叉树相关算法的基础，大家一定要熟练啦，一起加油！

本人个人网站： www.jianfengke.com/

本文使用 mdnice 排版