Week02 学习笔记

1 哈希表、映射、集合的实现与特性

哈希表（Hash table）也叫散列表。可以根据关键码直接访问数据。
它通过哈希函数（Hash Function）把关键码映射到表中的一个位置，来加快访问速度。
哈希碰撞工程中常用解决方式：拉链式，通过增加一个链表来实现。
平均查询时间复杂度：O(1)，如果哈希函数不好，查询则会退化到O(n)。

1.1 Java中的使用：

Map：key-value形式，key不重复，定义为一个接口
- HashMap() ，TreeMap() 二叉搜索树内部用红黑树实现
- put(key, value)
- get(key)
- containsKey(key)，containsValue(value)
- size()
- clear()
Set：不重复的元素集合，定义为一个接口
- HashSet()，TreeSet() 二叉搜索树内部用红黑树实现
- add(value)
- remove(value)
- contains(value)

1.2 HashMap 源码分析

Java中的HashSet内部是基于HashMap实现的，每次存的value是一个空的Object。所以这里我们着重看一下HashMap的源码。

参考资料：

HashMap原理深入理解

来复习一波，HashMap底层实现原理解析

JDK 源码中 HashMap 的 hash 方法原理是什么？

Java8 HashMap源码分析

put(K key, V value) 存数据

    public V put(K key, V value) {
        // 先通过hash函数算出key对应的hash值
        return putVal(hash(key), key, value, false, true);
    }

    // 优化后的hash函数，扰动函数，防止不同的hashCode的高位不同但低位相同导致的hash冲突
    static final int hash(Object key) {
        int h;
        return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
    }

    final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
        Node<K, V>[] tab;
        Node<K, V> p;
        int n, i;
        // 如果当前表为空则进行初始化 默认初始大小为1 << 4 = 16，负载因子：0.75f
        if ((tab = table) == null || (n = tab.length) == 0)
            n = (tab = resize()).length;
        // 得到要插入的位置，为null说明没有冲突，直接插入
        if ((p = tab[i = (n - 1) & hash]) == null)
            tab[i] = newNode(hash, key, value, null);
        else {
            Node<K, V> e;
            K k;
            // 如果key存在，就直接覆盖value
            if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k))))
                e = p;
                // 判断是否为红黑树
            else if (p instanceof TreeNode)
                e = ((TreeNode<K, V>) p).putTreeVal(this, tab, hash, key, value);
            else {
                // 链表
                for (int binCount = 0; ; ++binCount) {
                    if ((e = p.next) == null) {
                        // 如果e下一个节点为空，赋值给下一个节点
                        p.next = newNode(hash, key, value, null);
                        if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                            // 当链表长度大于8，改成红黑树
                            treeifyBin(tab, hash);
                        break;
                    }
                    // key相同 跳出循环
                    if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k))))
                        break;
                    p = e;
                }
            }
            if (e != null) { // existing mapping for key
                V oldValue = e.value;
                // 根据规则选择是否覆盖value
                if (!onlyIfAbsent || oldValue == null)
                    e.value = value;
                afterNodeAccess(e);
                return oldValue;
            }
        }
        ++modCount;
        // 判断是否需要扩容
        if (++size > threshold)
            resize();
        afterNodeInsertion(evict);
        return null;
    }

get(Object key) 取数据

    public V get(Object key) {
        Node<K, V> e;
        // 根据key及其hash值查询node节点，如果存在，则返回该节点的value值
        return (e = getNode(hash(key), key)) == null ? null : e.value;
    }

    // 根据key搜索节点的方法。判断key相等的条件：hash值相同并且equals()相等
    final Node<K, V> getNode(int hash, Object key) {
        Node<K, V>[] tab;
        Node<K, V> first, e;
        int n;
        K k;
        // 根据输入的hash值，可以直接计算出对应的下标，如果存在结果，则必定在table的这个位置上
        if ((tab = table) != null && (n = tab.length) > 0 && (first = tab[(n - 1) & hash]) != null) {
            // 判断第一个存在的节点的key是否和查询的key相等。如果相等，直接返回该节点
            if (first.hash == hash && // always check first node
                    ((k = first.key) == key || (key != null && key.equals(k))))
                return first;
            // 遍历该链表或红黑树直到next为null
            if ((e = first.next) != null) {
                // 为红黑树结构时，遍历红黑树节点，查看是否有匹配的TreeNode
                if (first instanceof TreeNode)
                    return ((TreeNode<K, V>) first).getTreeNode(hash, key);
                do {
                    // 为链表结构时，遍历链表，判断key是否相同
                    if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k))))
                        return e;
                } while ((e = e.next) != null);
            }
        }
        return null;
    }

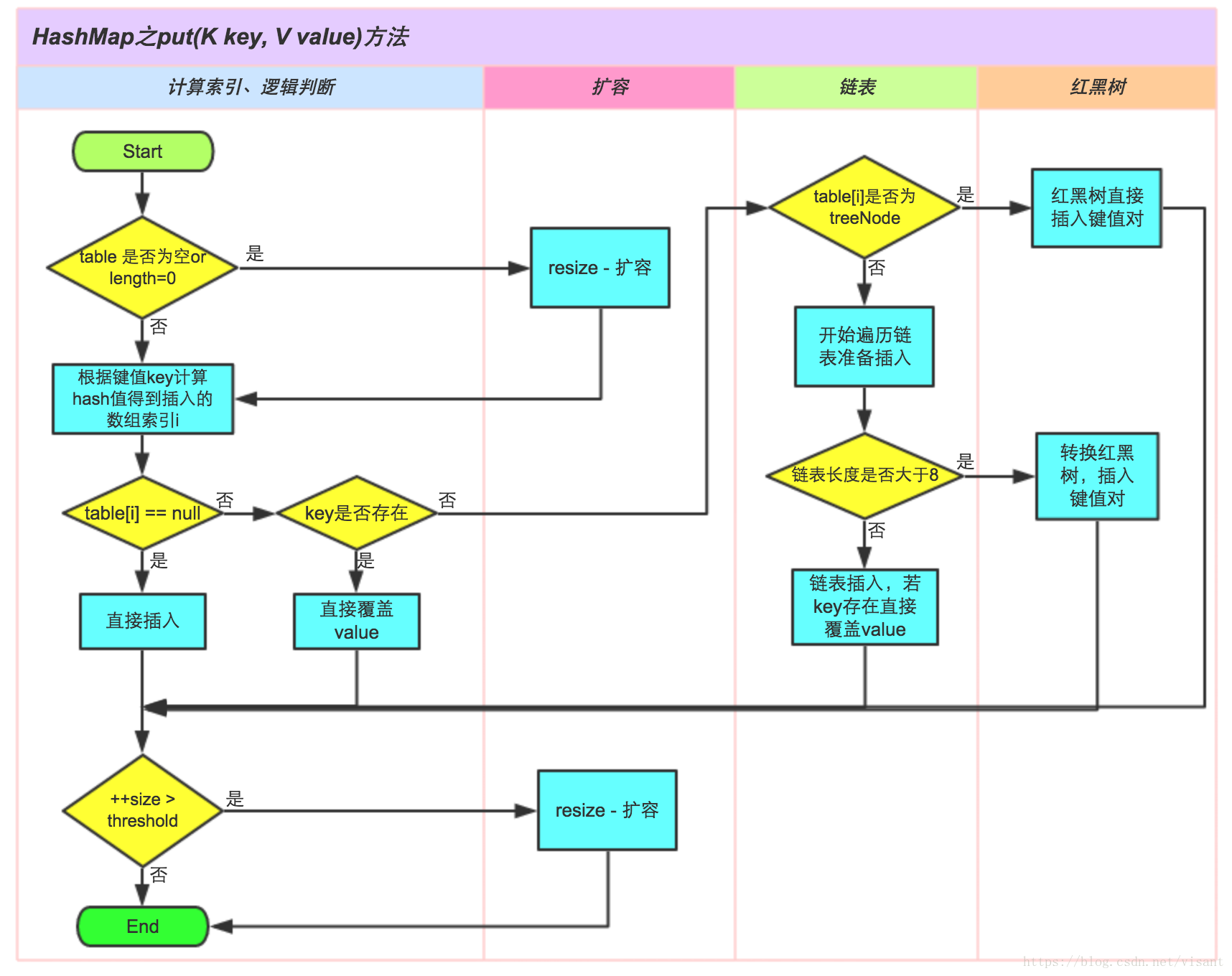
附上一张大佬博客的put方法流程图：

2 树、二叉树、二叉搜索树的实现与特性

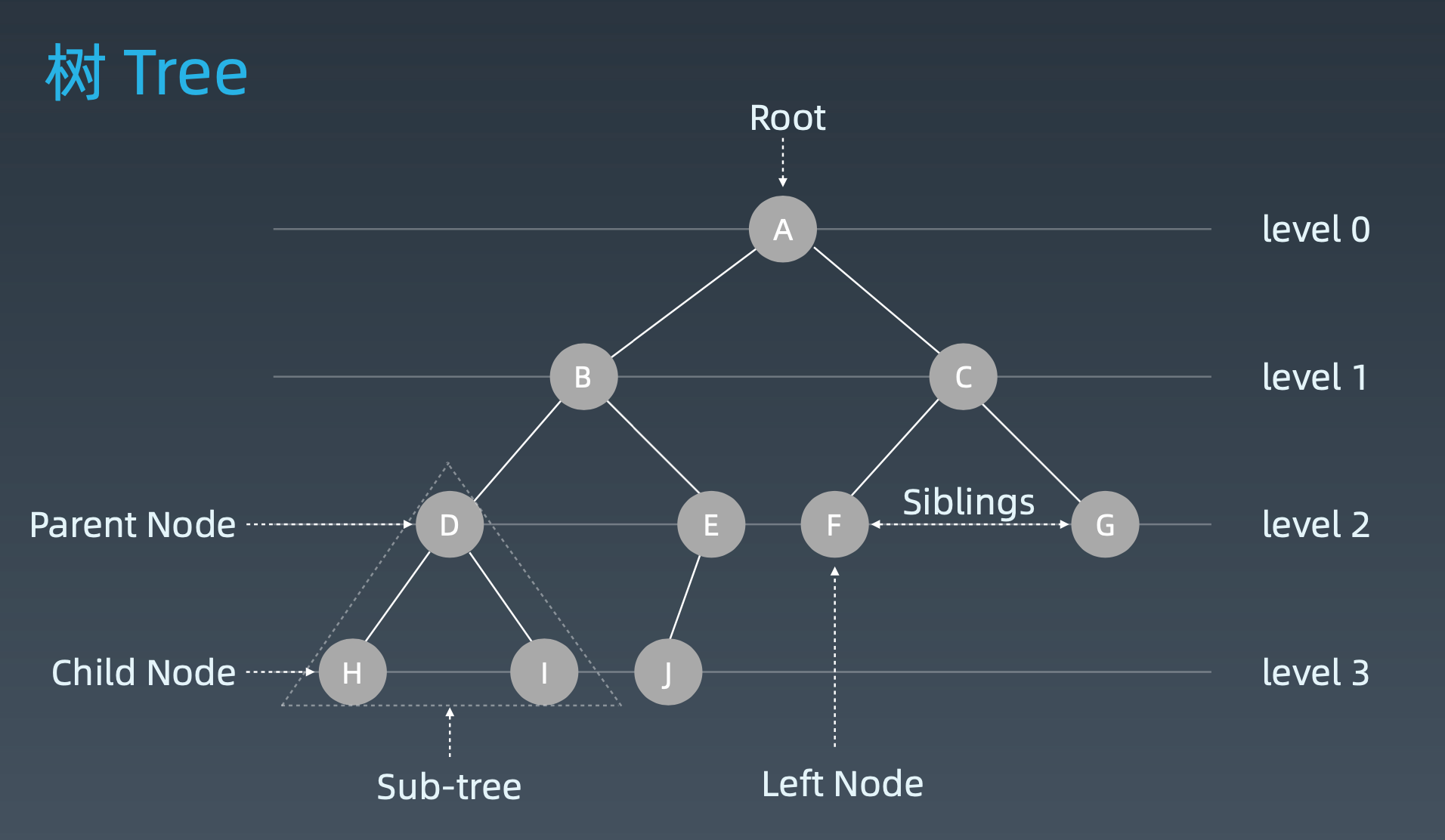
2.1 树

Linked List是一种特殊的树，每一层都只有一个子节点。

2.2 二叉树

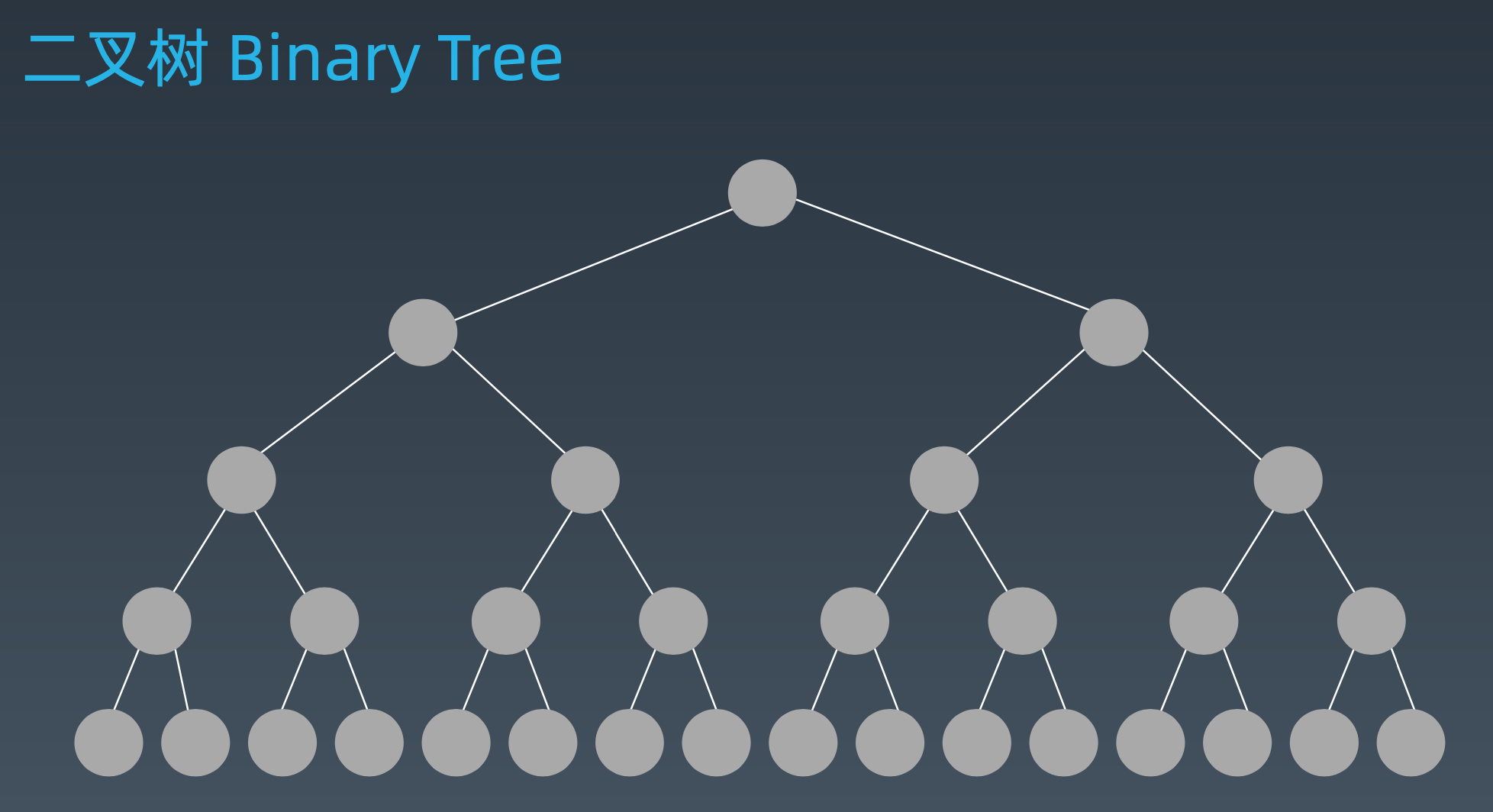
二叉树的遍历：

前序遍历：根 - 左 - 右
中序遍历：左 - 根 - 右
后序遍历：左 - 右 - 根

一般树的遍历都使用递归来实现，示例代码：

// 前序
void preorder(Node root) {
  if (root != null) {
    System.out.println(root.val);
    preorder(root.left);
    preorder(root.right);
  }
}

// 中序
void inorder(Node root) {
  if (root != null) {
    inorder(root.left);
    System.out.println(root.val);
    inorder(root.right);
  }
}

// 后序
void postorder(Node root) {
  if (root != null) {
    postorder(root.left);
    postorder(root.right);
    System.out.println(root.val);
  }
}

2.3 二叉搜索树

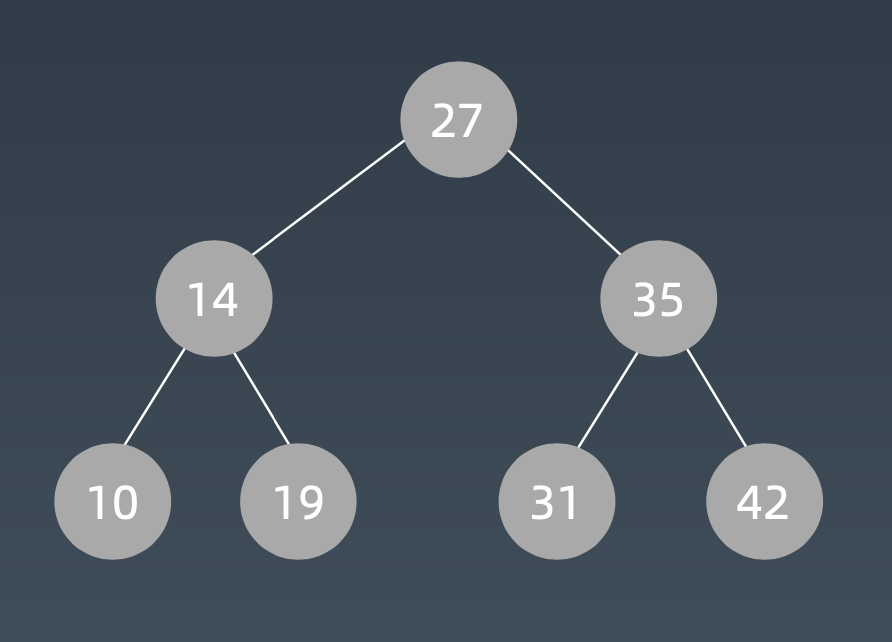
二叉搜索树特性：

左子树上所有节点值都小于根节点的值。
右子树上所有节点值都大于根节点的值。
中序遍历为升序排列
查询、插入、删除时间复杂度都为O(log n)，退化成链表时最坏O(n)

3 堆和二叉堆、图

3.1 堆

可以迅速找到一堆数中的最大值或最小值的数据结构。

如果根节点的值最大叫大顶堆，根节点的值最小叫小顶堆。

堆的实现有好多种，常见的二叉堆、斐波那契堆等。

常见操作时间复杂度：

查找最大/最小值：O(1)
删除最大/最小值：O(log n)
插入元素：O(log n)，最好情况O(1)

3.2 二叉堆

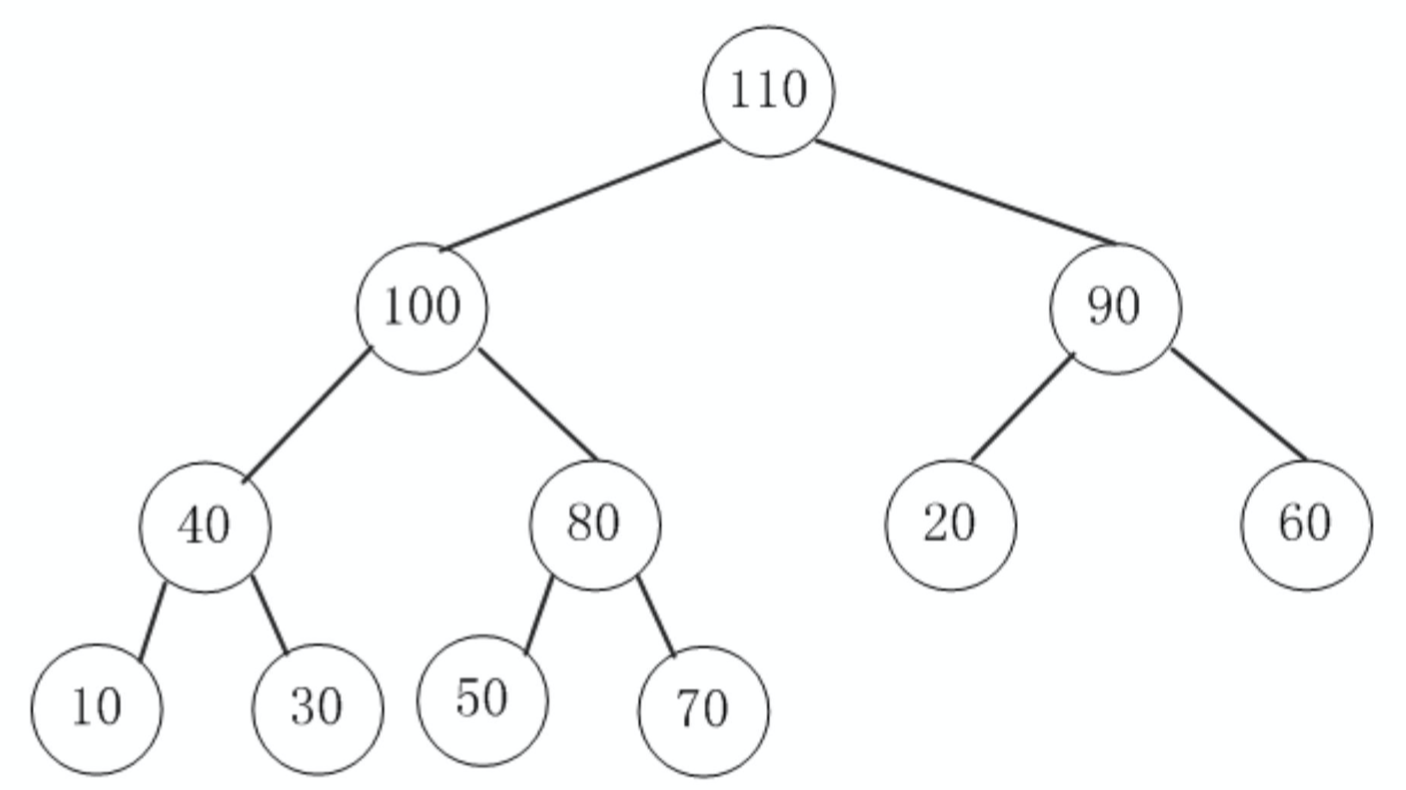
通过完全二叉树实现（不是二叉搜索树）。

性质：

是一颗完全树。
树中任意节点的值总是大于等于子节点的值。

实现：

一般通过数组实现。
假设第一个数组索引为0，父节点和子节点关系如下：
- i节点的左孩子索引为：2*i+1
- i节点的右孩子索引为：2*i+2
- i节点的父节点索引为：(i - 1) / 2 向下取整

插入操作：

新元素插入到最后面
依次向上调整整个堆的结构，直到根节点

删除最大值：

将最后面元素放到第一个位置
依次向下调整整个堆的结构，直到堆尾

堆排序示例，这里推荐一个iOS应用：算法动画图解

上面视频无法显示，可以看这里：www.bilibili.com/video/BV1HC…

3.3 图

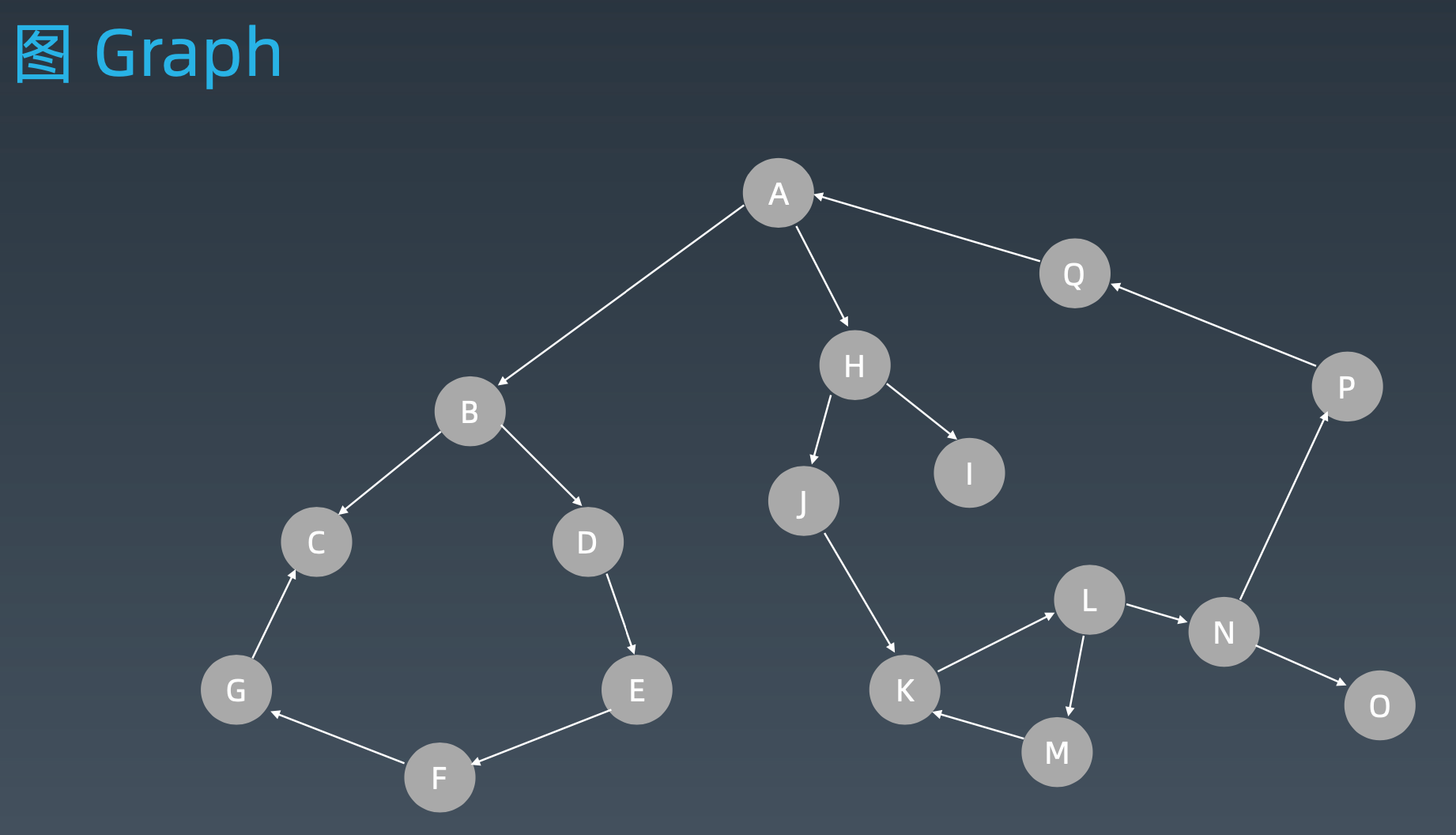
图的属性：

点 V
- 入度 - 出度
- 点与点之间是否连通
边 E
- 有向 - 无向
- 权重（边长）

常见算法：

DFS 深度优先搜索
BFS 广度优先搜索

算法训练-Week02