Week01 学习笔记
1 学习算法方法
1.1 课程学习流程
- 课前预习,把ppt先过一遍
- 倍速看视频,不懂的地方暂停反复看
- 做课后练习题,刻意练习
- 构建自己的知识图谱,逐渐完善
1.2 做题流程 五毒神掌
- 5分钟看题,不要着急做,先理解题目
- 10分钟内想不出来,看题解,理解别人的代码
- 自己写一遍,尽量不再看题解
- 自己AC之后,看国际站上的高分解题方法
- 回来自己再做一遍
- 一天后,一周后再来做一遍,忘记了就再重复一遍上面的流程,直到不看题解就能做出来
- 面试前集中过一遍
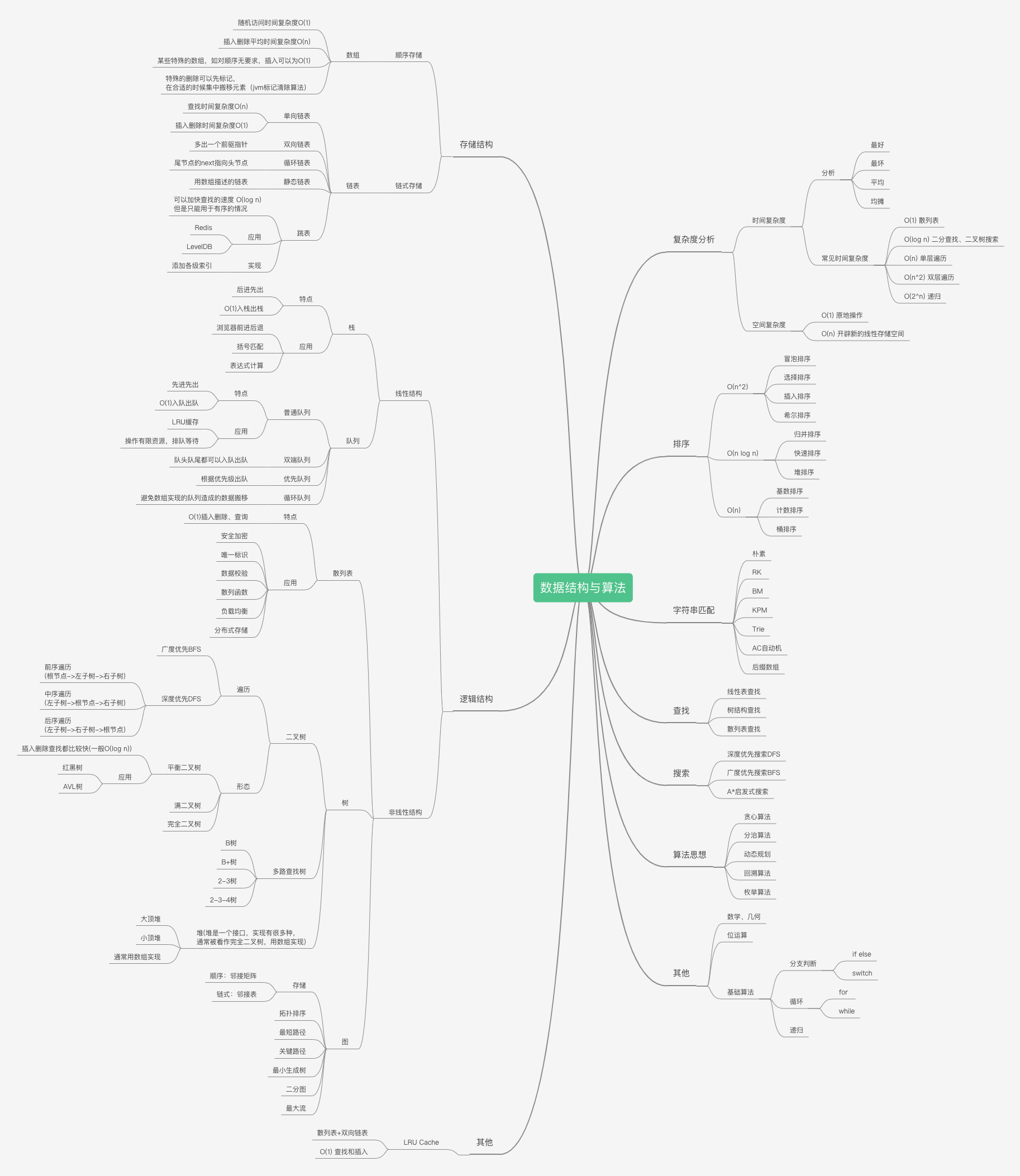
1.3 数据结构与算法脑图
2 编程习惯
- 设置好最适合自己的编程环境
- 摒弃之前的坏习惯
- 自顶向下的编程方式,结构清晰
3 复杂度分析
3.1 时间复杂度
只看最高的复杂度
常见的时间复杂度
- O(1) 常数级别,如散列表操作
- O(log n) 对数级别,如二分查找
- O(n) 线性级别,如计数排序
- O(n^2) 平方级别,如冒泡排序
- O(2^n) 指数级别,如斐波拉契递归
- O(n!) 阶乘
3.2 空间复杂度
有没有额外申请空间,原地操作为O(1)
- 数组的长度
- 递归的深度
4 数组、链表、跳表
4.1 数组
- 随机访问,O(1)时间复杂度
- 插入删除,O(n)时间复杂度 (涉及到元素的搬移)
Java中的ArrayList就是对数组的封装,默认数组大小是10, 每次插入都会进行元素的copy, 如果大小不够,就会进行扩容,申请一个当前大小二倍的空间,再把当前元素copy过去。
4.2 链表
- 查找,O(n)时间复杂度
- 插入删除,O(1)时间复杂度
Java中的LinkList使用双向链表来实现
添加节点操作
new.next = node.nextnode.next = new
删除节点操作
node.pre.next = node.nextnode.next = null
4.3 跳表
- 插入删除查找,O(log n)时间复杂度
只能用于有序列表
通过空间换时间,增加索引,优化链表的查找速度,空间复杂度O(n)
对标的是平衡树(AVL)和二分查找
实际应用有:Redis、LevelDB等
5 栈、队列、双端队列、优先队列
5.1 栈
- 后进先出
- 添加删除,O(1)时间复杂度
Java中Stack的API,其内部通过数组实现
peek()查看栈顶元素pop()出栈push(e)入栈search(e)搜索栈内元素,返回该元素在栈内的深度,即下标+1
5.2 队列
- 先进先出
- 添加删除,O(1)时间复杂度
Java中的Queue是一个接口,他的实现有好多种,如LinkedList,PriorityQueue,LinkedBlockingQueue等
| 抛出异常 | 返回值 | 说明 |
|---|---|---|
add(e) |
offer(e) |
入队 |
remove() |
poll() |
出队 |
element() |
peek() |
查看队首元素 |
5.3 双端队列
- 两端都可以进出的队列
- 添加删除,O(1)时间复杂度
Java中的Deque也是一个接口,他继承了Queue
| 抛出异常 | 返回值 | 说明 |
|---|---|---|
addFirst(e) |
offerFirst(e) |
在队头添加元素 |
addLast(e) |
offerLast(e) |
在队尾添加元素 |
getFirst() |
peekFirst() |
查看队首元素 |
getLast() |
peekLast() |
查看队尾元素 |
removeFirst() |
pollFirst() |
删除队首元素 |
removeLast() |
pollLast() |
删除队尾元素 |
5.4 优先队列
- 可以按优先级出队
- 插入,O(1)时间复杂度
- 取出,O(log n)时间复杂度
- 底层实现有:堆(heap)、二叉树搜索树(bst)等
Java中的是PriorityQueue,继承AbstractQueue,最终实现了Queue
6 本周作业
6.1 用 add first 或 add last 这套新的 API 改写 Deque 的代码
Deque<String> deque = new LinkedList<>();
// 双端队列 实现 队列 先进先出
deque.addLast("a");
deque.addLast("b");
deque.addLast("c");
System.out.println(deque);
String peek = deque.peekFirst();
System.out.println(peek);
System.out.println(deque);
while (deque.size() > 0) {
System.out.println(deque.pollFirst());
}
System.out.println(deque);
// 双端队列 实现 栈 后进先出
deque.addFirst("a");
deque.addFirst("b");
deque.addFirst("c");
System.out.println(deque);
String peek2 = deque.peekFirst();
System.out.println(peek2);
System.out.println(deque);
while (deque.size() > 0) {
System.out.println(deque.pollFirst());
}
System.out.println(deque);
6.2 分析 Queue 和 Priority Queue 的源码
6.2 .1 Queue
Java中的Queue是一个接口,继承了Collection接口
主要方法有:
// 添加一个元素,添加失败会抛出异常 IllegalStateException
boolean add(E e);
// 添加一个元素,添加失败返回false
boolean offer(E e);
// 删除队首元素,删除失败会抛出异常 NoSuchElementException
E remove();
// 删除队首元素,删除失败返回null
E poll();
// 查看队首元素,不存在则抛出异常 NoSuchElementException
E element();
// 查看队首元素,不存在返回null
E peek();
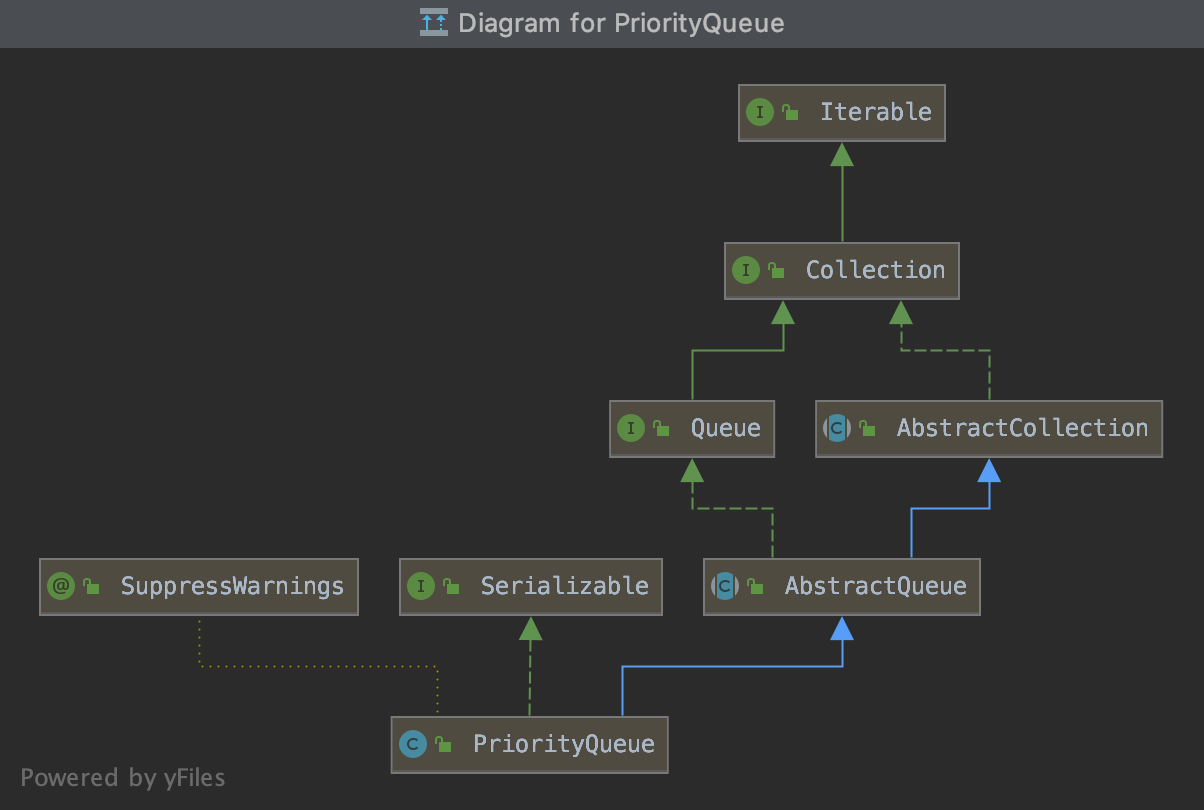
6.2.2 Priority Queue
Java中的PriorityQueue继承了AbstractQueue,类关系图如下:
主要看一下他的入队和出对方法
- 入队
offer(e)
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
// 修改次数加一,无论添加还是删除,这个值都会加一
modCount++;
int i = size;
// 判断是否需要扩容,默认数组大小是11
// 扩容会比较是否原始大小是否小于64,如果小于扩容一倍大小,否则扩容50%
if (i >= queue.length)
grow(i + 1);
siftUp(i, e);
// 大小加一
size = i + 1;
return true;
}
// 扩容
private void grow(int minCapacity) {
int oldCapacity = queue.length;
// Double size if small; else grow by 50%
int newCapacity = oldCapacity + ((oldCapacity < 64) ? (oldCapacity + 2) : (oldCapacity >> 1));
// overflow-conscious code
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
queue = Arrays.copyOf(queue, newCapacity);
}
// 将元素x插入到最小二叉堆的k位置
private void siftUp(int k, E x) {
if (comparator != null)
siftUpUsingComparator(k, x, queue, comparator);
else
siftUpComparable(k, x, queue);
}
private static <T> void siftUpComparable(int k, T x, Object[] es) {
Comparable<? super T> key = (Comparable<? super T>) x;
while (k > 0) {
// 找到插入位置的父结点
int parent = (k - 1) >>> 1;
Object e = es[parent];
// 如果插入结点比父结点大,则不用调整位置
if (key.compareTo((T) e) >= 0)
break;
// 如果插入数据比父结点大,将插入结点跟父结点数据互换
es[k] = e;
k = parent;
}
// 最后找到了调整后的位置
es[k] = key;
}
// 和siftUpComparable相同,只不过使用传入的比较器
private static <T> void siftUpUsingComparator(int k, T x, Object[] es, Comparator<? super T> cmp) {
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = es[parent];
if (cmp.compare(x, (T) e) >= 0)
break;
es[k] = e;
k = parent;
}
es[k] = x;
}
- 出队
poll()
public E poll() {
final Object[] es;
final E result;
if ((result = (E) ((es = queue)[0])) != null) {
modCount++;
final int n;
// 先减少堆大小,把最后位的数据缓存在x里
final E x = (E) es[(n = --size)];
es[n] = null;
if (n > 0) {
// 把x跟0位置及其子结点循环比较,直到x插入到了合适位置
final Comparator<? super E> cmp;
if ((cmp = comparator) == null)
siftDownComparable(0, x, es, n);
else
siftDownUsingComparator(0, x, es, n, cmp);
}
}
return result;
}
private static <T> void siftDownComparable(int k, T x, Object[] es, int n) {
// assert n > 0;
Comparable<? super T> key = (Comparable<? super T>)x;
int half = n >>> 1; // loop while a non-leaf
while (k < half) {
int child = (k << 1) + 1; // assume left child is least
Object c = es[child];
int right = child + 1;
if (right < n && ((Comparable<? super T>) c).compareTo((T) es[right]) > 0)
c = es[child = right];
if (key.compareTo((T) c) <= 0)
break;
es[k] = c;
k = child;
}
es[k] = key;
}
private static <T> void siftDownUsingComparator(
int k, T x, Object[] es, int n, Comparator<? super T> cmp) {
// assert n > 0;
int half = n >>> 1;
while (k < half) {
int child = (k << 1) + 1;
Object c = es[child];
int right = child + 1;
if (right < n && cmp.compare((T) c, (T) es[right]) > 0)
c = es[child = right];
if (cmp.compare(x, (T) c) <= 0)
break;
es[k] = c;
k = child;
}
es[k] = x;
}