DailyChallenge

84柱状图中最大的矩形

20200530

难度：困难

题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

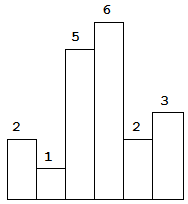
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

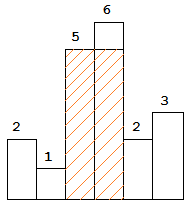
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

Solution

思路一

暴力法遍历。对每个高度，分别向左右扩展，求这个高度对应的最大宽度，然后更新面积，求最大。

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        if(n == 0){
            return 0;
        }
        int res = 0;
        for(int i = 0; i < n; i++){
            int height = heights[i];
            //找左边
            int left = i;
            while(left >= 0 && heights[left] >= height){
                left--;
            }
            //找右边
            int right = i;
            while(right < n && heights[right] >= height){
                right++;
            }
            int wide = right - left - 1;
            res = Math.max(res, wide * height);
        }
        return res;
    }
}

复杂度分析：

• 时间复杂度：O(N^2)，这里 N是输入数组的长度。
• 空间复杂度：O(1)。

思路二

单调栈 + 加入哨兵

遍历的时候，记录下标，如果当前的高度比它之前的高度严格小于的时候，就可以直接确定之前的那个高的柱形的最大矩形的面积。

维护一个单调栈，栈中总是保存递增元素的索引，当遇到比栈顶元素小的元素时，将栈顶元素依次出栈，每次都计算栈中的bar能围成的面积，直到栈顶元素小于当前元素就停止出栈。

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        if(n == 0) return 0;
        if(n == 1) return heights[0];
        int res = 0;
        // 放入左右两个哨兵
        int[] newHeights = new int[n + 2];
        newHeights[0] = 0;
        System.arraycopy(heights, 0, newHeights, 1, n);
        newHeights[n+1] = 0;
        n += 2;
        heights = newHeights;

        Deque<Integer> stack = new ArrayDeque<>(n);
        stack.addLast(0);//放入哨兵
        for(int i = 1; i < n; i++){
            while(heights[i] < heights[stack.peekLast()]){
                int curHeight = heights[stack.pollLast()];
                int curWidth = i - stack.peekLast() - 1;
                res = Math.max(res, curHeight * curWidth);
            }
            stack.addLast(i);
        }
        return res;
    }
}

Tips:

1. 对于使用 Java 的朋友， Stack 改用 Deque 的问题，可以参考 Java 程序员，别用 Stack？！
2. 数组复制System.arraycopy(源数组，源数组的起始位置，目标数组，目标数组的起始位置，复制长度)

本文使用 mdnice 排版