1.简介

在有⼀个表示工程的有向图中, ⽤顶点表示活动, ⽤弧表示活动之间的优先关系,这样的网我们称为AOV⽹(Activity On Vertex Network)。

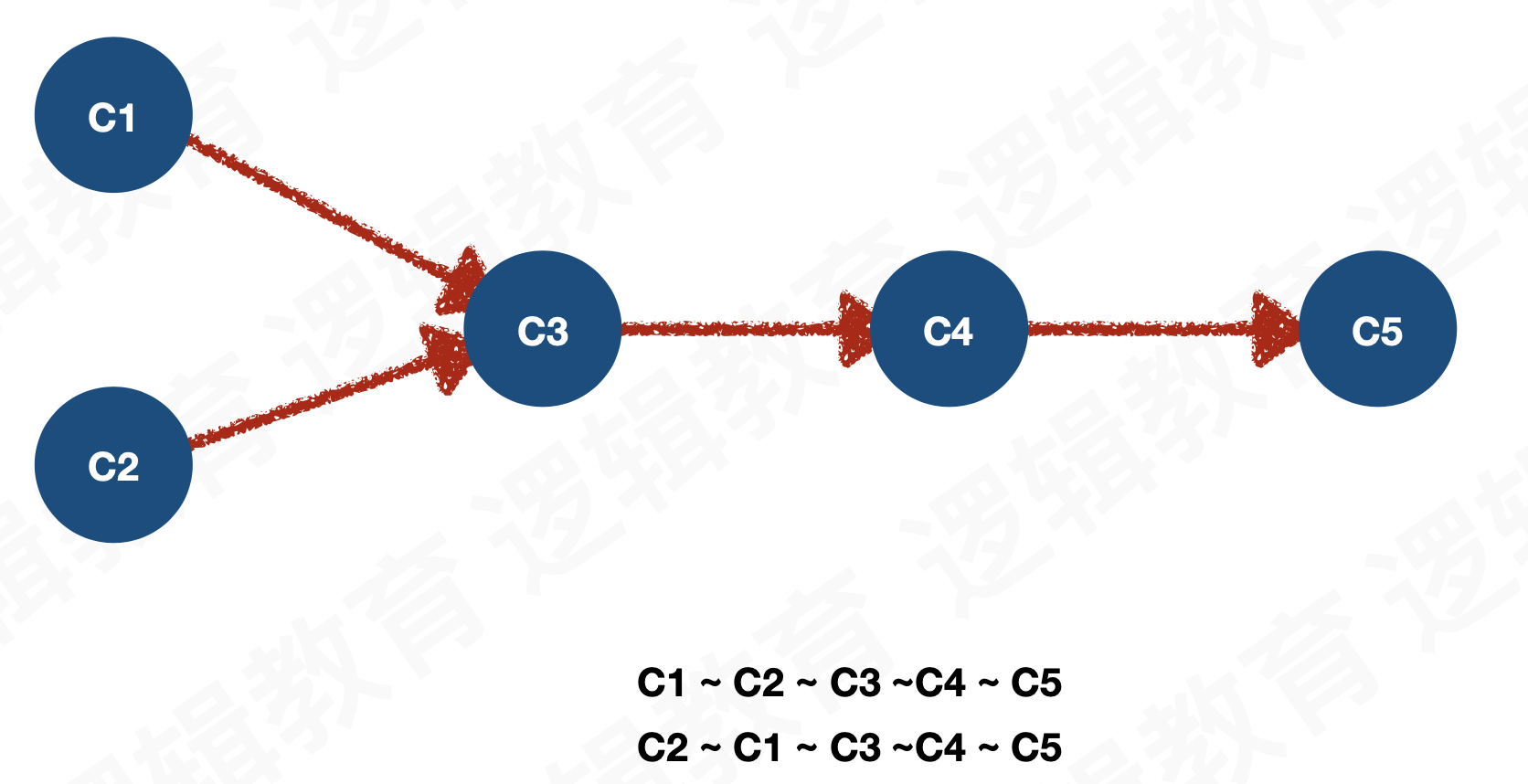
设G = (V,E)是一个具有n个顶点的有向图, V中的顶点序列V1,V2,.....,Vn.若满⾜足从顶点Vi 到Vj有⼀条路路径,则在顶点序列列Vi 必须在Vj 之前, 则我们称这样的顶点序列列成为拓扑序列。

所谓拓扑排序,其实就是对⼀个有向图构造拓扑序列的过程. 构造过程拓扑序列会产生2个结果:

如果此⽹中的全部顶点被输出,则说明它是一个不存在环(回路)的AOV网;
如果输出的顶点数少了,哪怕仅少了了一个,也说明这个网存在环(回路),不是AOV⽹。

2.实现过程

对有向无环图进行拓扑排序，只需要遵循两个原则：

在图中选择一个没有前驱的顶点 V；
从图中删除顶点 V 和所有以该顶点为尾的弧。

在这个算法实现过程,我们需要借助一个数据结构栈.来帮助我们解决避免每次查找时, 都要去遍历AOV图中的顶点表查找有没有入度为0的顶点.

创建⼀个栈(stack),⽤用来存储⼊入度in为0 的顶点序号;
遍历AOV图中顶点表,判断⼊度为0的顶点全部入栈;

2.代码实现

结构定义

/* Status是函数的类型,其值是函数结果状态代码，如OK等 */
typedef int Status;

/*邻接矩阵结构 */
typedef struct
{
    int vexs[MAXVEX];
    int arc[MAXVEX][MAXVEX];
    int numVertexes, numEdges;
}MGraph;


/* 邻接表结构****************** */
//边表结点
typedef struct EdgeNode
{
    //邻接点域，存储该顶点对应的下标
    int adjvex;
    //用于存储权值，对于非网图可以不需要
    int weight;
    //链域，指向下一个邻接点
    struct EdgeNode *next;
}EdgeNode;

//顶点表结点
typedef struct VertexNode
{
    //顶点入度
    int in;
    //顶点域，存储顶点信息
    int data;
    //边表头指针
    EdgeNode *firstedge;
}VertexNode, AdjList[MAXVEX];

//图结构
typedef struct
{
    AdjList adjList;
    //图中当前顶点数和边数
    int numVertexes,numEdges;
}graphAdjList,*GraphAdjList;

拓扑排序实现

/拓扑排序. 若AOV网图无回路则输出拓扑排序的序列并且返回状态值1,若存在回路则返回状态值0*/
/*拓扑排序:解决的是一个工程能否顺序进行的问题!*/
Status TopologicalSort(GraphAdjList GL){
    
    EdgeNode *e;
    int i,k,gettop;
    //用于栈指针下标
    int top=0;
    //用于统计输出顶点的个数
    int count=0;
    
    //建栈将入度为0的顶点入栈(目的:为了避免每次查找时都要遍历顶点表查找有没有入度为0的顶点)
    int *stack=(int *)malloc(GL->numVertexes * sizeof(int) );
    
    //1.遍历邻接表-顶点表,将入度in为0的顶点入栈
    /*参考图1> 此时stack栈中应该成为0,1,3.即V0,V1,V3的顶点入度为0*/
    for(i = 0; i<GL->numVertexes; i++)
        //将入度为0的顶点入栈
        if(0 == GL->adjList[i].in)
            stack[++top]=i;
    printf("top = %d\n",top);
    
    //2.循环栈结构(当栈中有元素则循环继续)
    while(top!=0)
    {
        //出栈
        gettop=stack[top--];
        printf("%d -> ",GL->adjList[gettop].data);
        
        //输出顶点，并计数
        count++;
        
        //遍历与栈顶相连接的弧
        for(e = GL->adjList[gettop].firstedge; e; e = e->next)
        {
            //获取与gettop连接的顶点
            k=e->adjvex;
            
            //1.将与gettop连接的顶点入度减1;
            //2.判断如果当前减1后为0,则入栈
            if( !(--GL->adjList[k].in) )
                //将k入栈到stack中,并且top加1;
                stack[++top]=k;
        }
    }
    
    printf("\n");
    
    //判断是否把所有的顶点都输出. 则表示找到了拓扑排序;
    if(count < GL->numVertexes)
        return ERROR;
    else
        return OK;
}

数据结构与算法——拓扑排序

1.简介

2.实现过程

2.代码实现