数据结构和算法五（二叉树）

二叉树新建

function Node(data, left, right) {
    this.data = data;
    this.left = left;
    this.right = right;
}

Node.prototype = {
    show: function () {
        console.log(this.data);
    }
}

function Tree() {
    this.root = null;
}

Tree.prototype = {
    insert: function (data) {
        var node = new Node(data, null, null);
        if (!this.root) {
            this.root = node;
            return;
        }
        var current = this.root;
        var parent = null;
        while (current) {
            parent = current;
            if (data < parent.data) {
                current = current.left;
                if (!current) {
                    parent.left = node;
                    return;
                }
            } else {
                current = current.right;
                if (!current) {
                    parent.right = node;
                    return;
                }
            }

        }
    },
    preOrder: function (node) {
        if (node) {
            node.show();
            this.preOrder(node.left);
            this.preOrder(node.right);
        }
    },
    middleOrder: function (node) {
        if (node) {
            this.middleOrder(node.left);
            node.show();
            this.middleOrder(node.right);
        }
    },
    laterOrder: function (node) {
        if (node) {
            this.laterOrder(node.left);
            this.laterOrder(node.right);
            node.show();
        }
    },
    getMin: function () {
        var current = this.root;
        while(current){
            if(!current.left){
                return current;
            }
            current = current.left;
        }
    },
    getMax: function () {
        var current = this.root;
        while(current){
            if(!current.right){
                return current;
            }
            current = current.right;
        }
    },
    getDeep: function (node,deep) {
        deep = deep || 0;
        if(node == null){
            return deep;
        }
        deep++;
        var dleft = this.getDeep(node.left,deep);
        var dright = this.getDeep(node.right,deep);
        return Math.max(dleft,dright);
    }
}

var t = new Tree();
t.insert(3);
t.insert(8);
t.insert(1);
t.insert(2);
t.insert(5);
t.insert(7);
t.insert(6);
t.insert(0);
console.log(t);
// t.middleOrder(t.root);
console.log(t.getMin(), t.getMax());
console.log(t.getDeep(t.root, 0));
console.log(t.getNode(5,t.root));

二叉树查找

递归法查找

• 先从根节点查找
• 如果目标值等于根节点的值，返回
• 如果目标值小于根节点的值，则去左子树找
• 如果目标值大于根节点的值，则去右子树找
• 依次把左子树和右子树当作根节点递归查找

/**
* data 目标值
* node 树
**/
function getNode(data,node){
    if(node){
        if(data == node.data){
            return node;
        }else if(data < node.data){
           return getNode(data,node.left)
        }else if(data > node.data){
            return getNode(data,node.right)
        }
    }else{
        return null;
    }
}

二分查找

• 二分查找的条件是必须是有序的线性表。
• 和线性表的中点值进行比较，如果小就继续在小的序列中查找，如此递归直到找到相同的值

/**
* data 目标值
* arr 有序线性表
* start 开始的index
* end 结束的index
**/
function binarySearch(data, arr, start, end) {
    if (start > end) {
        return -1;
    }
    var mid = Math.floor((end + start) / 2);
    if (data == arr[mid]) {
        return mid;
    } else if (data < arr[mid]) {
        return binarySearch(data, arr, start, mid - 1);
    } else {
        return binarySearch(data, arr, mid + 1, end);
    }
}
var arr = [0, 1, 1, 1, 1, 1, 4, 6, 7, 8]
console.log(binarySearch(1, arr, 0, arr.length-1));

二叉树遍历

先序(根->左->右)，中序(左->根->右)，后序(左->右->根)。如果访问有孩子的节点，先处理孩子的，随后返回

无论先中后遍历，每个节点的遍历如果访问有孩子的节点，先处理孩子的

以下边的二叉树为例

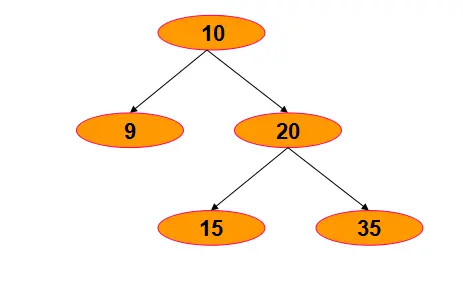
前序遍历

根节点——左子树——右子树

图上的输出顺序为 10-9-20-15-35

递归实现

function preOrder(root,array=[]){
    if(root){
        array.push(root.val);
        preOrder(root.left,array);
        preOrder(root.right,array)
    }
    return arrag;
}

非递归实现

• 取跟节点为目标节点，开始遍历
• 1.访问目标节点
• 2.左孩子入栈 -> 直至左孩子为空的节点
• 3.节点出栈，以右孩子为目标节点，再依次执行1、2、3

var preorderTraversal = function (root) {
  const result = [];
  const stack = [];
  let current = root;
  while (current || stack.length > 0) {
    while (current) {
      result.push(current.val);
      stack.push(current);
      current = current.left;
    }
    current = stack.pop();
    current = current.right;
  }
  return result;
};

中序遍历

左子树——根节点——右子树 图上的输出顺序为 9-10-15-20-35

访问完10节点过后，去找的是20节点，但20下还有子节点，因此先访问的是20的左儿子15节点。由于15节点没有儿子了。所以就返回20节点，访问20节点。最后访问35节点

递归实现

function inOrder(root,array=[]){
    if(root){
        inOrder(root.left,array)
        array.push(root.val)
        inOrder(root.right,array)
    }
    return array;
}

非递归实现

• 取跟节点为目标节点，开始遍历
• 1.左孩子入栈 -> 直至左孩子为空的节点
• 2.节点出栈 -> 访问该节点
• 3.以右孩子为目标节点，再依次执行1、2、3

var inorderTraversal = function (root) {
  const result = [];
  const stack = [];
  let current = root;
  while (current || stack.length > 0) {
    while (current) {
      stack.push(current);
      current = current.left;
    }
    current = stack.pop();
    result.push(current.val);
    current = current.right;
  }
  return result;
};

后序遍历

左子树——右子树——根节点 图上的输出顺序为 9-35-15-20-10

先访问9节点，随后应该访问的是20节点，但20下还有子节点，因此先访问的是20的左儿子15节点。由于15节点没有儿子了。所以就去访问35节点，由于35节点也没有儿子了，所以返回20节点，最终返回10节点

递归实现

var postorderTraversal = function (root, array = []) {
  if (root) {
    postorderTraversal(root.left, array);
    postorderTraversal(root.right, array);
    array.push(root.val);
  }
  return array;
};

非递归实现

• 取跟节点为目标节点，开始遍历
• 1.左孩子入栈 -> 直至左孩子为空的节点
• 2.栈顶节点的右节点为空或右节点被访问过 -> 节点出栈并访问他，将节点标记为已访问
• 3.栈顶节点的右节点不为空且未被访问，以右孩子为目标节点，再依次执行1、2、3

var postorderTraversal = function (root) {
  const result = [];
  const stack = [];
  let last = null; // 标记上一个访问的节点
  let current = root;
  while (current || stack.length > 0) {
    while (current) {
      stack.push(current);
      current = current.left;
    }
    current = stack[stack.length - 1];
    if (!current.right || current.right == last) {
      current = stack.pop();
      result.push(current.val);
      last = current;
      current = null; // 继续弹栈
    } else {
      current = current.right;
    }
  }
  return result;
}