计算机中绘制曲线，通过贝塞尔曲线已经满足了我们大部分需求，但是其存在某些缺点，比如移动某一个控制点会导致整个曲线发生变化，即无法局部控制曲线的走向。所以 B 样条曲线(B-Spline)为了解决贝塞尔曲线的缺陷应运而生。
不了解贝塞尔曲线的同学，可以去看我以前写的另外一篇文章《深入理解贝塞尔曲线》，后面的内容会假设你已经了解并掌握贝塞尔曲线的相关内容。
什么是 B 样条曲线？
解释 B 样条曲线之前，首先要解释一下什么是样条。样条是通过一组指定点集而生成平滑曲线的柔性带。 简单地说，B 样条曲线就是通过控制点局部控制形状的曲线。不太理解的同学可以通过本文底部的 demo 查看 B 样条曲线中，控制点对曲线绘制的影响。
B 样条曲线比贝塞尔曲线的设计要复杂许多，我们先通过他们的公式大致比较一下贝塞尔曲线与 B 样条曲线的区别：
贝塞尔曲线:
B 样条曲线:
先简单介绍一下上述公式的组成：
表示曲线上的点坐标向量。
为控制点
数量。
从 0 开始)。
为控制点坐标影响权重的多项式系数（式中
影响 B 样条曲线的次数：
就是曲线的次数。
是绘制曲线时的取值。
仔细观察这两个公式，我们可以看到以下的相同点：
- 都是求和公式。
- 都有一个
的多项式系数（式中贝塞尔曲线 x=n，B 样条曲线 x=d）。
可以看出有以下几个不同点：
- 贝塞尔曲线的多项式幂数与控制点数量一致，而 B 样条曲线的多项式幂数更自由。
- 贝塞尔曲线
，而 B 样条曲线是在最大和最小节点值之间。
计算多项式
公式中其他值其实都比较清晰，问题的关键是需要搞清楚那个多项式是什么！
计算这个多项式，我们使用到了Cox-deBoor 递归公式，公式内容如下（需要注意一点，如果遇到分母为 0的情况时，需要特殊处理为整体值为 0）：
从这个公式可以看出，递归公式的差异主要体现在和
的取值上。需要注意的是节点的数量是由参数
和
决定的，数量等于
。根据这些节点
的取值，可以划分为一下三种类型：
- 均匀周期性(uniform)
- 开放均匀性(open uniform)
- 非均匀性(non-uniform)
想必大家现在已经非常头晕了吧 🤪，这都什么乱七八糟的，全是公式，完全看不懂啊！如果想讲清楚 B 样条曲线是非常困难的，因为其种类繁多，参数控制也非常自由。所以我还是通过讲解计算过程的栗子 🌰 来让大家更好地理解吧！
种类一: 均匀周期性 B 样条曲线
顾名思义，均匀周期性 B 样条曲线，就是节点取值是均匀的，比如
[-1, -0.5, 0, 0.5, 1]，只要每个相邻的值间隔是相同的就可以了。不过为了方便计算，一般取值都是从 0 开始，并且间隔为 1。比如[0, 1, 2, 3, 4, 5, 6, 7, 8]。
均匀取节点值会导致每个多项式函数是周期性分布的，下面我会通过一个均匀二次 B 样条的计算过程，帮助大家理解这个周期性。
1.确定公式参数
因为是二次 B 样条曲线，所以我们可以确定以下参数：
- 曲线为二次，所以
，所以
。
- 控制点数量我们手动取值为 4（也可以取值为其他的值），即
。
- 节点
的数量为
，取值为 7，所以节点范围为：
[0, 1, 2, 3, 4, 5, 6]。
确定这几个值后，我们就可以开始计算多项式 B 的值了。下面是迭代公式：
2.计算常量值的多项式
首先根据上面的公式 1，我们可以先得出常量值的多项式、
、
、
:
时：
时：
时：
时：
因为 B 样条曲线公式为：
从上式可以很轻松地看出，我们需要知道以下几个多项式的函数：
所以我们现在依次求解这些多项式的函数。
3.计算非常量的多项式
求)
的值（即
）：
从上式中得出，我们需要得到和
的值。
求)
的值（即
）：
求)
的值（即
）：
得出)
继续迭代，我们就可以得出了:
求)
, )
, )
的值
这三个多项式的求解过程与一致，有兴趣的小伙伴可以自己计算一下，加深理解。这里我仅给出最后的结果。
将四个函数分别绘制到坐标系中，大家就可以看到图像形状是完全相同的，只是在 x 轴方向做了平移，如下图所示。
:
:
:
:
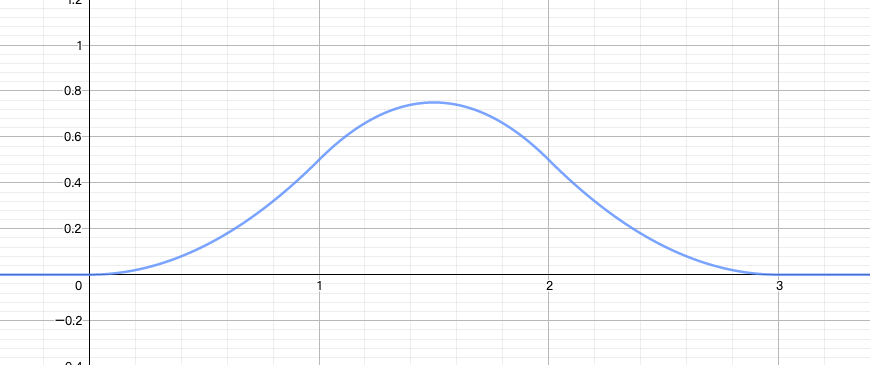
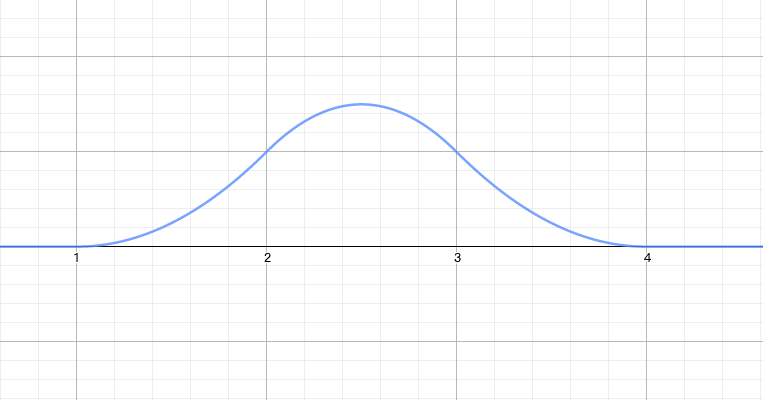
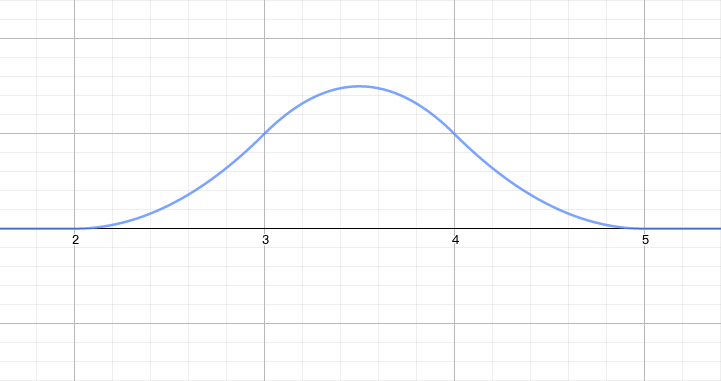
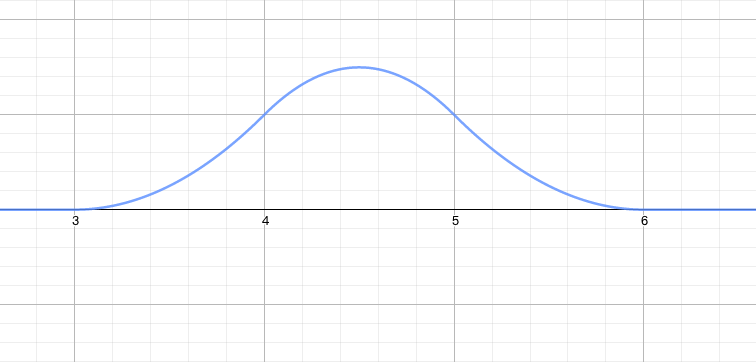
4.确定曲线方程。
之前已经计算出了曲线的方程式，如下：
将上面的多项式带入到方程，就可以得到最终的曲线方程。然后将 t 从 0 取至 6，获得的点集就是我们想要的均匀周期性 B 样条曲线。
从多项式的取值，我们就可以看出 B 样条曲线的一个特点，就是控制点不会影响整个曲线的绘制，只是局部影响曲线的走向。
最后
我写了一个线上的demo，用于展示均匀周期性 B 样条曲线的绘制，有兴趣的同学可以去看一下。
下篇我将会介绍剩下两种 B 样条曲线的绘制过程，敬请期待！
