-
AOV网概念
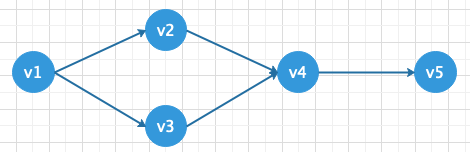
有一个表示工程的有向图中, 用顶点表示活动, 用弧表示活动之间的优先关系,这样 有向图为顶点表示活动的网. 我们称为AOV网(Activity On Vertex Network).
-
拓扑排序的简介
设G = (V,E)是一个具有n个顶点的有向图, V中的顶点序列V1,V2,.....,Vn.若满足从顶点Vi 到Vj有一条路径,则在顶点序列Vi 必须在Vj 之前, 则我们称这样的顶点序列成为拓扑序列 所谓拓扑排序,其实就是对一个有向图构造拓扑序列的过程. 构造过程拓扑序列会产生2个结果:
-
如果此网中的全部顶点被输出,则说明它不存在环(回路)的AOV⽹;
-
如果输出的顶点数少了,哪怕仅少了一个,也说明这个网存在环(回路),不是AOV⽹
举个例子(学习Metal的列子): 首先要学会OpenGL基础和3D数学,然后才能学习OpenGL ES 学会了OpenGL ES才能学习GPUImage 然后才能学习Metal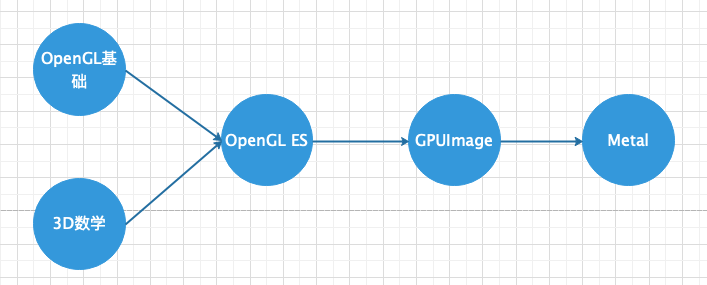
-
-
拓扑排序的实现思路
创建一个栈stack 将所有的入度为0的顶点入栈,然后进入下一个阶段先出栈,然后删除栈顶顶元素的所有弧信息,如果有 入度为0 的顶点继续入栈,同时还要记录出栈元素的个数用于判断符合拓扑拍讯(出栈的个数=顶点的个数)
-
实现步骤
对下图进行拓扑排序
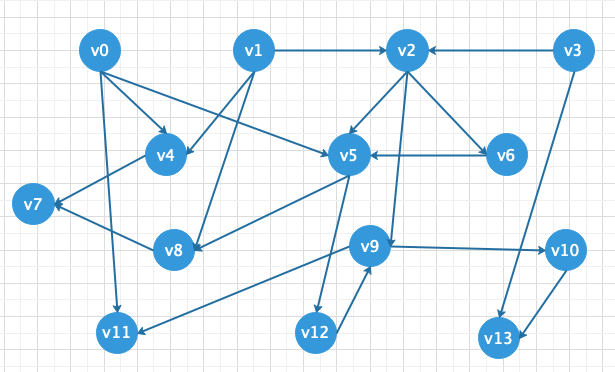
- 循环所有的顶点找到入度为0的点然后索引入栈
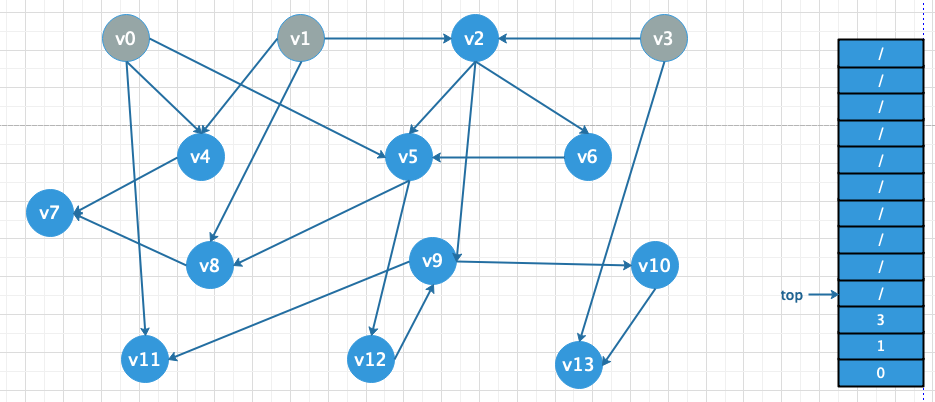
- 开始出栈(直到栈为空)并将栈顶元素对应的弧信息删除(其实就是将和栈顶顶点指向的顶点入度减一)然后在判断这些顶点的入度是否为0,为0在入站例如下图
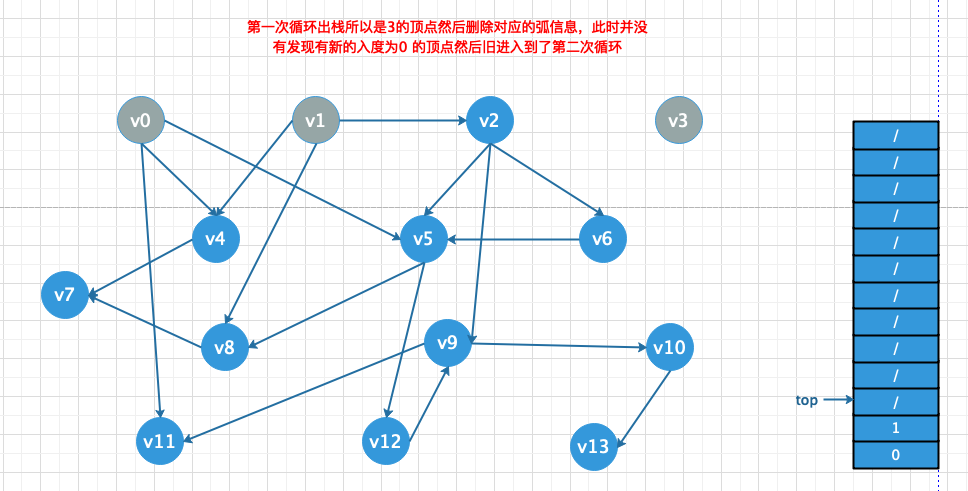
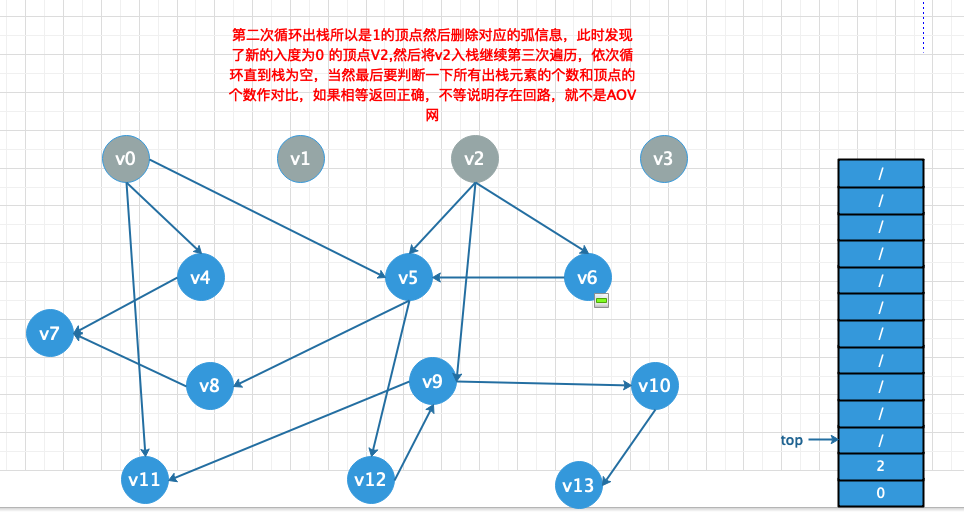
- 循环所有的顶点找到入度为0的点然后索引入栈
-
实现代码
#include <stdio.h> #include "stdlib.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXVEX 14 /* 最大顶点数,应由用户定义 */ #define MAXEDGE 20 #define INFINITYC 65535 typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ typedef char ElemType; /*邻接矩阵结构 */ typedef struct { int vexs[MAXVEX]; int arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; }MGraph; typedef struct EdgeNode{ struct EdgeNode *next; int weight; // 权重 int index; //索引 }EdgeNode; typedef struct { int data; int in; // 入度 EdgeNode * firstNode; }vertexNode,AdjList[MAXVEX]; //图结构 typedef struct { AdjList adjList; //图中当前顶点数和边数 int numVertexes,numEdges; }graphAdjList,*GraphAdjList; /*1.构成AOV网图*/ void CreateMGraph(MGraph *G)/* 构件图 */ { int i, j; /* printf("请输入边数和顶点数:"); */ G->numEdges=MAXEDGE; G->numVertexes=MAXVEX; /* 初始化图 */ for (i = 0; i < G->numVertexes; i++) { G->vexs[i]=i; } /* 初始化图 */ for (i = 0; i < G->numVertexes; i++) { for ( j = 0; j < G->numVertexes; j++) { G->arc[i][j]=0; } } G->arc[0][4]=1; G->arc[0][5]=1; G->arc[0][11]=1; G->arc[1][2]=1; G->arc[1][4]=1; G->arc[1][8]=1; G->arc[2][5]=1; G->arc[2][6]=1; G->arc[2][9]=1; G->arc[3][2]=1; G->arc[3][13]=1; G->arc[4][7]=1; G->arc[5][8]=1; G->arc[5][12]=1; G->arc[6][5]=1; G->arc[8][7]=1; G->arc[9][10]=1; G->arc[9][11]=1; G->arc[10][13]=1; G->arc[12][9]=1; } /*2.将AOV网图借助邻近矩阵转换成邻接表结构*/ void CreateALGraph(MGraph G,GraphAdjList *GL) { *GL = (GraphAdjList)malloc(sizeof(graphAdjList)); (*GL)->numVertexes = G.numVertexes; (*GL)->numEdges = G.numEdges; //初始化(默认d入度都是0) for(int i = 0; i < G.numVertexes; i ++){ (*GL)->adjList[i].data = G.vexs[i]; (*GL)->adjList[i].in = 0; (*GL)->adjList[i].firstNode = NULL; } EdgeNode *node; for(int i = 0; i < G.numVertexes; i ++){ for(int j = 0; j < G.numVertexes; j ++){ if(G.arc[i][j] == 1){ //存在指向关系 node = (EdgeNode *)malloc(sizeof(EdgeNode)); node->index = j; node->weight = 1; node->next = (*GL)->adjList[i].firstNode; (*GL)->adjList[i].firstNode = node; //对应入度要加一 (*GL)->adjList[j].in++; } } } } /*3.拓扑排序. 若AOV网图无回路则输出拓扑排序的序列并且返回状态值1,若存在回路则返回状态值0*/ /*拓扑排序:解决的是一个工程能否顺序进行的问题!*/ /* 思路:创建一个栈stack 将所有的入度为0的顶点入栈,然后进入下一个阶段先出栈,然后删除栈顶顶元素的所有弧信息,如果有 入度为0 的顶点继续入栈,同时还要记录出栈元素的个数用于判断符合拓扑拍讯(出栈的个数=顶点的个数) **/ Status TopologicalSort(GraphAdjList GL){ //初始化栈 int stack[GL->numVertexes]; int top = 0; //入度为0 的点入栈 for(int i = 0; i < GL->numVertexes; i ++){ if(GL->adjList[i].in == 0){ stack[top ++] = i; } } int count = 0; //开始出栈 while (top > 0) { //删除栈顶元素对应的弧信息(也就是对应的顶点的入度减一) printf("%d -> ",stack[--top]); count ++; EdgeNode *node = GL->adjList[stack[top]].firstNode; while (node) { GL->adjList[node->index].in --; if(GL->adjList[node->index].in == 0){ //入栈 stack[top++] = node->index; } node = node->next; } } if(count == GL->numVertexes){ return OK; } return ERROR; } int main(int argc, const char * argv[]) { // insert code here... printf("Hello, World!\n"); GraphAdjList GL; MGraph G; CreateMGraph(&G); CreateALGraph(G, &GL); TopologicalSort(GL); return 0; }