1.哈夫曼思考
假设我们根据学生的成绩分数划分成绩的等级,规则如下:

其判断的过程可以用如下树形结构来表示:
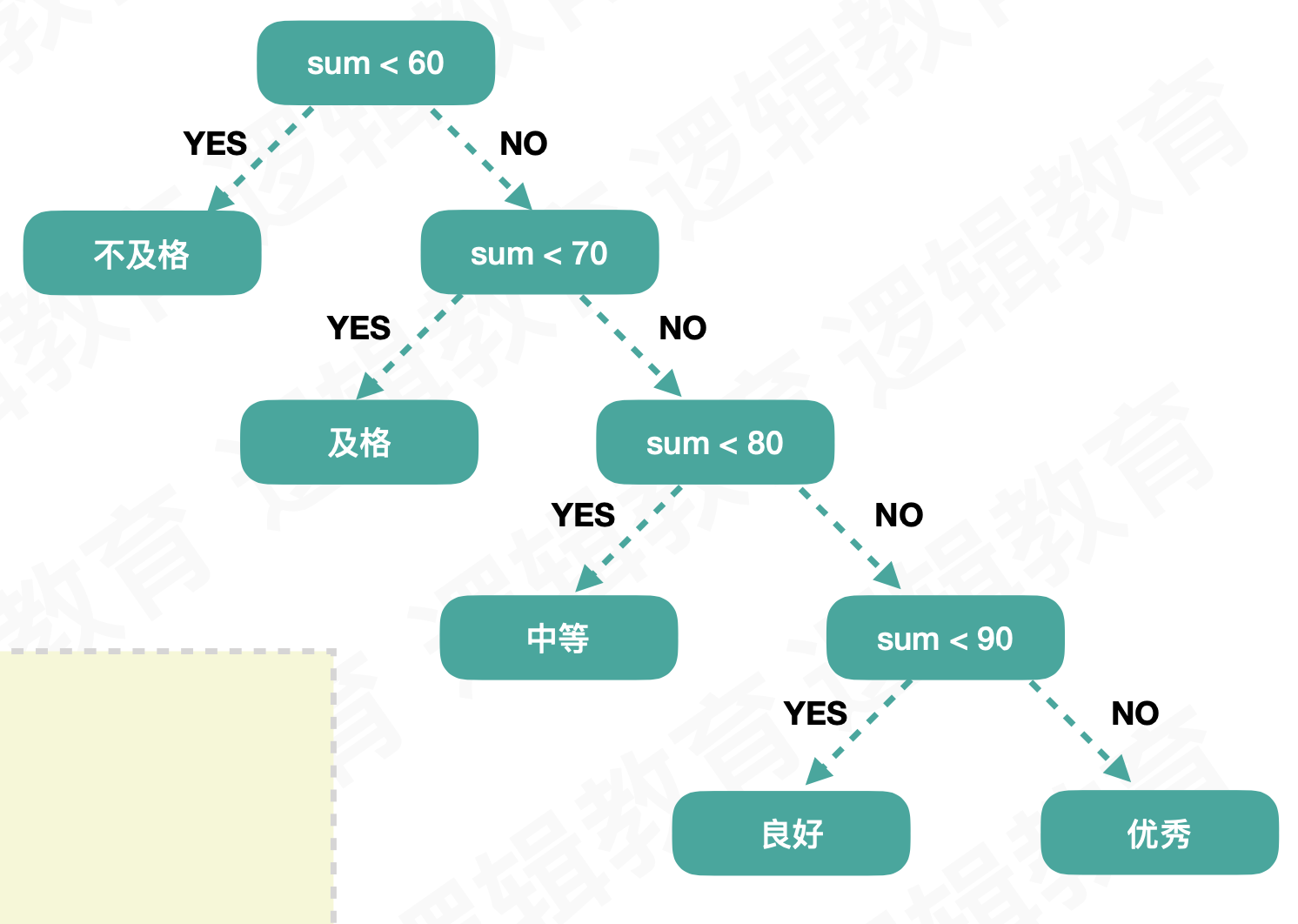
这样是判断貌似没什么问题,但是我们要思考一下学生的成绩分布如下:

成绩比重: 在70~89分之间占⽤用了了70% 但是都是需要经过3次判断才能得到正 确的结果. 那么如果数量集⾮常大时,这样的比较就会出现效率问题.
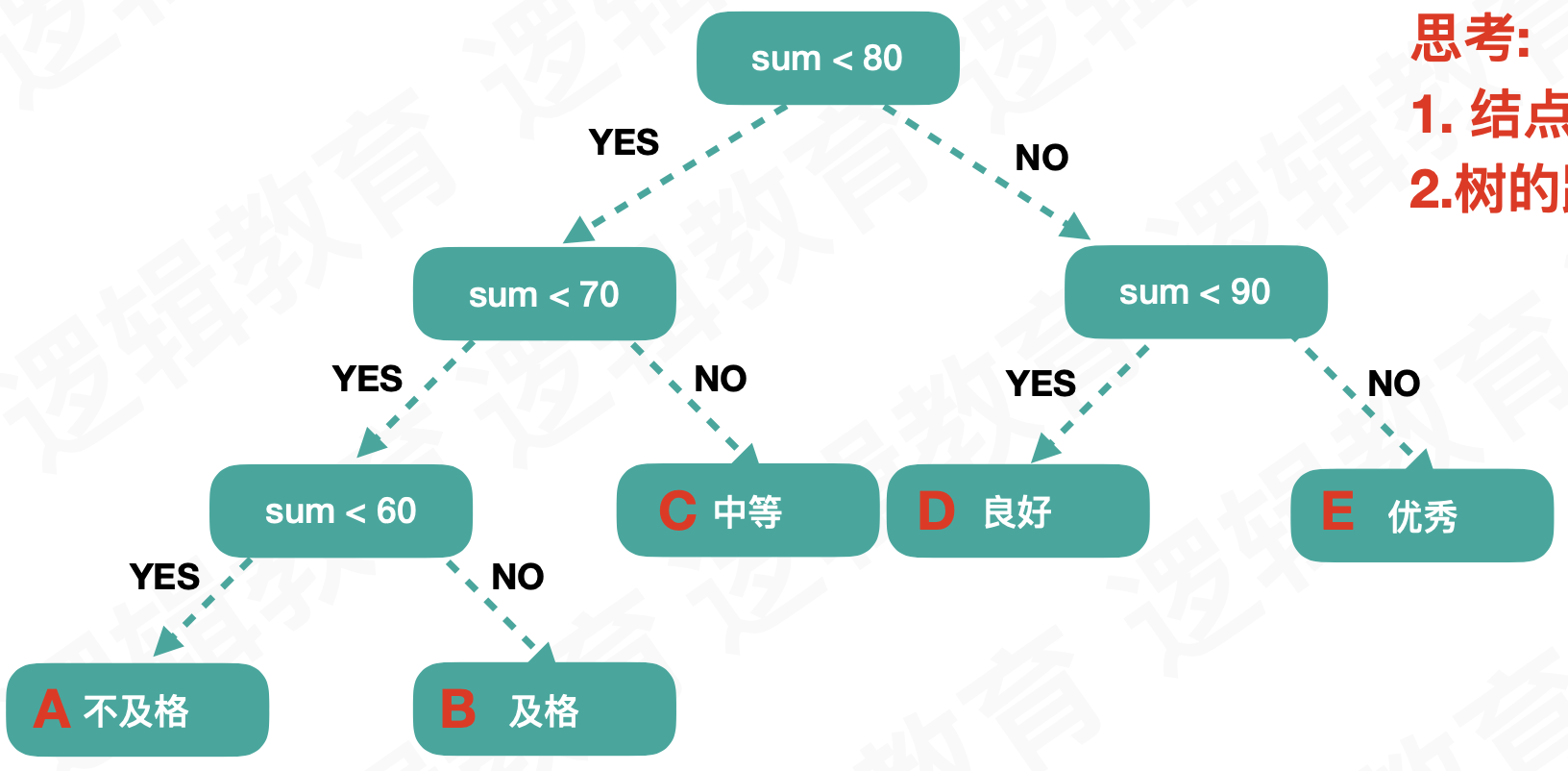
所以我们将判断的逻辑进行如上图一样的修改,是不是效率就会提高呢?
再继续哈夫曼思考之前,我们先补充一下几个概念:
路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径。
路径长度:在一条路径中,每经过一个结点,路径长度都要加1。例如在一棵树中,规定根结点所在层数为1层,那么从根结点到第 i 层结点的路径长度为 i - 1 。
结点的权:给每一个结点赋予一个新的数值,被称为这个结点的权。
结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积。
WPL:树的带权路径长度为树中所有叶子结点的带权路径长度之和
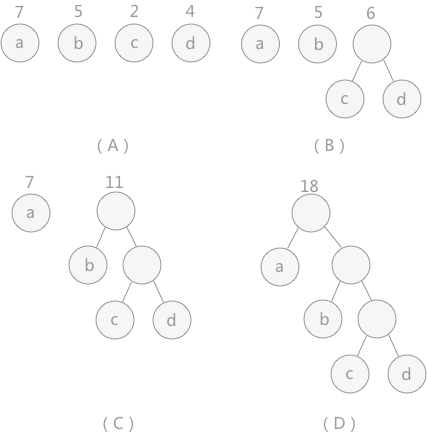
上面两种树的路径长度分别为:
1+1+2+2+3+3+4+4 = 20
1+2+3+3+2+1+2+2 = 16
WPL分别为:
1 * 5 + 2 * 15 + 3 *40 +4 * 30 + 4 * 10 = 315
5 * 3 + 15 * 3 + 40 * 2 + 30 * 2 +10 * 2 = 220
2.哈夫曼树
当用 n 个结点(都做叶子结点且都有各自的权值)试图构建一棵树时,如果构建的这棵树的带权路径长度最小,称这棵树为“最优二叉树”,有时也叫“赫夫曼树”或者“哈夫曼树”。
在构建哈弗曼树时,要使树的带权路径长度最小,只需要遵循一个原则,那就是:权重越大的结点离树根越近。
3.构建哈夫曼树
对于给定的有各自权值的 n 个结点,构建哈夫曼树有一个行之有效的办法:
1.在 n 个权值中选出两个最小的权值,对应的两个结点组成一个新的二叉树,且新二叉树的根结点的权值为左右孩子权值的和;
2.在原有的 n 个权值中删除那两个最小的权值,同时将新的权值加入到 n–2 个权值的行列中,以此类推;
3.重复 1 和 2 ,直到所以的结点构建成了一棵二叉树为止,这棵树就是哈夫曼树。
4.哈夫曼编码
哈夫曼编码就是在哈夫曼树的基础上构建的,这种编码方式最大的优点就是用最少的字符包含最多的信息内容。
根据发送信息的内容,通过统计文本中相同字符的个数作为每个字符的权值,建立哈夫曼树。对于树中的每一个子树,统一规定其左孩子标记为 0 ,右孩子标记为 1 。这样,用到哪个字符时,从哈夫曼树的根结点开始,依次写出经过结点的标记,最终得到的就是该结点的哈夫曼编码。
文本中字符出现的次数越多,在哈夫曼树中的体现就是越接近树根。编码的长度越短。
5.代码实现
const int MaxValue = 10000;//初始设定的权值最大值
const int MaxBit = 4;//初始设定的最大编码位数
const int MaxN = 10;//初始设定的最大结点个数
typedef struct HaffNode{
int weight;
int flag;
int parent;
int leftChild;
int rightChild;
}HaffNode;
typedef struct Code//存放哈夫曼编码的数据元素结构
{
int bit[MaxBit];//数组
int start; //编码的起始下标
int weight;//字符的权值
}Code;
//1.
//根据权重值,构建哈夫曼树;
//{2,4,5,7}
//n = 4;
void Haffman(int weight[],int n,HaffNode *haffTree){
int j,m1,m2,x1,x2;
//1.哈夫曼树初始化
//n个叶子结点. 2n-1
for(int i = 0; i < 2*n-1;i++){
if(i<n)
haffTree[i].weight = weight[i];
else
haffTree[i].weight = 0;
haffTree[i].parent = 0;
haffTree[i].flag = 0;
haffTree[i].leftChild = -1;
haffTree[i].rightChild = -1;
}
//2.构造哈夫曼树haffTree的n-1个非叶结点
for (int i = 0; i< n - 1; i++){
m1 = m2 = MaxValue;
x1 = x2 = 0;
//2,4,5,7
for (j = 0; j< n + i; j++)//循环找出所有权重中,最小的二个值--morgan
{
if (haffTree[j].weight < m1 && haffTree[j].flag == 0)
{
m2 = m1;
x2 = x1;
m1 = haffTree[j].weight;
x1 = j;
} else if(haffTree[j].weight<m2 && haffTree[j].flag == 0)
{
m2 = haffTree[j].weight;
x2 = j;
}
}
//3.将找出的两棵权值最小的子树合并为一棵子树
haffTree[x1].parent = n + i;
haffTree[x2].parent = n + i;
//将2个结点的flag 标记为1,表示已经加入到哈夫曼树中
haffTree[x1].flag = 1;
haffTree[x2].flag = 1;
//修改n+i结点的权值
haffTree[n + i].weight = haffTree[x1].weight + haffTree[x2].weight;
//修改n+i的左右孩子的值
haffTree[n + i].leftChild = x1;
haffTree[n + i].rightChild = x2;
}
}
/*
哈夫曼编码
由n个结点的哈夫曼树haffTree构造哈夫曼编码haffCode
//{2,4,5,7}
*/
void HaffmanCode(HaffNode haffTree[], int n, Code haffCode[])
{
//1.创建一个结点cd
Code *cd = (Code * )malloc(sizeof(Code));
int child, parent;
//2.求n个叶结点的哈夫曼编码
for (int i = 0; i<n; i++)
{
//从0开始计数
cd->start = 0;
//取得编码对应权值的字符
cd->weight = haffTree[i].weight;
//当叶子结点i 为孩子结点.
child = i;
//找到child 的双亲结点;
parent = haffTree[child].parent;
//由叶结点向上直到根结点
while (parent != 0)
{
if (haffTree[parent].leftChild == child)
cd->bit[cd->start] = 0;//左孩子结点编码0
else
cd->bit[cd->start] = 1;//右孩子结点编码1
//编码自增
cd->start++;
//当前双亲结点成为孩子结点
child = parent;
//找到双亲结点
parent = haffTree[child].parent;
}
int temp = 0;
for (int j = cd->start - 1; j >= 0; j--){
temp = cd->start-j-1;
haffCode[i].bit[temp] = cd->bit[j];
}
//把cd中的数据赋值到haffCode[i]中.
//保存好haffCode 的起始位以及权值;
haffCode[i].start = cd->start;
//保存编码对应的权值
haffCode[i].weight = cd->weight;
}
}