开场白
本文主要讲解一下排序方法:
- 冒泡
- 选择
- 插入
- 希尔
- 堆排序
以下代码中数组都是从下标1开始的,下标0用作哨兵;排序代码都是进行升序排列。
公共代码部分
展示部分公共代码,了解后会对后面代码的阅读减少一下障碍。
typedef struct {
int r[MAXSIZE + 1];
int length;
}SqList;
void swap(SqList *L, int i, int j) {
int temp = L->r[i];
L->r[i] = L->r[j];
L->r[j] = temp;
}
void print(SqList L) {
int i;
for (i = 1; i<L.length; i++) {
printf("%d,", L.r[i]);
}
printf("%d", L.r[i]);
printf("\n");
}
冒泡
冒泡排序应该是所有程序员最喜欢的排序方法,因为代码可读性非常高。
初级冒泡
//冒泡排序初级版本
void BubbleSort0(SqList *L) {
for (int i = 1; i< L->length; i++) {
for (int j = i+1; j<= L->length; j++) {
if (L->r[i] > L->r[j]) {
swap(L, i, j);
}
}
}
}
正宗的冒泡排序算法
我们平时所说的冒泡其实不是正宗的,真正的正宗冒泡其实是这样的
void BubbleSort(SqList *L) {
for (int i = 1; i< L->length; i++) {
for (int j = L->length - 1; j>=i; j--) {
if (L->r[j] > L->r[j+1]) {
swap(L, j, j+1);
}
}
}
}
内部for循环时从后往前的顺序。其实也没什么特别的,也很好理解。
冒泡排序优化
增加一个flag标志
void BubbleSort2(SqList *L) {
Status flag = TRUE;
for (int i = 1; i< L->length && flag; i++) {
flag = FALSE;
for (int j = L->length - 1; j>=i; j--) {
if (L->r[j] > L->r[j+1]) {
swap(L, j, j+1);
flag = TRUE;
}
}
}
}
其实就是可以提前跳出循环。
选择排序
void SelectSort(SqList *L) {
for (int i = 1; i < L->length; i++) {
int min = i;
for (int j = i+1; j <= L->length; j++) {
if (L->r[min] > L->r[j]) {
min = j;
}
}
if (i!=min) {
swap(L, i, min);
}
}
}
也比较简单,逻辑上和冒泡有点区别,先找到最小或者最大值,记录下来,内部循环接受后,与外部循环的i进行交换。
直接插入排序
void InsertSort(SqList *L) {
int temp = 0;
for (int i = 2; i<=L->length; i++) {
if (L->r[i]<L->r[i-1]) {
temp = L->r[i];
int j;
for (j=i-1; L->r[j]>temp; j--) {
L->r[j+1]=L->r[j];
}
L->r[j+1]=temp;
}
}
}
数组从前到后遍历中,当前元素小于它前面的元素(前面所有的元素已经排序完成),将当前元素出入到前面的已排完的顺序中。
希尔排序
void shellSort(SqList *L) {
int increment = L->length;
do {
increment = increment/3+1;
for (int i = increment+1; i<=L->length; i++) {
if (L->r[i] < L->r[i-increment]) {
L->r[0] = L->r[i];
int j;
for (j = i-increment; j > 0 && L->r[0]<L->r[j]; j-=increment) {
L->r[j+increment] = L->r[j];
}
L->r[j+increment] = L->r[0];
}
}
} while (increment > 1);
}
希尔排序的特点是修改了比较元素之间的步长距离,之前的排序都是临近的两个元素进行比较,而希尔排序是可以让编写者根据需求自行修改比较步长。这样有一个优点,根据步长的不同与业务需求,会得到不同的时间复杂度。
堆排序
什么叫堆
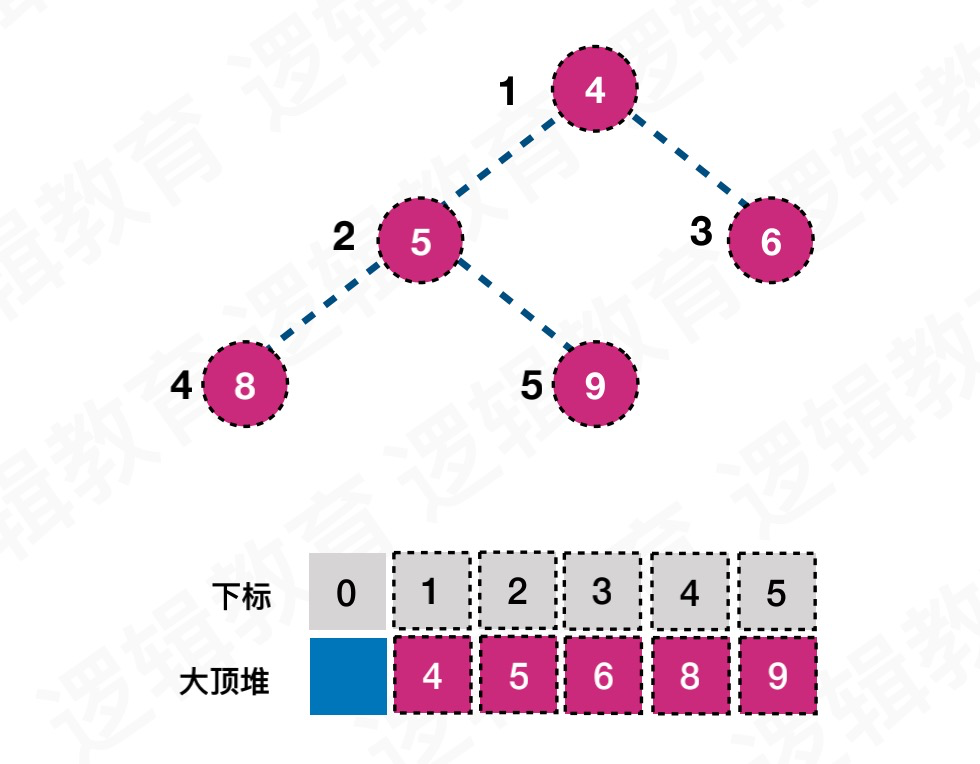
堆是具有下⾯性质的完全⼆叉树:每个结点的值都⼤于或等于其左右孩⼦结点的值,称为⼤顶堆;如图1;或者每个结点的值都⼩于等于其左右孩⼦的结点的值,称为⼩顶堆,如图2.
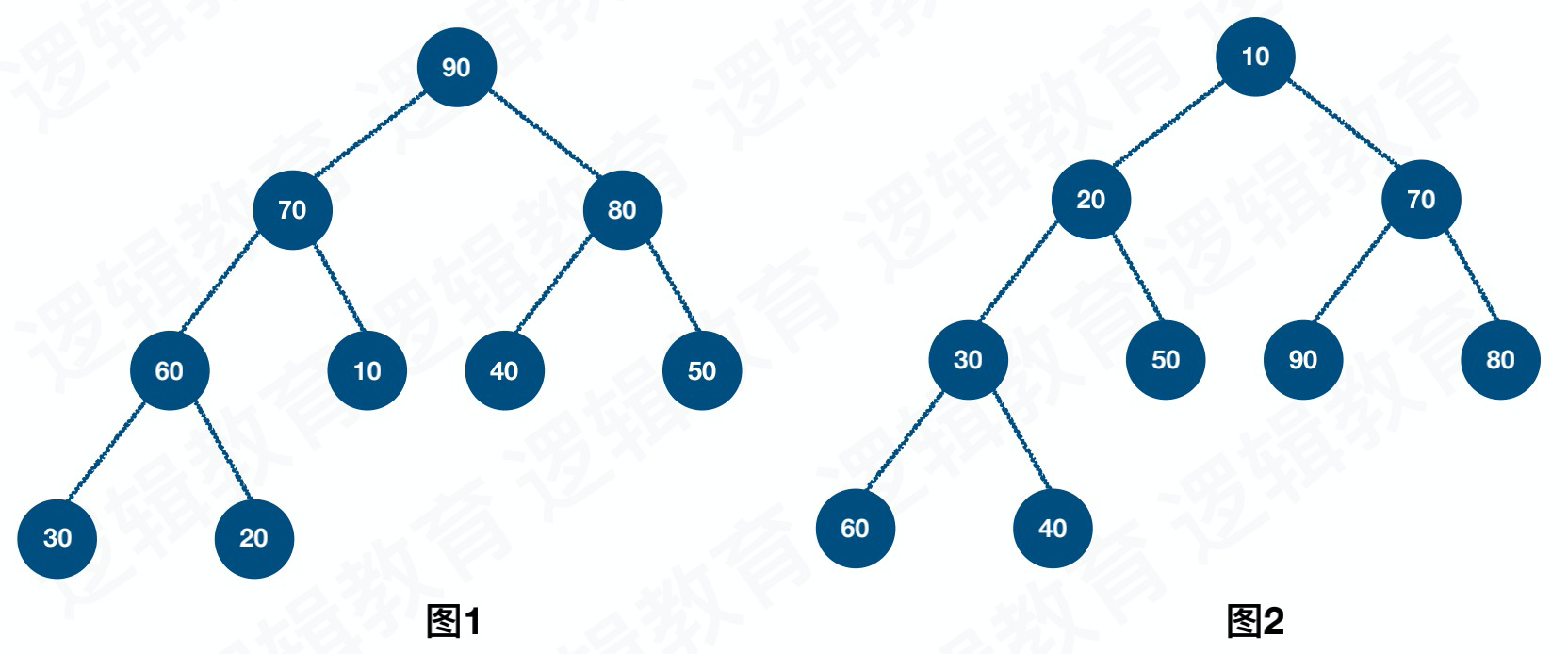
堆排序
堆排序(Heap Sort) 就是利⽤堆(假设我们选择⼤顶堆)进⾏排序的算法.它的基本思想:
- 将待排序的序列构成⼀个⼤顶堆,此时,整个序列的最⼤值就堆顶的根结点,将它移⾛(其实就是将其与堆数组的末尾元素交换, 此时末尾元素就是最⼤值);
- 然后将剩余的n-1个序列重新构成⼀个堆,这样就会得到n个元素的次⼤值,如此重复执⾏,就能得到⼀个有序序列了
示例
构造初始堆
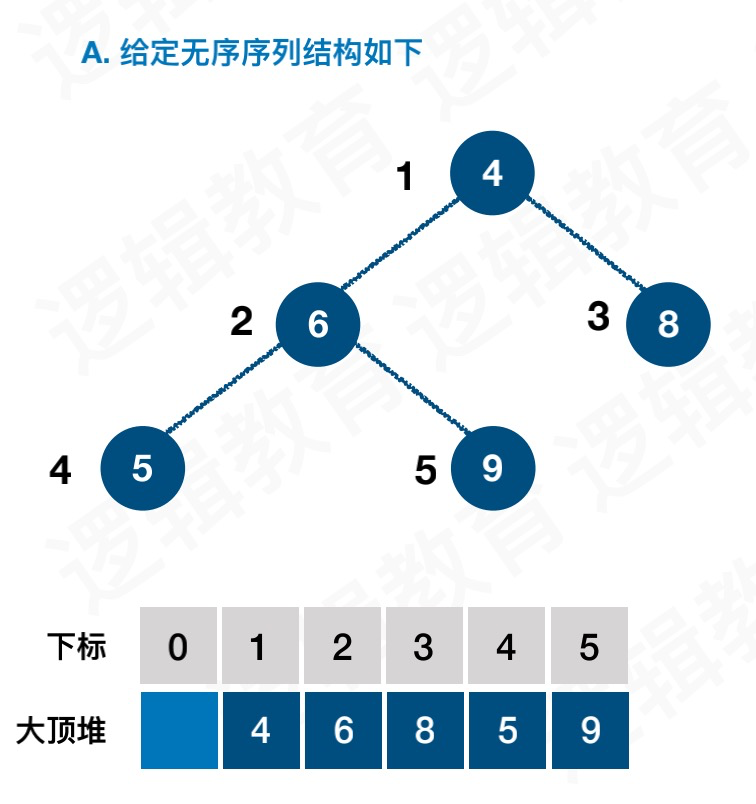
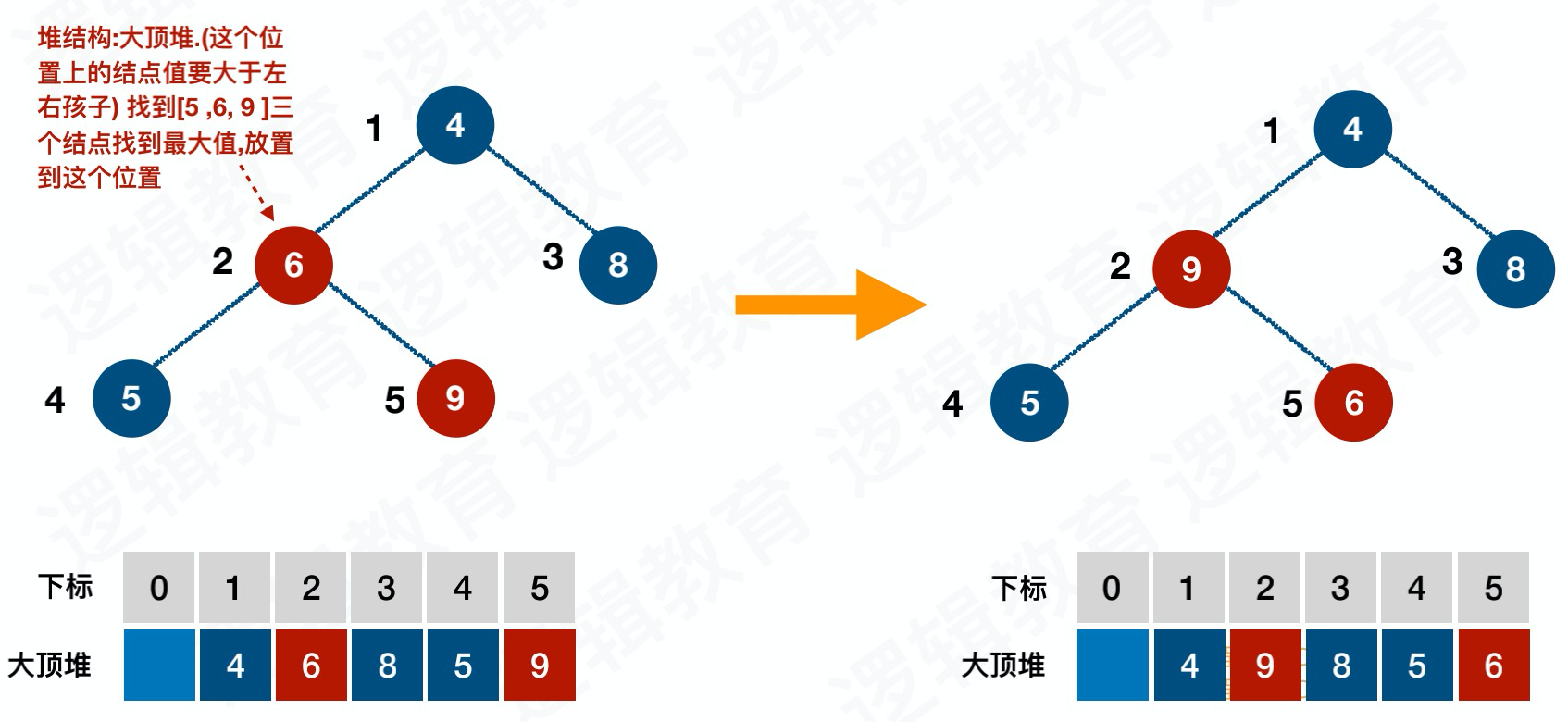
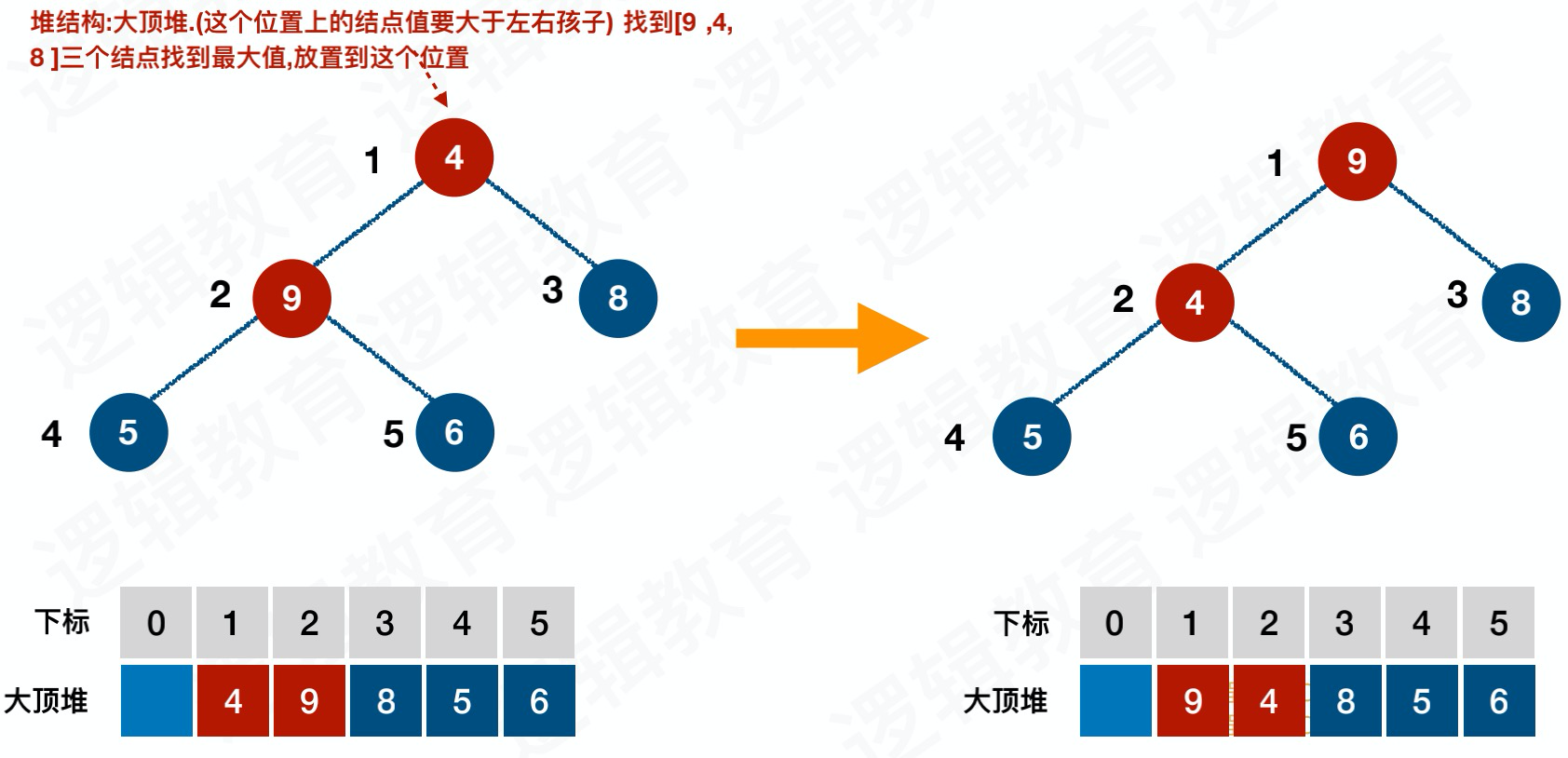
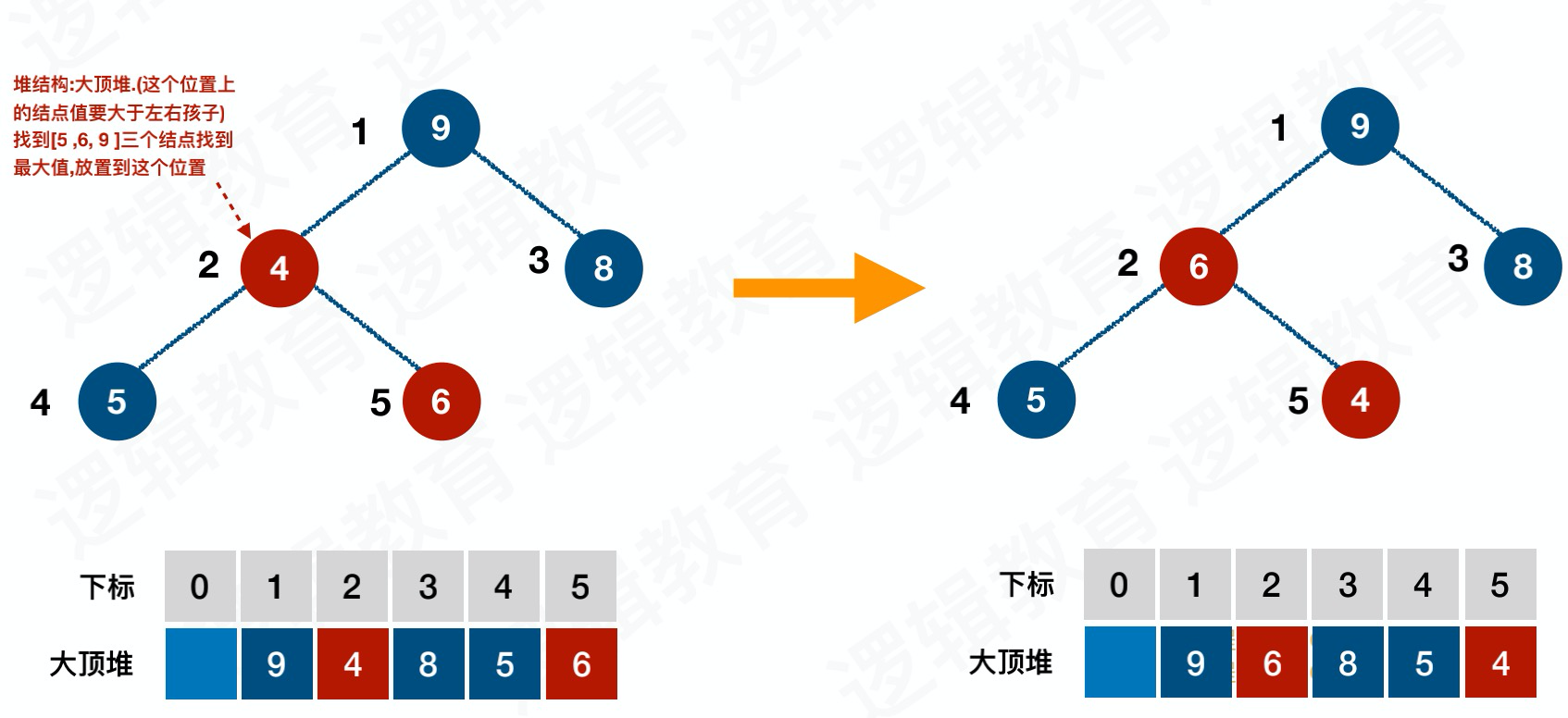
交换
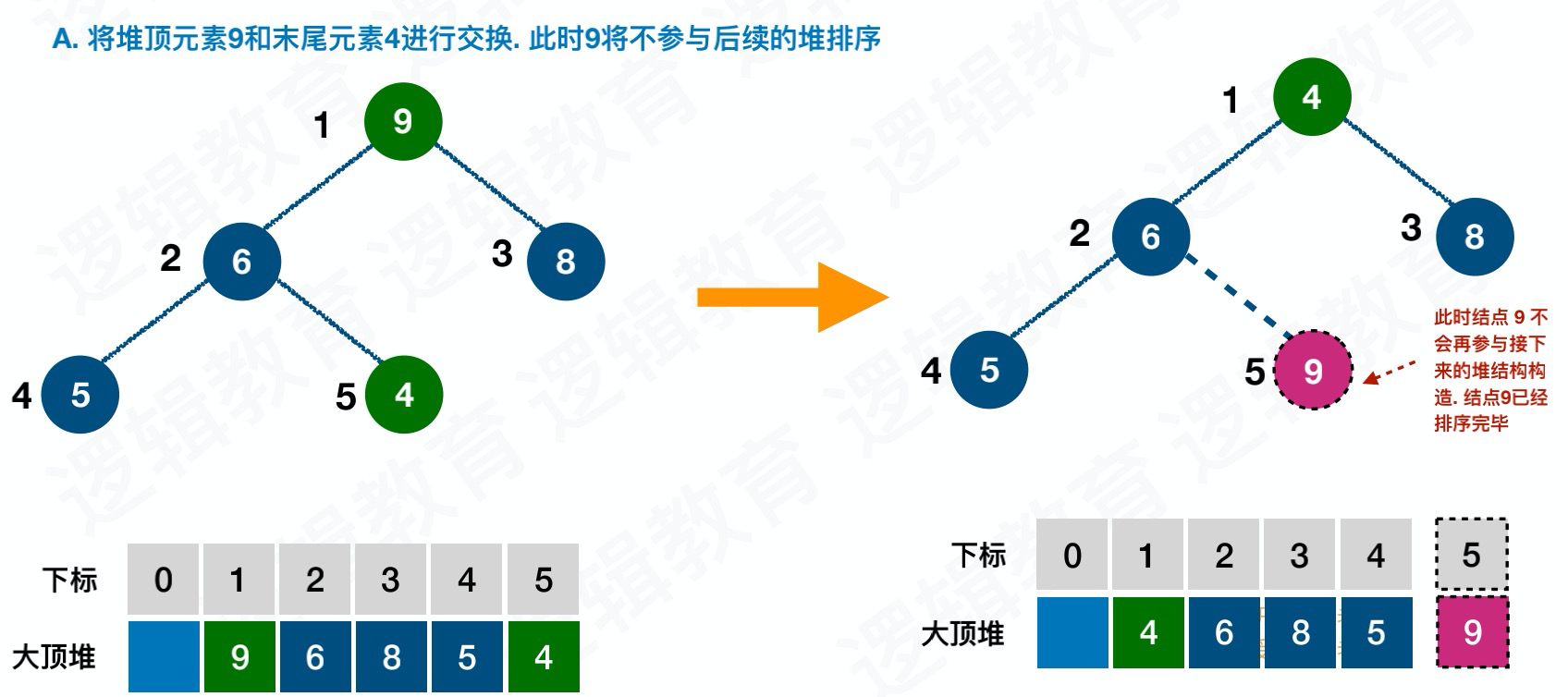
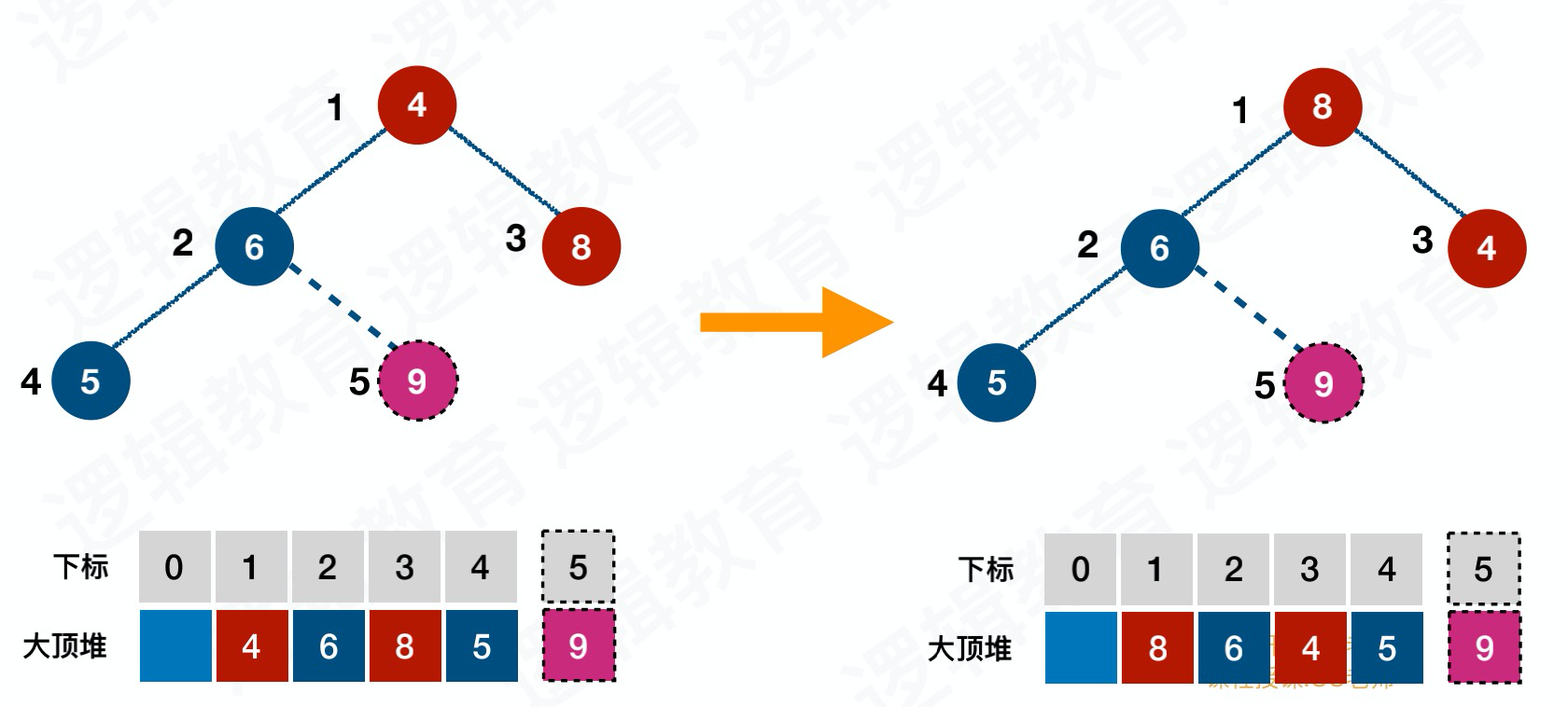
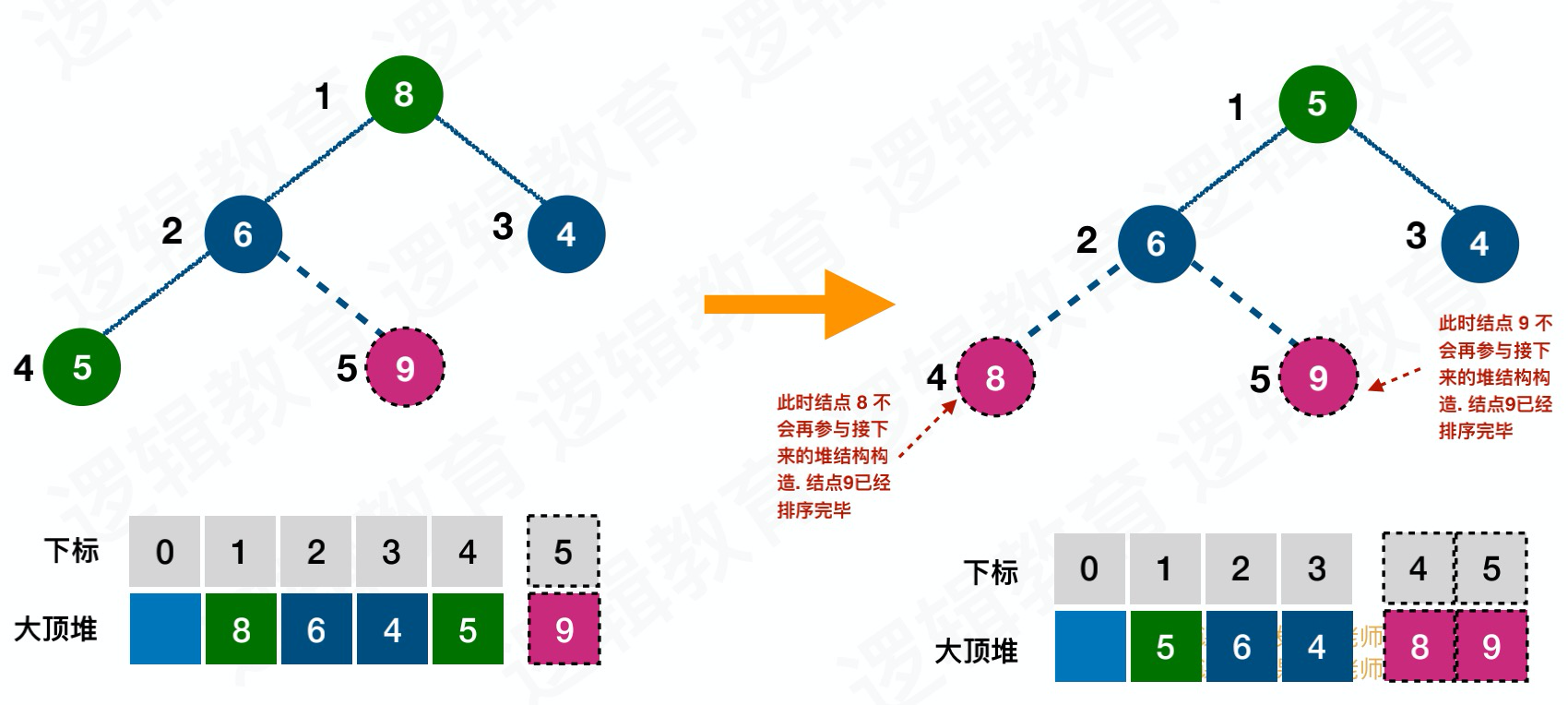
堆排序思路
- 将⽆序序列构建成⼀个堆,根据升序降序需求选择⼤顶堆或⼩顶堆
- 将堆顶元素与末尾元素交换,将最⼤元素“沉”到数组末端;
- 重新调整结构,使其满⾜堆定义,然后继续交换堆顶元素与当前末尾元素,反复执⾏调整+交换步骤,直到整个序列有序;
代码
//大顶堆调整函数
void HeapAdjust(SqList *L, int s, int m) {
int temp = L->r[s];
for (int j = 2*s; j <= m; j*=2) {
if (j < m && L->r[j] < L->r[j+1]) {
++j;
}
if (temp >= L->r[j]) {
break;
}
L->r[s] = L->r[j];
s = j;
}
L->r[s] = temp;
}
//堆排序
void HeapSort(SqList *L) {
for (int i=L->length/2; i>0; i--) {
HeapAdjust(L, i, L->length);
}
for (int i = L->length; i>1; i--) {
swap(L, 1, i);
HeapAdjust(L, 1, i-1);
}
}
以上排序算法的运行方法
#define N 9
int main(int argc, const char * argv[]) {
// insert code here...
printf("Hello, 排序算法\n");
int i;
int d[N]={9,1,5,8,3,7,4,6,2};
//int d[N]={9,8,7,6,5,4,3,2,1};
//int d[N]={50,10,90,30,70,40,80,60,20};
SqList l0,l1,l2,l3,l4,l5,l6,l7,l8,l9,l10;
for(i=0;i<N;i++)
l0.r[i+1]=d[i];
l0.length=N;
l1=l2=l3=l4=l5=l6=l7=l8=l9=l10=l0;
printf("排序前:\n");
print(l0);
printf("\n");
//1.初级冒泡排序
printf("初级冒泡排序:\n");
BubbleSort0(&l0);
print(l0);
printf("\n");
//2.冒泡排序
printf("冒泡排序:\n");
BubbleSort(&l1);
print(l1);
printf("\n");
//3.冒泡排序优化
printf("冒泡排序(优化):\n");
BubbleSort2(&l2);
print(l2);
printf("\n");
//4.选择排序
printf("选择排序:\n");
SelectSort(&l3);
print(l3);
printf("\n");
//5.直接插入排序
printf("直接插入排序:\n");
InsertSort(&l4);
print(l4);
printf("\n");
//6.希尔排序
printf("希尔排序:\n");
shellSort(&l5);
print(l5);
printf("\n");
//7.堆排序
//注意:执行对排序时更换一下数据源. 这里我为什么要这组数据,原因是为了与下标个位数字讲解时进行区分;因为在这个算法讲解过程,出现了很多下标的相关计算.
/* int d[N]={50,10,90,30,70,40,80,60,20}; */
printf("堆排序:\n");
HeapSort(&l6);
print(l6);
printf("\n");
printf("\n");
return 0;
}
