散列技术
散列技术是记录的存储位置和它的关键字之间建⽴⼀个确定的对应关系f,使得每个关键字key对应⼀个存储位置f(key). 查找时,根据这个对应关系找到给定值 key的映射f(key). 若查找集合中存在这个记录,则必定在f(key)的位置上.
实现方式
总体的实现方法都是对key进行一定的规则转换,并且尽量避免结果冲突。
1.直接定址法
f(key) = a * key + b (a,b为常数); 例如:
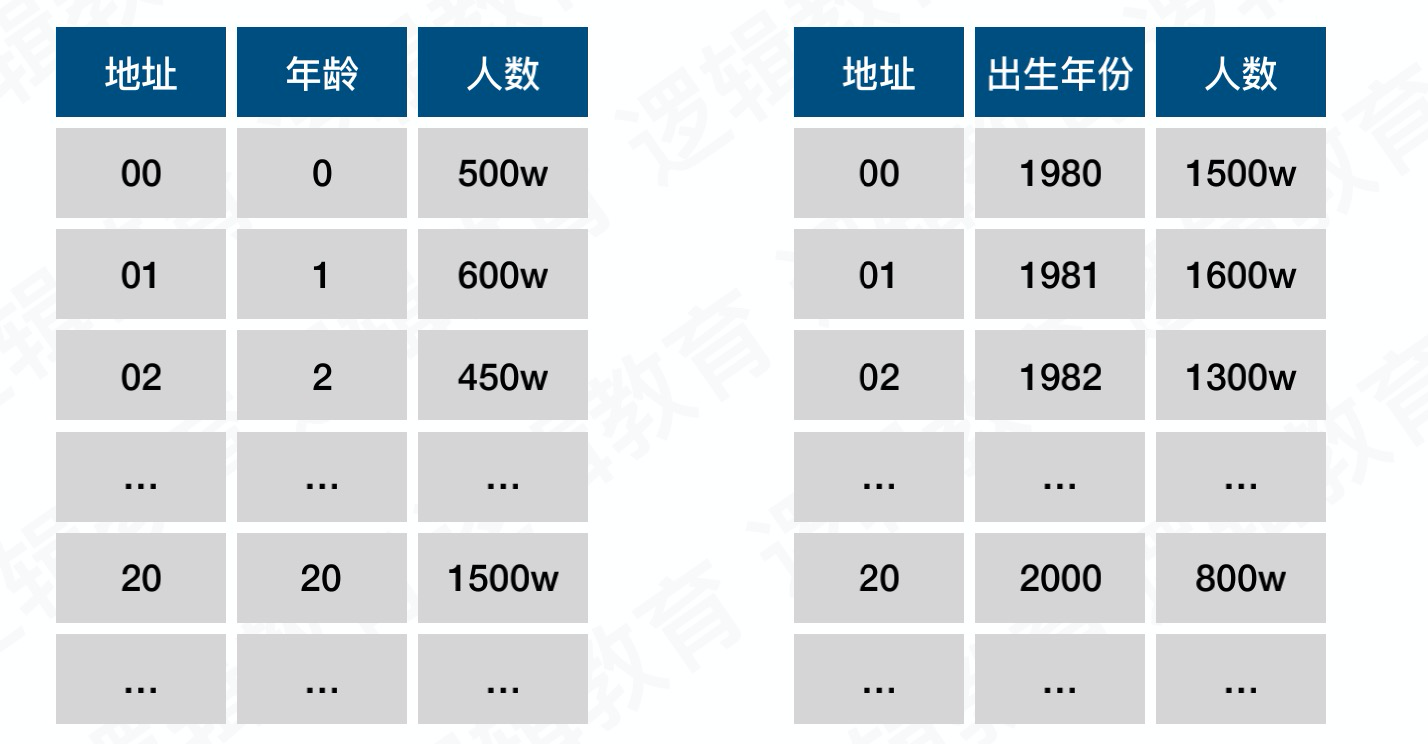
2.数字分析法
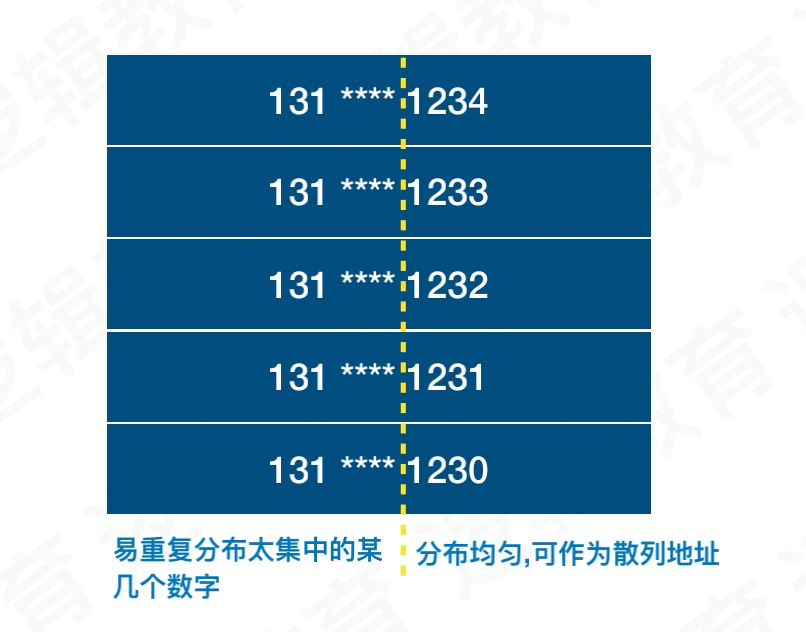
3.平方取中法
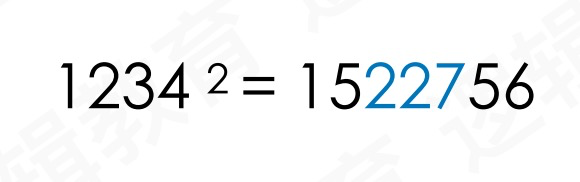
4.折叠法
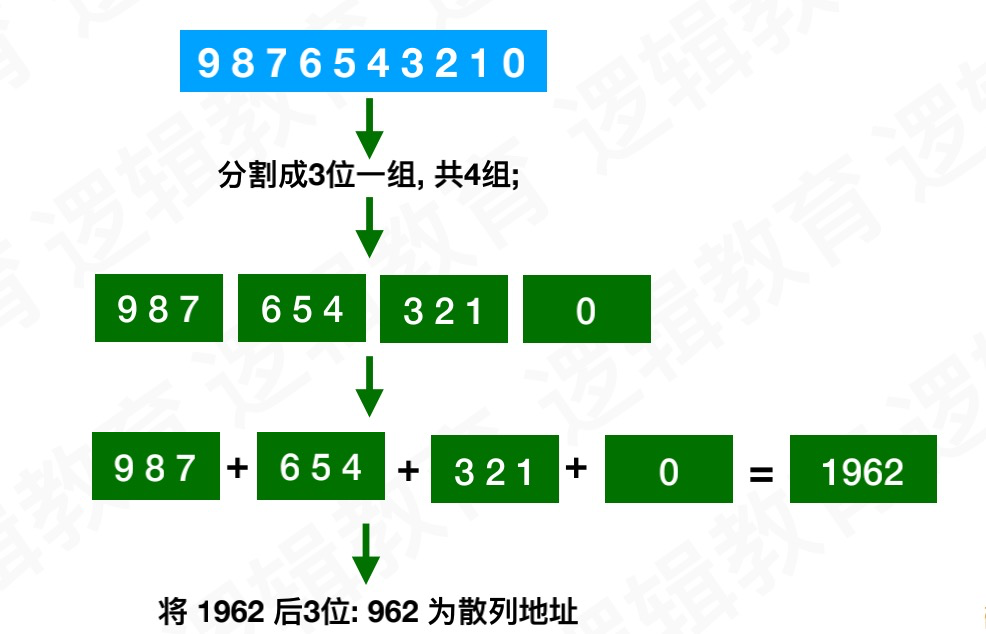
5.除留余数法
f(key) = key mod p (p <= m)
处理冲突
1.开放地址法
开放定址法就是⼀旦发⽣了冲突,就去寻找下⼀个空的散列地址.只有散列表⾜够⼤,空的散列地址总能找到,并将记录存⼊.
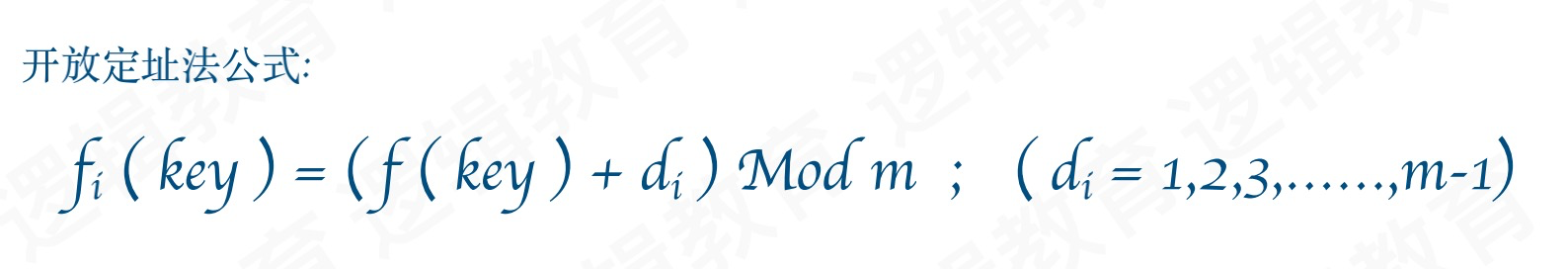
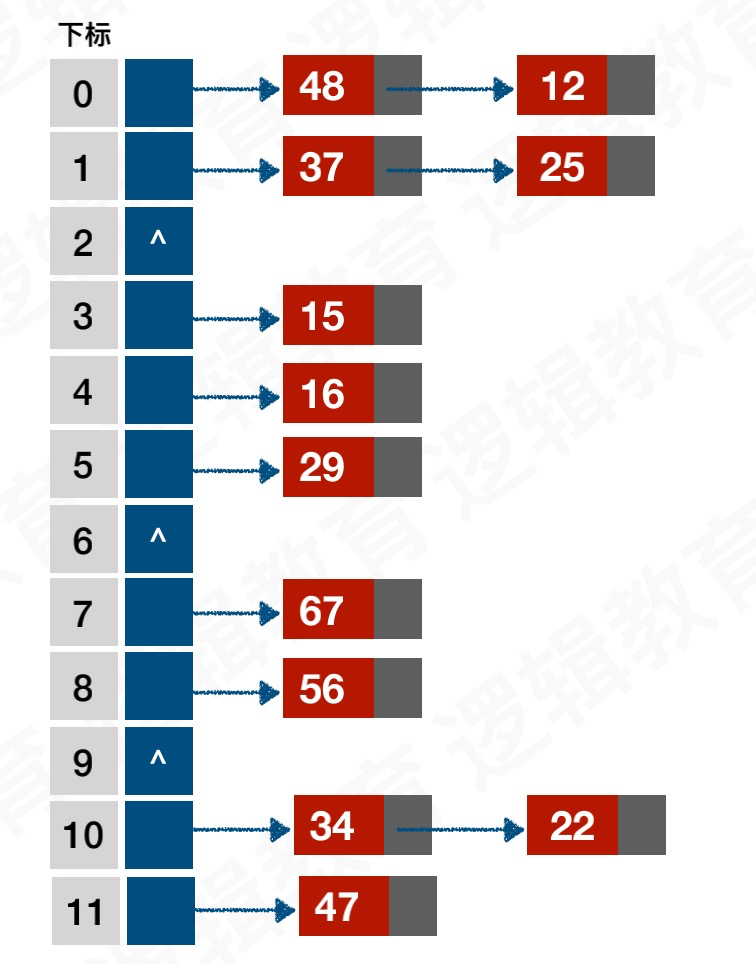
关键字集合 { 12,67,56,16,25,37,22,29,15,47,48,34 } 表⻓为12, 我们⽤散列函数f ( key ) = key mod 12;
- 计算{12,67,56,16,25 } 是没有发⽣散列冲突的,也没有出现同义词;

- key=37,f(37)=1,与25冲突;使用开放地址公式f(37)=(f(37)+1)mod 12 = 2;下标2位置上是空,存储下来

- 存储22,29,15,47 按照f(key) = key mod 12,没有出现冲突,即可直接存储进去.

- f(48) = 48 mod 12 = 0;此时0的位置上已经存储了数据12.那么12和48就是同义词了。使用开放地址法f(48)=(f(48)+2)mod 12=1;与25冲突。继续往下使用开放地址发f(48)=(f(48)+6)mod 12=6时。此时6位置上没有数据,则48存储到6的位置上。

- f(34)=10,但是的位置是22,冲突了。但此时10以后的位置已经没有空闲的控件了。10的前面还有。通过开放定制公式,一直取模求余,是可以得到结果的,但是效率太低。我们之前使用的开放定址法解决冲突被称为线性探测法,还有一种解决冲突的方法叫做二次探索发
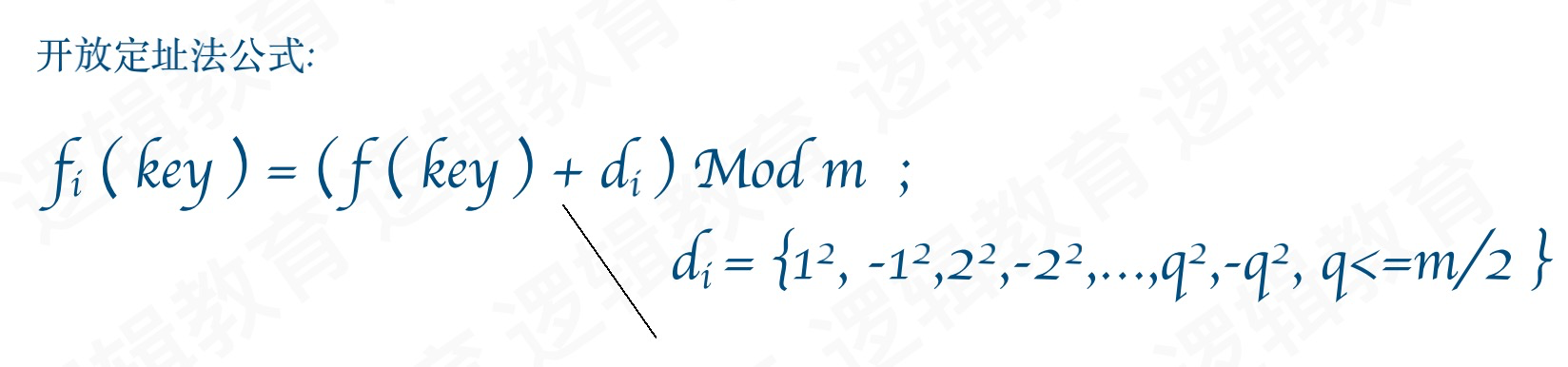

2.再散列函数法
对于散列表来说, 我们事先准备多个散列函数:

3.链地址法
将所有的关键字为同义词的记录存储在⼀个单链表中,我们称为这种同义词⼦表. 在散列表中只存储所有同义词⼦表的头指针(头地址).
4.公共溢出法
这种方式不推荐,因为对空间消耗很大
代码
#include <stdio.h>
#include "stdlib.h"
#define OK 1
#define ERROR 0
#define SUCCESS 1
#define UNSUCCESS 0
#define HASHSIZE 12
#define NULLKEY -32768
typedef int Status;
//散列表结构体
typedef struct Hash{
int *elem;
int count;
}HashTable;
//全局变量的散列表
int m = 0;
//初始化散列表
Status InitHashTable(HashTable *H) {
m = HASHSIZE;
H->count = m;
H->elem = (int*)malloc(sizeof(int) *m);
for (int i = 0; i< m; i++) {
H->elem[i]=NULLKEY;
}
return OK;
}
//散列函数
int Hash(int key) {
return key % m;//除留余数法
}
//插入函数
void InsertHash(HashTable *H, int key) {
int addr = Hash(key);
while (H->elem[addr] != NULLKEY) {
addr = (addr + 1) % m;//开放定址法
}
H->elem[addr] = key;
}
//查找函数
Status SearchHash(HashTable H, int key, int *addr) {
*addr = Hash(key);
while (H.elem[*addr] != key) {
*addr = (*addr + 1) %m;
//当前的位置为初始值 或者 回到了起点,说明key不存在
if (H.elem[*addr] == NULLKEY || *addr == Hash(key)) {
return UNSUCCESS;
}
}
return SUCCESS;
}
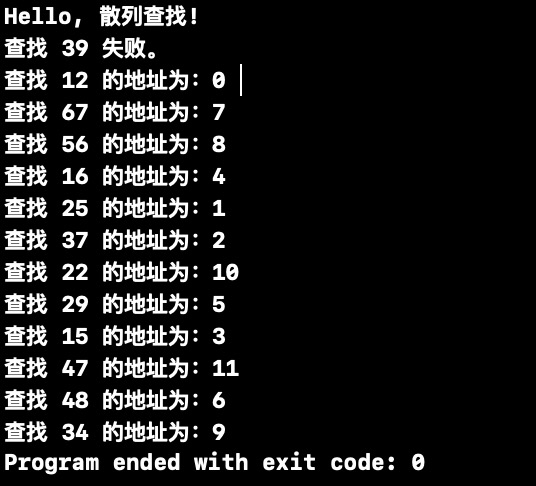
运行
int main(int argc, const char * argv[]) {
// insert code here...
printf("Hello, 散列查找!\n");
int arr[HASHSIZE]={12,67,56,16,25,37,22,29,15,47,48,34};
int i,p,key,result;
HashTable H;
//1.初始化散列表
InitHashTable(&H);
//2.向散列表中插入数据
for(i=0;i<m;i++)
InsertHash(&H,arr[i]);
//3.在散列表查找key=39
key=39;
result=SearchHash(H,key,&p);
if (result)
printf("查找 %d 的地址为:%d \n",key,p);
else
printf("查找 %d 失败。\n",key);
//4.将数组中的key,打印出所有在散列表的存储地址
for(i=0;i<m;i++)
{
key=arr[i];
SearchHash(H,key,&p);
printf("查找 %d 的地址为:%d \n",key,p);
}
return 0;
}