数据结构与算法-Day18-排序排序可以说是最基本的算法了。直接开始每次循环找出当前序列中最小的元素，依次放在数组的顶

排序可以说是最基本的算法了。直接开始
辅助函数：

//交换数组中两个元素的个数
void swap(int *array, int i, int j) {
    int temp = array[i];
    array[i] = array[j];
    array[j] = temp;
}
//打印数组
void printArray(int *array, int length) {
    for(int i = 0; i < length; i++) {
        printf("%2d", array[i]);
    }
    printf("\n");
}

交换排序

每次循环找出当前序列中最小的元素，依次放在数组的顶部。

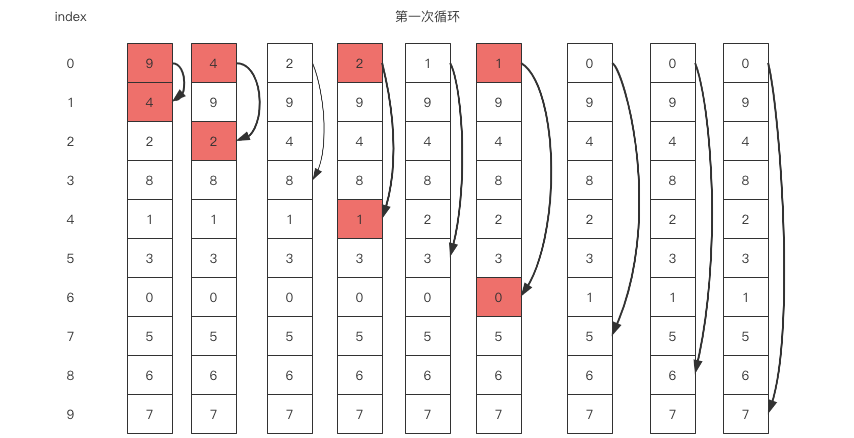
void switchSort(int *array, int length) {
    int i,j;
    for(i = 0; i < length; i++) {
        for(j = i+1; j < length; j++) {
            if(array[j] < array[i]) {
                swap(array, i, j);
            }
        }
    }
    printArray(array, length);
}

时间复杂度O(n²)，是不稳定的排序。

冒泡排序

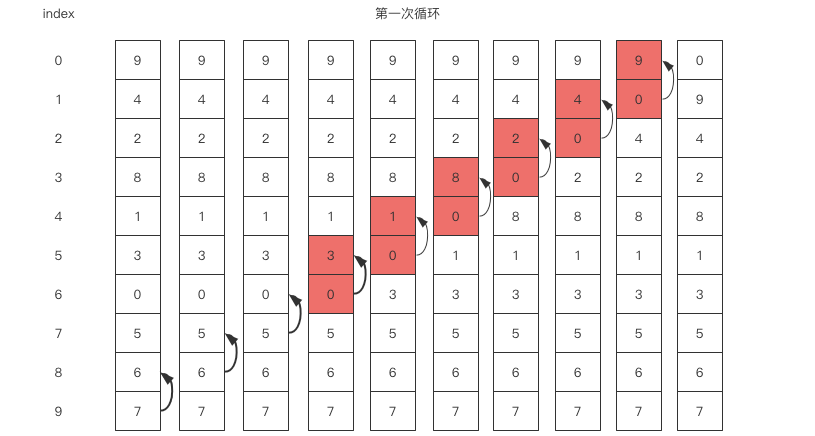
void bubbleSort_1(int *array, int length) {
    int i,j;
    for(i = 0; i < length; i++) {
        //从length-1开始，依次对比相邻的两个元素，小的元素和冒泡一样，进行上移。
        for(j = length-1; j > i; j--) {
            if(array[j] < array[j-1]) {
                swap(array, j, i);
            }
        }
    }
}

时间复杂度O(n²)，是稳定的排序。

选择排序

void selectionSort(int *array, int length) {
    int i,j;
    int min ;
    for(i = 0; i < length-1; i++) {
        min = i;
        //遍历i后面的元素，找到最小的元素与i进行交换
        for(j = i+1; j < length; j++) {
            if(array[j] < array[min]) {
                min = j;
            }
        }
        if(min != i) {
            swap(array, i, min);
        }
    }
    printArray(array, length);
}

时间复杂度O(n²)，是不稳定的排序。

插入排序

void insertSort(int *array, int length) {
    int i,j;
    int temp;
    int count = 0;
    for(i = 1; i < length; i++) {
        if(array[i-1] > array[i]) {
            temp = array[i];
            for(j = i - 1; j>=0 && array[j] > temp; j--) {
                count++;
                array[j+1] = array[j];
            }
            array[j+1] = temp;
        }
    }
    printf("count = %d", count);
    printArray(array, length);
}

时间复杂度O(n²)，是稳定的排序。

希尔排序

和选择排序相比，希尔排序把数组以特定的间隔分为几个小型的数组，对这些小型的数组进行插入排序。

void shellSort(int *array, int length) {
    int i,j;
    int increment = length/3;
    int temp;
    while(increment >= 1) {
        for(i = increment; i < length; i++) {
            if(array[i] < array[i-increment]) {
                temp = array[i];
                for(j = i-increment; j >= 0 && array[j] > temp; j-=increment) {
                    array[j+increment] = array[j];
                }
                array[j+increment] = temp;
            }
        }
        increment = increment/3;
    }
    printArray(array, length);
}

时间复杂度O(n²)，是不稳定的排序

堆排序

堆的概念
在含有 n 个元素的序列中，如果序列中的元素满足下面其中一种关系时，此序列可以称之为堆。

k[i] ≤ k[2i] 且 ki ≤ k[2i+1]（在 n 个记录的范围内，第 i 个关键字的值小于第 2i 个关键字，同时也小于第 2i+1 个关键字），通常称为小顶堆。
k[i]≥ k[2i] 且 ki ≥ k[2i+1]（在 n 个记录的范围内，第 i 个关键字的值大于第 2i 个关键字，同时也大于第 2i+1 个关键字），通常称为大顶堆。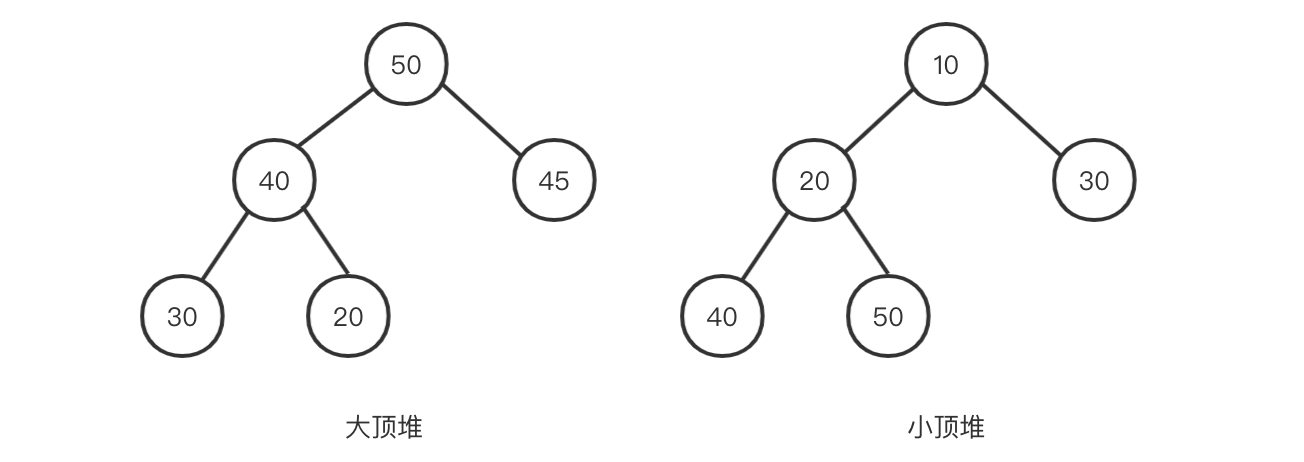
堆类似于完全二叉树的定义。 堆排序思路

将当前序列构建成为一个大顶堆（小顶堆）。
将堆顶元素和堆尾元素进行交换并输入，将n-1个元素的堆重新构建成为大顶堆（小顶堆），重复步骤1。

我们先来研究一下第二步，将堆顶元素输出之后，如何重新构建大顶堆。

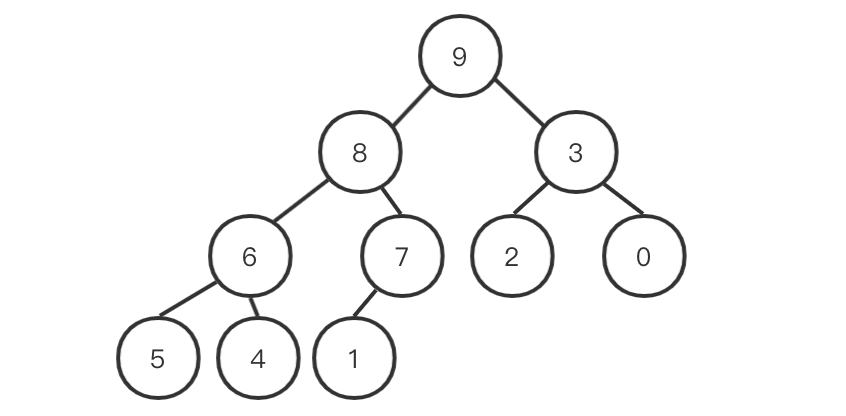
上图是一个大顶堆，顶点9是最大元素，我们将9和1进行交换。

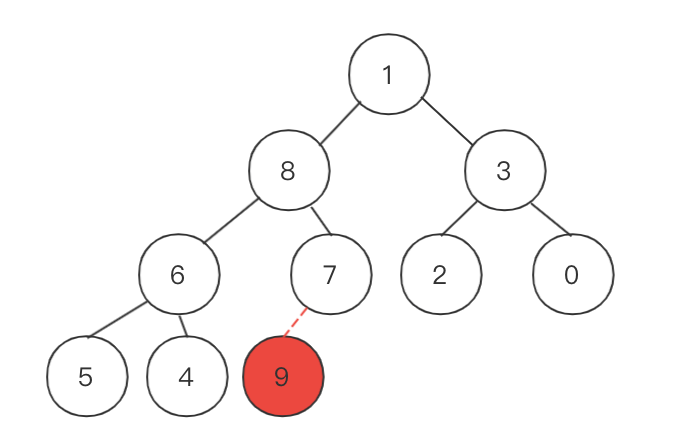
除了1之外，其他的都满足大顶堆。顶点9我们认为已经排好序了，可以先忽略。
因为其他的顶点都满足大顶堆，因此我们只需要确认1和它的两个子节点8、3当中，谁是最大的值并且进行交换。交换结束之后可以确保当前的堆顶为序列中最大元素。如下所示：

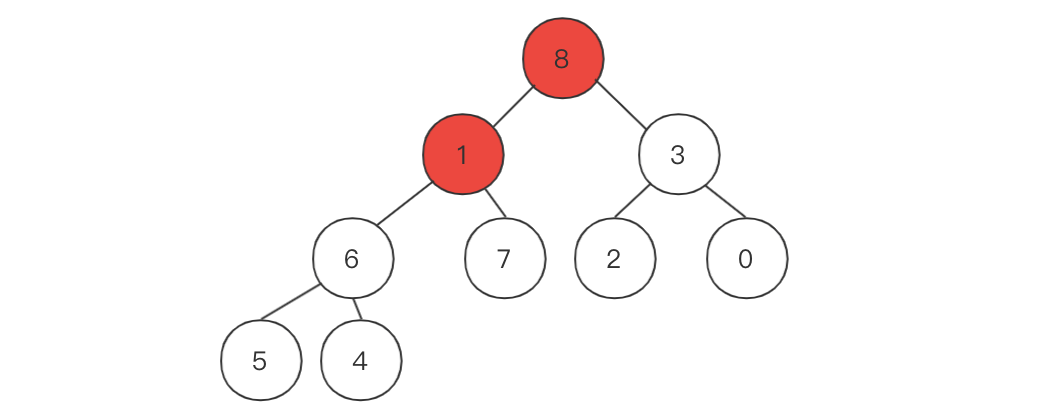
1<8，因此交换1和8。
此时我们发现8的位置正确了，但是1的位置还不正确。这时候就继续对比和替换，直到1放在合适的位置上。

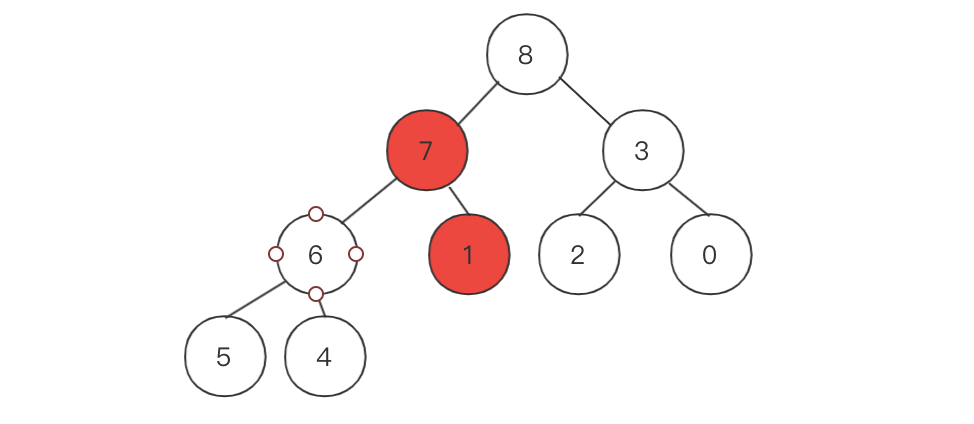
此时，交换1、9之后新的大顶堆调整完毕。

接下来看如何把无序的数据构建成一个大顶堆呢？

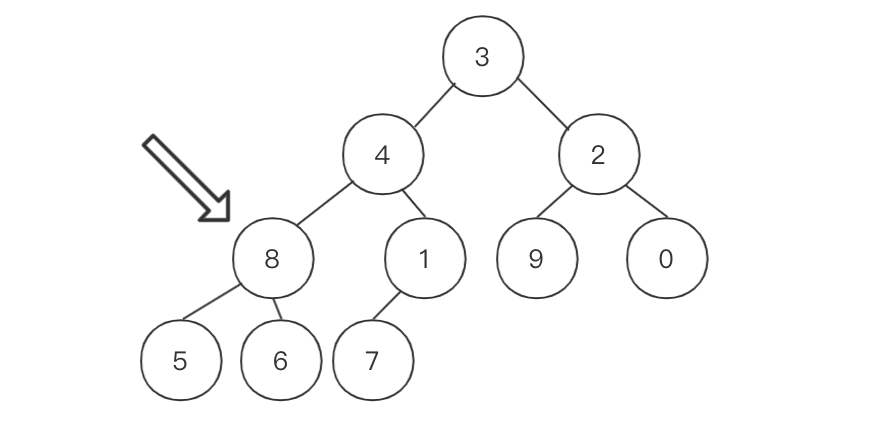
对于原始序列来说，因为叶子结点没有子结点，我们可以认为它已经是一个大顶堆。那么我们从最后一个有叶子结点的结点开始，即上图中的8，依次逆序来调整当前结点合计子结点，就可以得到一个构建好的大顶堆。代码

//从结点p开始调整它的子结点使其成为大顶堆
void heapAdjust(int *array, int p, int lenght) {
    int temp = array[p];
    for(int i = 2*p+1; i < lenght; i = i*2+1) {
        //找到子结点中较大的一个
        if(i+1 < lenght && array[i] < array[i+1]) {
            i++;
        }
        //如果比子结点中较大的还大，则不需要调整
        if(temp >= array[i]) {
            break;
        }else {
            //子结点较大的结点上移为父结点，继续遍历。
            if(temp < array[i]) {
                array[p] = array[i];
                p = i;
            }
        }
    }
    array[p] = temp;
    
}
//堆排序
void heapSort(int *array, int length) {
    int i;
    for(i = length/2; i>=0; i--) {
        heapAdjust(array, i, length);
    }
    for(i = 0; i < length-1; i++) {
        swap(array, 0, length-1-i);
        heapAdjust(array, 0, length-1-i);
    }
    printArray(array, length);
}

时间复杂度O(nlgn)，是不稳定的排序