方法一,利用视锥体平面
-
在介绍这种方法之前,需要先了解一下平面方程:有点法式,截距式,一般式。详细教程
-
再然后需要了解一下某个点到平面的距离:推导过程
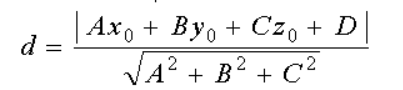
-
当法向量为单位向量时,分母可以去掉,并且这里加绝对值是为了保证值为正,视情况判断是否需要加绝对值。
-
GeometryUtility.CalculateFrustumPlanes(Camera.main),该方法返回摄像机的6个裁剪平面。顺序为[0] = Left, [1] = Right, [2] = Down, [3] = Up, [4] = Near, [5] = Far。所以可以通过如下方式判断一个点是否再视锥体中。
-
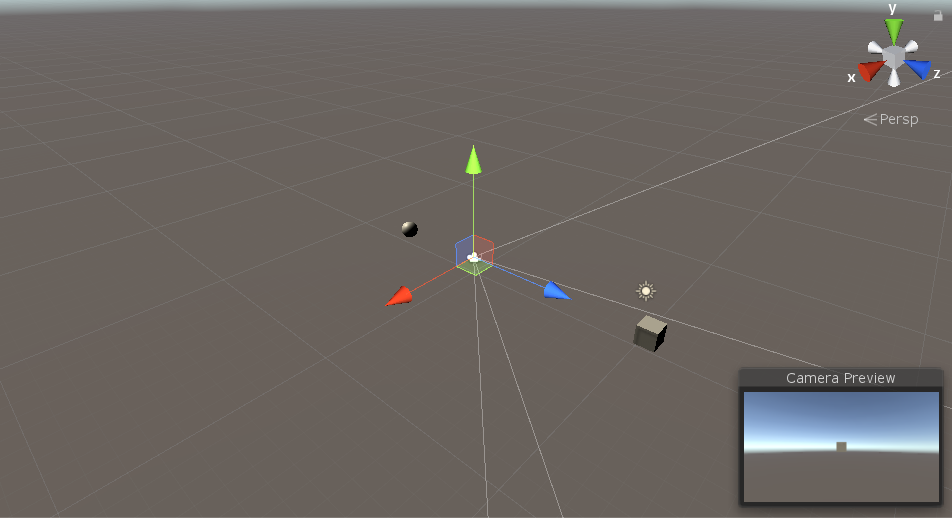
首先创建如下的场景,球赋给outView,正方体赋给inView。
public class Test : MonoBehaviour
{
public Transform inView;
public Transform outView;
// Start is called before the first frame update
void Start()
{
Debug.Log(TestInCamreaView1(inView.position));
Debug.Log(TestInCamreaView1(outView.position));
}
public bool TestInCamreaView1(Vector3 pos)
{
Vector4[] planeInfo = new Vector4[6];
var planes = GeometryUtility.CalculateFrustumPlanes(Camera.main);
for (int i = 0; i < 6; i++)
{
Plane p = planes[i];
//此时的normal已经为归一化的单位向量
planeInfo[i] = new Vector4(p.normal.x,p.normal.y,p.normal.z,p.distance);
}
for (int i = 0; i < 6; i++)
{
var normal = new Vector3(planeInfo[i].x,planeInfo[i].y,planeInfo[i].z);
var dist = planeInfo[i].w;
//根据点到平面距离的公式,此处不加绝对值,若点在视锥体外,距离为负数
if (Vector3.Dot(normal,pos) + dist <= 0)
{
return false;
}
}
return true;
}
// Update is called once per frame
void Update()
{
}
}
- 运行结果:
- 该方法遗憾的是每帧都会产生gc。
方法二,计算每个面的法向量,然后计算从摄像机位置到物体位置的向量与平面的法线点积是否为正,取交集即可判断是否在视锥体内。
- 以左右面为例
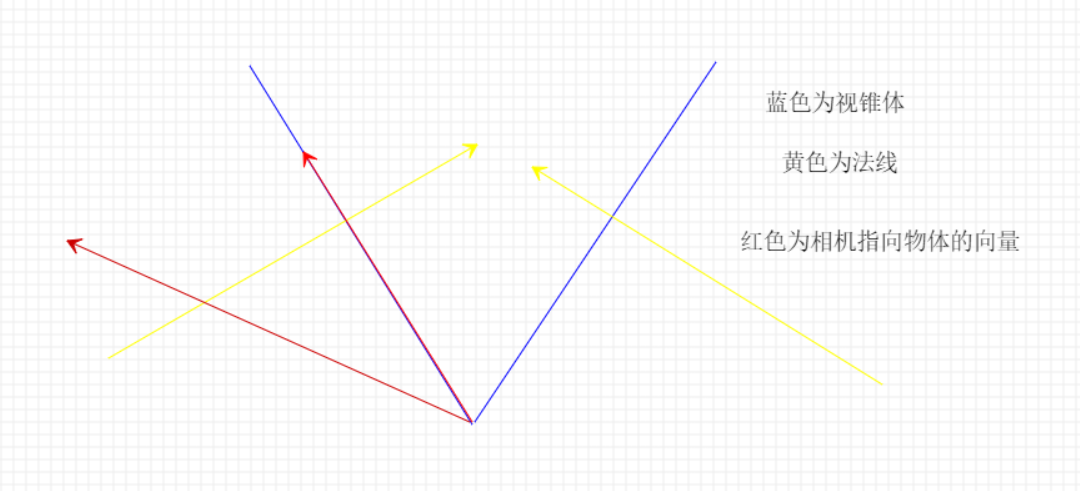
- 当相机指向物体的向量与视锥体面重合时,正好与视锥体面垂直,此时二者点积为0;若在视锥体外,二者夹角为钝角,点积小于0
public class Test : MonoBehaviour
{
public Transform inView;
public Transform outView;
// Start is called before the first frame update
void Start()
{
Debug.Log(TestCameraView2(inView.position));
Debug.Log(TestCameraView2(outView.position));
}
public bool TestInCamreaView1(Vector3 pos)
{
Vector4[] planeInfo = new Vector4[6];
var planes = GeometryUtility.CalculateFrustumPlanes(Camera.main);
for (int i = 0; i < 6; i++)
{
Plane p = planes[i];
//此时的normal已经为归一化的单位向量
planeInfo[i] = new Vector4(p.normal.x,p.normal.y,p.normal.z,p.distance);
}
for (int i = 0; i < 6; i++)
{
var normal = new Vector3(planeInfo[i].x,planeInfo[i].y,planeInfo[i].z);
var dist = planeInfo[i].w;
//根据点到平面距离的公式,此处不加绝对值,若点在视锥体外,距离为负数
if (Vector3.Dot(normal,pos) + dist <= 0)
{
return false;
}
}
return true;
}
//这里以左右剪裁面为例,其他可以自行求证
public bool TestCameraView2(Vector3 pos)
{
var camera = Camera.main;
var farClipPlane = camera.farClipPlane;
//w为相机远剪裁平面宽的一半
var w = Mathf.Tan(camera.fieldOfView * 0.5f * Mathf.Deg2Rad) * farClipPlane * camera.aspect;
//向量相加
Vector3 vR =farClipPlane * transform.forward + w * transform.right;
//向量相减
Vector3 vL =farClipPlane * transform.forward - w * transform.right;
//向量叉积,在左手坐标系遵从左手定则,右手坐标系遵从右手定则,unity为左手坐标系,所以遵从左手定则。
Vector3 RightPlane_N = Vector3.Cross(vR,transform.up);//视椎体右平面法线
Vector3 LeftPlane_N = Vector3.Cross(transform.up,vL);//视椎体左平面法线
//摄像机到物体的向量
var vect = pos - camera.transform.position;
if (Vector3.Dot(vect,RightPlane_N) > 0 && Vector3.Dot(vect,LeftPlane_N) > 0)
{
return true;
}
return false;
}
// Update is called once per frame
void Update()
{
}
}
- 上面只是以左右剪裁为例子,上下前后逻辑一样。运行结果与方法一一样。
总结
方法一每次运行会产生GC,(是unity早就一流的内部问题,就是因为每运行一次都会创建6个新的平面,很蛋疼,当时内部人员就是不优化),但是大大简化了裁剪算法,因为平面的计算由unity内部提供方法; 方法二基本的裁剪由自己实现,如果优化的够好,可以实现0GC,但是需要我们自己实现各种算法细节。 二者各有优劣,自行选择即可。