博弈论系列之耶鲁公开课学习（五）：纳什均衡之坏风气和银行挤兑

2020-05-19 1,186 阅读5分钟

本节课针对纳什均衡进行了进一步的深入讲解。

定义

策略组合

策略组合是一个集合，包含了每个参与人的一个已选策略。分别用 $s_1^*$ ， $s_2^*$ ，... $s_n^*$ 表示。

纳什均衡

纳什均衡（NE，Nash Equilibrium）是满足如下条件的一种策略组合，对于策略组合中任意一个参与人 $i$ ，他选择的策略 $s_i^*$ 是在其他参与人所选策略的最佳应对（BR）。

特点

不后悔（No regret）：每个人都不会为当时的决定产生后悔，因为已经是最佳应对。所有人都不会改变自己的策略，在其他人不改变策略的情况下，自己改变策略无法获得收益。

如何寻找纳什均衡

博弈矩阵如下图所示，共两个参与人。参与人1的策略集合为 $S_1=\{U,M,D\}$ ，参与人2的策略集合为 $S_2=\{L,C,R\}$ 。

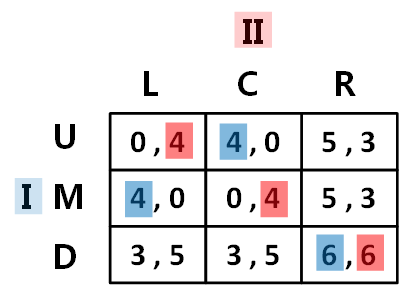
当参与人2选择 $s_2=L$ 时，参与人1的最佳应对是 $BR_1(L)=M$ 。
同理我们可以得到其他情况下的最佳应对： $BR_1(C)=U$ ， $BR_1(R)=D$ ， $BR_2(U)=L$ ， $BR_2(M)=C$ ， $BR_2(D)=R$ 。

我们用蓝框表示参与人1的BR，红框表示参与人2的BR。根据纳什均衡的定义， $NE=(D,R)$ 。此时参与1和参与2都达到了最佳应对。

值得注意的是：存在纳什均衡，不代表博弈的最终结果一定是纳什均衡。如果参与人1的信念是 $s_2=C$ ，那么参与人1的策略就是 $s_1=U$ 。而参与人2实际上选择的是R，那么此时策略组合就是 $(U,R)$ 。

如果将博弈改成如下:

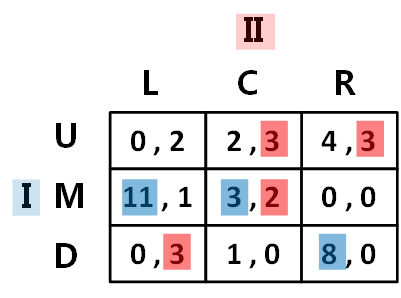
我们可以得到如下的最佳应对： $BR_1(L)=M$ ， $BR_1(C)=M$ ， $BR_1(R)=D$ ， $BR_2(U)=C,R$ ， $BR_2(M)=C$ ， $BR_2(D)=L$ 。此时的纳什均衡为 $NE=(M,C)$ 。

根据最佳应对我们发现，对于参与人1而言， $U$ 在任何情况下都不会是最佳应对。那么 $U$ 可以被剔除。当参与人2知道 $U$ 被剔除后，策略 $R$ 在任何情况下都不会是最佳应对，所以 $R$ 也需要被剔除。如果参与人1知道 $R$ 被剔除了，那么策略 $D$ 就要被剔除。如果策略 $D$ 被剔除了，策略 $L$ 就要被剔除。所以最后的策略组合只可能是 $(M,C)$ 。

请注意这里和第一个博弈的区别。纳什均衡是最佳应对的策略组合，所以一定不会被剔除，但不代表最终的博弈结果一定会落在纳什均衡上。

严格劣势与纳什均衡

此时我们回头来看囚徒困境。具体的收益矩阵我们复用第一讲的成绩博弈。

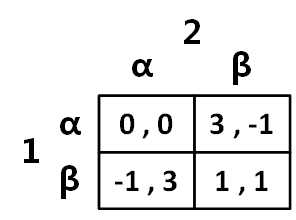
$\alpha$ 是严格优于 $\beta$ 的，所以 $NE=(\alpha,\alpha)$ 。

严格劣势策略一定不是最佳应对，所以一定不可能是纳什均衡。纳什均衡必须是最佳应对的策略组合。

严格劣势策略一定不会出现NE，那么弱劣势呢？

弱劣势与纳什均衡

我们看如下一个博弈。

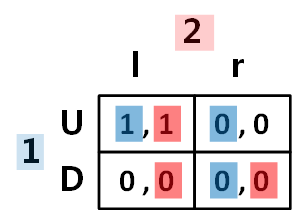
对于参与人1而言， $D$ 相比 $U$ 是弱劣势。对于参与人2而言，r比l是弱劣势。但是此时(D,r)仍然可以是对方的最佳应对，从而是NE。所以对于这个博弈而言，存在两个纳什均衡， $NE=(U,l)；NE=(D,r)$

投资博弈

本次博弈不再是两个参与人，而且很多人（在场所有学生）。所幸策略集合简单，每个人需要对一个项目进行投资，只有两种投资策略 $S=\{\$10，\$0\}$ 。收益如下：

U(\$0)=\$0

U(\$10)= \begin{cases}
$5, & 参与统计人数 \geq90\% \\
$-10, & 参与统计人数<90\%
\end{cases}

收益矩阵简写如下：

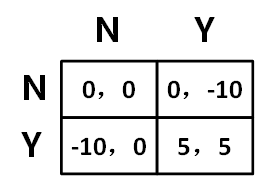
此博弈同样存在两个纳什均衡。一个是大家都不投资，一个是大家都投资。

在场学生第一次进行博弈时，约50%选择了投资，50%选择了不投资。第二次再进行博弈的时候，大部分都选择了不投资。我们发现博弈结果在渐渐朝向较差的不投资纳什均衡靠近。

那么如果第一次博弈的时候，有93%的人选择了投资呢？可以预见，博弈就将向较好的投资纳什均衡靠近。

结论：博弈的初始点会影响博弈最终结果。

同时我们可以发现，不投资的纳什均衡相比投资的纳什均衡是处于帕累托劣势。那么此时这个博弈就是一个协调博弈。

协调博弈

本节课的末尾引出了协调博弈。协调博弈就是博弈中存在多个能够进行帕累托排序纳什均衡的博弈。投资博弈中，就存在两个可帕累托排序的两个纳什均衡 $(N，N) < (Y，Y)$ 。那么此时，协调就体现出来了。我们可以通过协调使得人们达到更优的纳什均衡。

最经典的例子就是《美丽人生》中吉米·斯图尔特说服人们达成一种较优的NE，如果大家都相信银行，存钱进去，那么银行就能给大家带来利润。如果大家都不相信银行，去提款（银行挤兑），银行就会倒闭，大家也就没利润了。

那么囚徒困境是不是也能通过协调去选择更好的结果呢（都不坦白，就不用坐牢）？答案是否定的。因为在囚徒困境中，不坦白是一个严格劣势策略。你无法说服一个人去选择严格劣势策略，即使最终能达成更好的结果。

协调博弈可以通过协调，是因为纳什均衡中每个策略都是最佳应对，是能够使人信服的。