女神图开篇

本文讲解FM, FFM, DeepFM 算法,重点要先深刻理解FM算法。
FM
-
是什么:FM(Factorization Machine)因子分解机,最早是由Konstanz大学Steffen Rendle(现任职于Google)于2010年最早提出的,旨在解决稀疏数据下的特征组合问题。
-
针对的问题:类别特征是非常常见的,对类别特征一般先One-Hot编码。One-Hot编码的一个特点就是导致特征空间大。例如,商品品类有550维特征,一个categorical特征转换为550维数值特征,特征空间剧增。又比如在腾讯广告2020赛题中,广告所属行业(industry)有326种,(industry)这一个特征在one-hot转化后会变成326个特征,这些特征是非常稀疏的(326个特征只有一个是1,其它是0)。这种情况在真实场景中广泛存在。
-
解决上面问题的出发点:特征之间是有关系的。通过观察大量的样本数据可以发现,某些特征经过关联之后,与label之间的相关性就会提高。例如,“USA”与“Thanksgiving”、“China”与“Chinese New Year”这样的关联特征,对用户的点击有着正向的影响。引入特征的组合是非常有意义的。多个特征组合复杂度太高,一般用两个特征的组合
-
多项式模型是包含特征组合的最直观的模型。二阶组合模型如下:
其中,n代表样本的特征数量,
是第 i 个特征的值,
是模型参数。在多项式模型中,特征
和
的组合采用
表示,即
和
都非零时,组合特征
才有意义。
-
该模型问题:
- 特征数量为N,则该模型二次项参数为
个,复杂度太高
- 在数据稀疏性普遍存在的实际应用场景中,二次项参数的训练是很困难的。因为做One-Hot编码后的大部分特征都是0,
同时非0的样本少。训练样本的不足,很容易导致参数
不准确,最终将严重影响模型的性能。
- 特征数量为N,则该模型二次项参数为
-
解决的思路:数学分析。观察,所有二次项系数可以构成对称矩阵
,对称矩阵可以分解,
。每个参数
,注意其中
是特征
和
的组合系数,是标量;
是表示特征
的向量 。这就是FM模型的核心思想。则FM的模型方程为
-
该分解的物理意义:利用了推荐系统中的矩阵分解思想,实际就是LFM(latent factor model)隐因子模型。其中
是第
个特征的隐向量,隐向量的长度为
,包含
个描述特征的因子。这样二次项参数从原来的
个减少到
。
| 样本 | |||||
|---|---|---|---|---|---|
| 样本1 | 1 | 0 | 0 | 0 | 1 |
| 样本2 | 0 | 1 | 0 | 1 | 0 |
| 样本3 | 0 | 0 | 1 | 0 | 1 |
对于样本2: 的所有二次项组合为:
如果 取,用
表示
, 此时二次项组合可以转化为:
类比
- 该等式原来需要
才能计算,这样的样本很少。通过隐向量因子分解的思想,等价变形成右式,只用满足
即可。解决了原来存在的问题,且参数量变少。
此时样本2: 的特征组合可以表示为:
- 对比:注意我们是用所有的样本学习这些模型参数。原来学习参数
时样本1,2,3都用不上,
就学不出来,代表
和
特征无法组合。但是转化后可以间接计算组合特征。
- 可以利用SGD(Stochastic Gradient Descent)训练模型。FM参数训练的复杂度为
,FM可以在线性时间训练和预测,是一种非常高效的模型。
- 物理意义:转化后计算组合特征的物理意义是什么?注意这里我们公式之所以能这么化简,是因为我们做了假设:即每一个特征都可以用一个
维的隐向量来表示。
- 这个假设在实际中一定永远成立吗?显然不一定。例如 行业(industry)特征做one-hot后,不同行业都用
维向量表示还行,但此时性别(gender)特征又怎么能也用
维向量表示呢?这显然不太合理。若该假设有问题,则公式不成立。
- FM是一种比较灵活的模型,通过合适的特征变换方式,FM可以模拟二阶多项式核的SVM模型、MF模型、SVD++模型等
- 碎碎念:跟当初学习理解物理公式差不多,难理解的不是公式的数学推导,而是推导背后的物理意义。
FFM
-
是什么:FFM(Field-aware Factorization Machine)最初的概念来自Yu-Chin Juan与其比赛队员,是他们借鉴了来自Michael Jahrer的论文[14]中的field概念提出了FM的升级版模型。通过引入field的概念,FFM把相同性质的特征归于同一个field。(FFM原始论文)
-
碎碎念:深入理解FM算法的假设其实不难发现这个问题,通过我上面的分析自然会想到这种改进。竟然少有博客提到这点,说明理解思考不透彻。 其实应该直接看原始论文的,基本都是对论文的解读。这篇理解还不错 , 美团这篇讲得不太清楚
-
FFM模型方程:
FM算法所有特征都用同样长度的隐向量表示,
的隐向量为
;FFM算法把不同种类(即所说的不同filed)的用不同意义的隐向量表示。
-
简单理解举例:如上样本图。有326个行业(industry)feature,每个行业假如用20维隐向量表示,每一维向量有它的意义,比如某一维的值意义是代表行业工资or行业男女比(举例);但是有2个性别(gender)特征,每种性别如果也用20维向量表示,某一维的值意义和行业(industry)是不同的。所以要分种类,即326个行业(industry)特征
属于种类(filed),2个性别(gender)特征属于另一个种类(filed)。
-
特征两两组合时:
-
假设样本的
个特征属于
个field,则FFM模型参数量为
个。当
,即所有特征当作同一个种类(filed)时,FFM就变成FM了。
-
FFM核心问题:怎样在计算中体现不同的field?原来一个特征只有一个隐向量,现在一个特征有
个隐向量。一个特征使用哪个隐向量看另一个组合特征。
-
FFM原始论文核心方程:
公式中,
是
对应的field。如果是特征
组合,对应的是
。懂我意思吧。
-
原论文有一些训练和具体应用的说明,此处略,解读见 美团这篇
DeepFM
-
DeepFM基于google提出的 wide&deep 模型, 就是wide部分用FM,deep部分仍用DNN。(DeepFM原始论文)
-
这是wide&deep 模型图
-
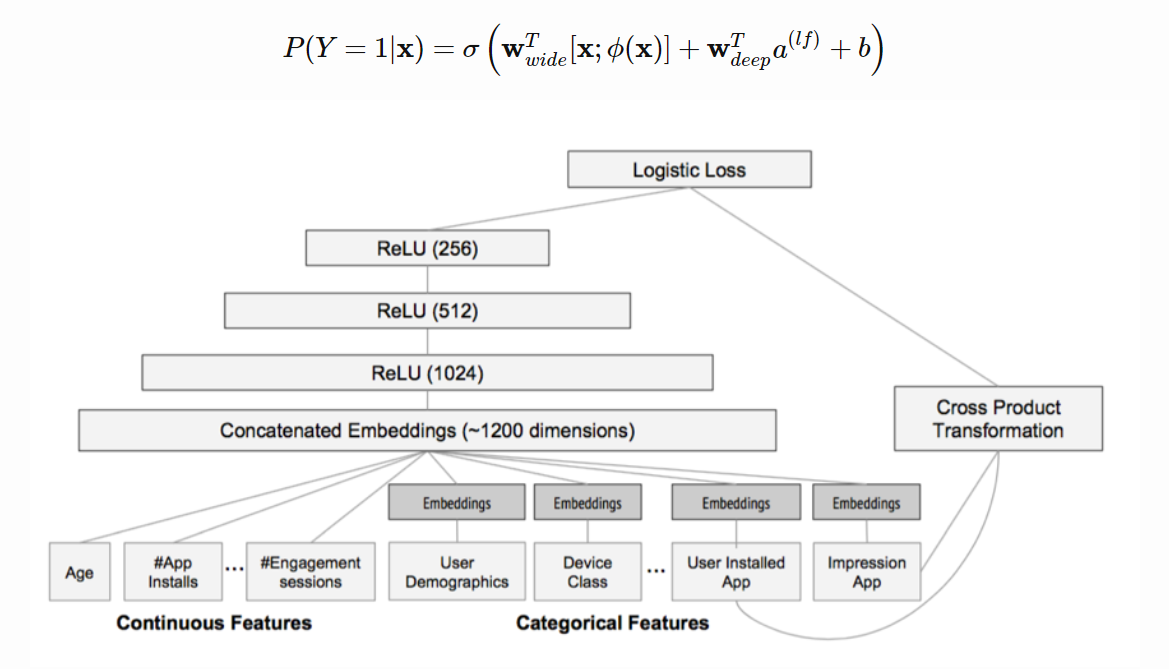
-
这是DeepFM模型图
-
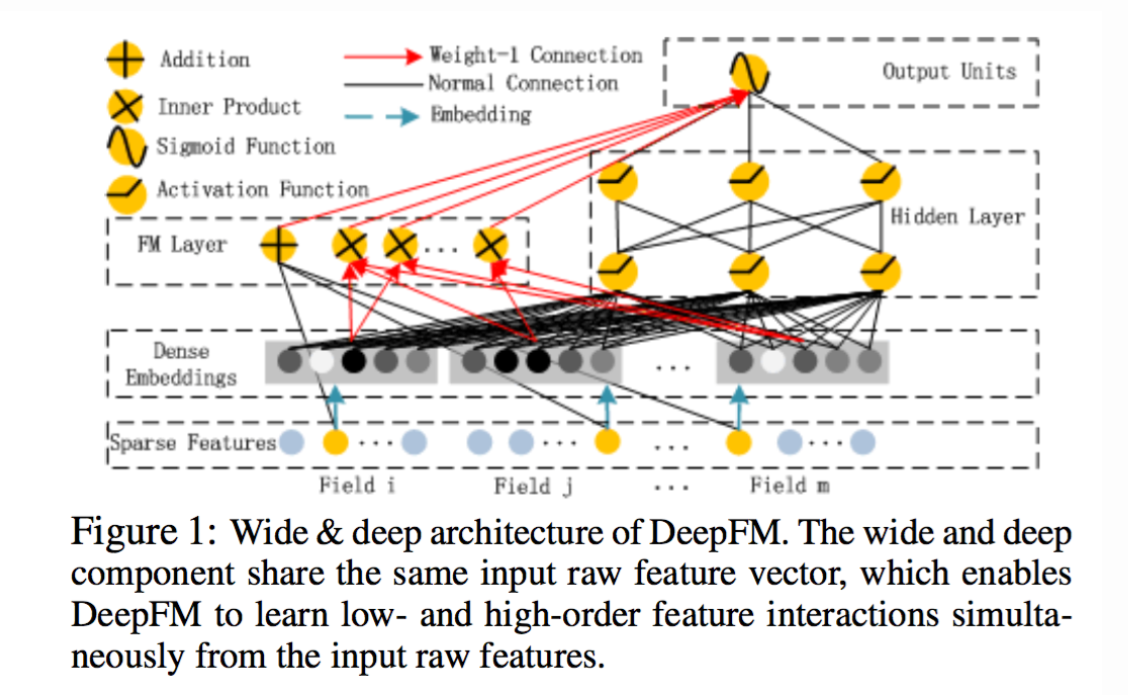
对比两图应该不难明白。
- wide和deep部分分别在学习不同阶的特征交叉,deep部分学到高阶交叉,而wide部分学到的是二阶交叉。
- 用FM替换了这里wide部分的二阶交叉,是得模型对高度稀疏的特征的建模更加有效,因为高度稀疏特征简单的叉积变换也难以有效地学到二阶交叉
- 因此,很自然的想法就是,用FM替换这里的二阶交叉,得到DeepFM模型 (参考)