【实战】手摸手教你Data Lab完成其函数体代码并“作为实验结果提交”。函数的功能与实现要求详细说明在相应函数和文件

首先介一下相关的文件的作用

README 有关实验细节的说明文件，请在开始实验前仔细阅读
bits.c 包含一组用于完成指定功能的函数的代码框架，需要你按要求补充完成其函数体代码并“作为实验结果提交”。函数的功能与实现要求详细说明在相应函数和文件首部的注释中（务必认真阅读和遵照说明完成实验）。
bits.h 头文件
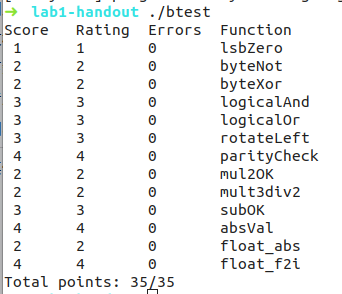
btest.c 实验结果测试工具，用于检查作为实验结果的 bits.c 中函数实现是否满足实验的功能正确性要求。
btest.h, decl.c, tests.c 生成 btest 程序的源文件
dlc 实验结果检查工具，用于判断作为实验结果的 bits.c 中函数实现是否满足实验的语法规则要求。
Makefile 生成 btest、fshow、ishow 等工具的 Make 文件
ishow.c 整型数据表示查看工具
fshow.c 浮点数据表示查看工具

int lsbZero(int x) {
  return x & ~1;
}

设计思路：将x的最低有效位置0,我的思路就是将x与0xfffffffe相与即可,而0xfffffffe就是~1,所以我的答案是x & ~1

int byteNot(int x, int n) {
  int mask = 0xff;
  int shift = n << 3;
  mask = mask << shift;
  return x ^ mask;
}

设计思路: 这一题的核心是:将某一位的数取反只需将这一位的数与1进行异或即可,而0与一位数进行异或还是原来的数,保持不变于是我们可以这么做,首先定义一个字节大小的掩码0xff,然后将掩码移位到你想要取反的字节处即可,而这个移位的距离也就是shift变量也就是n<<3,于是这一题就圆满解决啦!

int logicalAnd(int x, int y) {
 return !!x & !!y;
}

设计思路: &&操作符的含义是,如果两个操作数都为非0,那么结果为1,如果有一个操作数为0,那么结果为0 所以对于这一题,我的求解思路是:如果一个数非0,那么两次取非后的结果为1;如果一个数为0,那么两次取非后的结果为0 所以,我们对两个操作数都进行两次取非操作,再对得到的结果进行&运算,如果两个数均为1,那么结果为1,否则为0,最后就得到了正确的答案啦

int logicalOr(int x, int y) {
 return !!x | !!y;
}

这一题的思路大体上和上一题一样,唯一不同的是最后的处理是 | 运算,这样最后我们就的到了正确的结果啦

int rotateLeft(int x, int n) {
 int mask = ~(~0<<n);
 return (x << n) | ((x >> (32 + ~n + 1)) & mask);
}

这一题要求将x循环左移,我的思路是:首先获取x的最左边n位的值,然后将x左移n位后的值或上x最左边n位的值即可具体实现:获取x左边n位的值可以通过先对0取反,然后左移n位,然后再取反获得对应的n位掩码,然后将x左移(32-n)位并且与掩码相与即可最后再将得到的结果与x左移n位后的结果相或即可得到正确的答案

int parityCheck(int x) {
 x = x ^ (x >> 16);
 x = x ^ (x >> 8);
 x = x ^ (x >> 4);
 x = x ^ (x >> 2);
 x = x ^ (x >> 1);
 x = x & 0x1;
 return x;
}

这一题用到了非常巧妙的分治的思想,以及利用了异或运算的一些特性. 首先将x均分为两部分,左半部分与右半部分进行异或运算,这样如果对应的位为两个1,那么就消去了. 然后对低16位进行同样的操作,这样最后的结果中最低位如果是1就说明有奇数个1,否则说明有偶数个1.

int mult3div2(int x) {
 x = (x << 1) + x;
 int fix = (((x >> 31) & 0x1) &  (x & 0x1));
 return (x >> 1) + fix;
}

首先执行乘3的操作,具体做法就是先将x左移一位,然后加上x 然后执行除法的时候需要注意舍入的问题:如果最低位为1的话,那么除2是除不断的,这个时候要根据符号位来判断舍入的情况如果符号位为0,说明是正数,那么就要向下舍入,但是如果符号位为1,也就是负数,那么就要向上舍入,这里我通过一个fix修正变量来实现最后得到正确的答案

int mul2OK(int x) {
 return (((x >> 31) & 0x1)^((x >> 30) & 0x1)) ^ 0x1;
}

由于乘2的操作等价于左移1位,于是可以通过比较最高位和第二高位来进行判断如果相同,那么就说明没有溢出,如果不相同,那么就说明溢出了.

int subOK(int x, int y) {
 int sign1 = ((x >> 31) & 0x1) ^  ((y >> 31) & 0x1);
 int sign2 =  ((x >> 31) & 0x1) ^  (((x + ~y + 1) >> 31) & 0x1);
 return !(sign1 & sign2);
}

如果x与y的符号位相同,那么x-y是一定不会溢出的而当x与y符号位不同的时候,可能会产生溢出,这时发生溢出的条件就是,x与x-y的符号位也不同综上所述:当x与y符号位不同, 而且x与x-y符号位也不同的时候, 那么就代表溢出了按照这个思路可以很容易的写出对应的实现代码如下所示.顺利得到正确的答案

int absVal(int x) {
  int sign = x >> 31;
  return ((sign&(~x+1)) + ((~sign) & x));
}

求x的绝对值,那么就要区分正负,如果是非负数,那么绝对值就是本身,如果是负数,那么绝对值就是其相反数所以我们可以通过符号位来实现这个操作,如果符号位为1,就说明是负数,那么此时的sign变量由于是用补码表示,所以是一个32位全为1的数将sign与(~x+1)相与; 如果符号位为0,那么说明绝对值就是它本身,此时的sign变量值为0,于是将其取反与x相与. 最后将得到的结果相加即可得到正确的答案.

unsigned float_abs(unsigned uf) {
  int mask = ~(1 << 31);
  int x = uf & mask;
  if (x > 0x7f800000) {
      return uf;
  } else {
    return x;
  }
}

将符号位置0即可获得绝对值表示,但是这里需要重点判断是否位NaN,如果是NaN的话就得返回原数 NAN的具体判断方法如下所示:如果阶为全1,尾为非0的话,那么就是NAN,所以只用判断uf与掩码相与后的值与0x7f800000的大小, 如果大于,那么就是NAN,否则不是.如果是NAN,那么返回uf,否则,返回x.

int float_f2i(unsigned uf) {
    int sign = (uf >> 31) & 0x1;
    int exponent = (uf >> 23) & 0xff;
    int bias = exponent + ~126;
    int mask = ~(~0 << 23);
    int significant = uf & mask;

    if (!exponent || bias < 0) return 0;
    if (!(exponent ^ 0xff) || bias > 30) return (1 << 31);

    significant = significant | (1 << 23);
    if (bias > 23) {
        significant = significant << (bias - 23);
    } else {
        significant = significant >> (23 - bias);
    }
    if (sign) return ~significant + 1;
    else return significant;
}

这一题需要对IEEE754标准非常熟悉,首先提取出符号位(最高位),阶码(紧接着8位),尾数(最后面的23位) 然后需要清楚的知道一下几点:

零:阶码全0, 尾数全0
∞: 阶码全1, 尾数全0
NaN: 阶码全1, 尾数为非0
非规格化: 阶码为全0, 尾数为非0, 隐藏位为0
规格化: 阶码为1~254, 尾数最高位为隐藏位1

所以,如果阶码为0的话,那么这个数不是0就是非规格化,那么最后化成整数舍入后一定是0 如果bias = 阶码 - 127 < 0的话, 那么最后乘以2^bias次方的结果化成整数舍入后一定为0 如果阶码全1,那么不是NaN就是∞,那么最后的结果一定是0x80000000 如果bias > 30的话,那么对于一个int型的整数来说表示不了,所以会溢出,结果也是0x80000000 再剩下的情况就是可以表示了,我们就需要判断bias与23的大小关系了对significant补上隐藏的1,然后根据bias与23的大小关系进行移位运算,最后舍掉小数点后面的就得到最终结果了.