数据结构与算法之平衡二叉树

什么是平衡二叉树

• 定义：平衡二叉树是一种排序二叉树，其中每个结点的左子树与右子树的高度差之多为1（或-1）
• 高度平衡：要么它是一个空树，要么它的左子树和右子树的都是平衡二叉树，且左子树与右子树的深度之差的绝对值不超过1
• 平衡因子BF：我们将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子
• 认识平衡二叉树

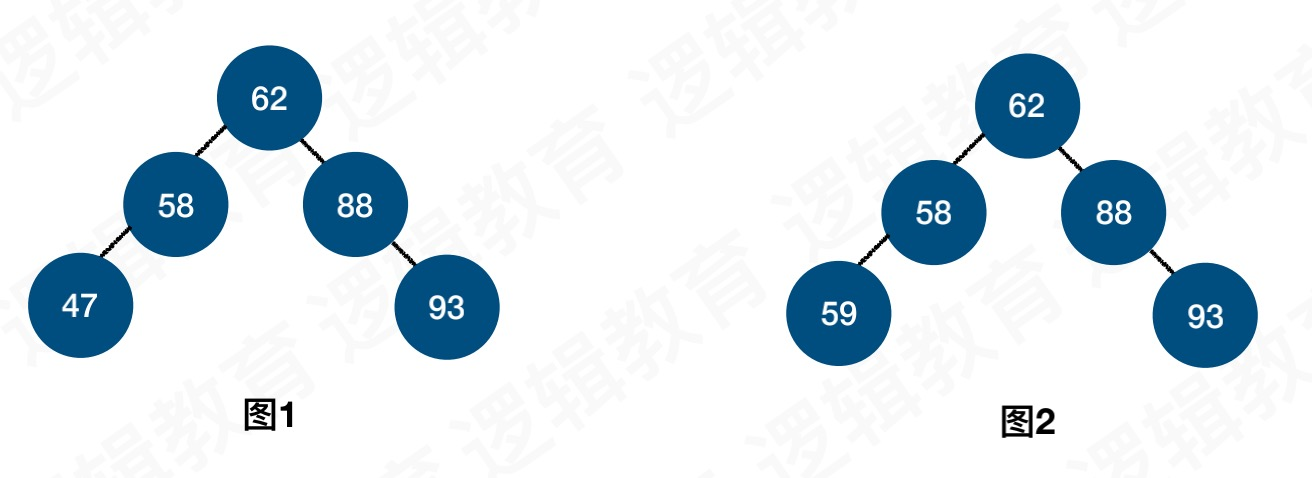
  其中图1是平衡二叉树，图2不是平衡二叉树，因为它不是二叉排序树

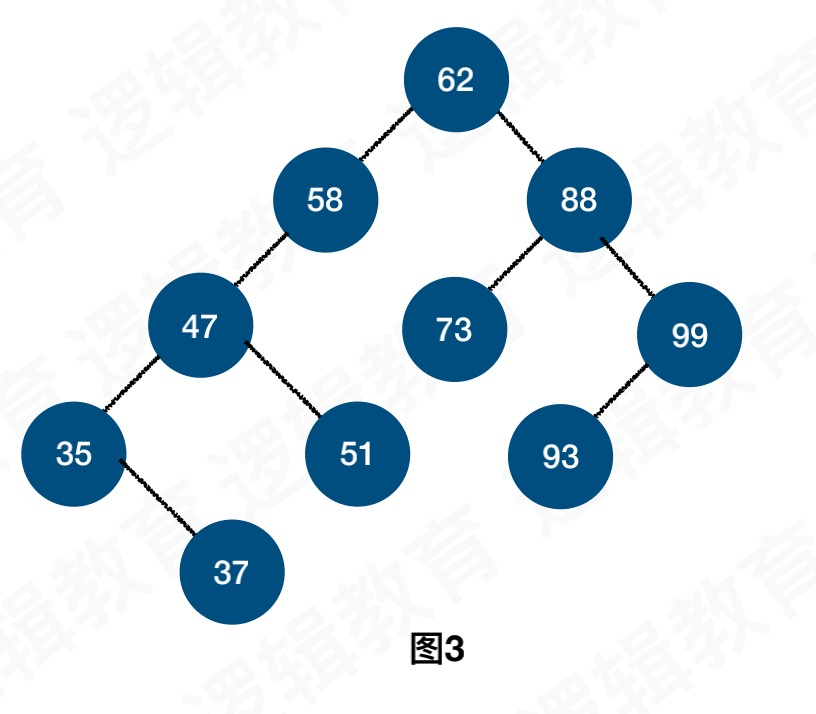
  图3也不是平衡二叉树，因为58节点的平衡因子BF为3，它大于1，所以不是

• 最小不平衡子树：距离插入节点最近的其平衡因子BF的绝对值大于1的节点为根的子树，我们称为最小不平衡子树

  
  

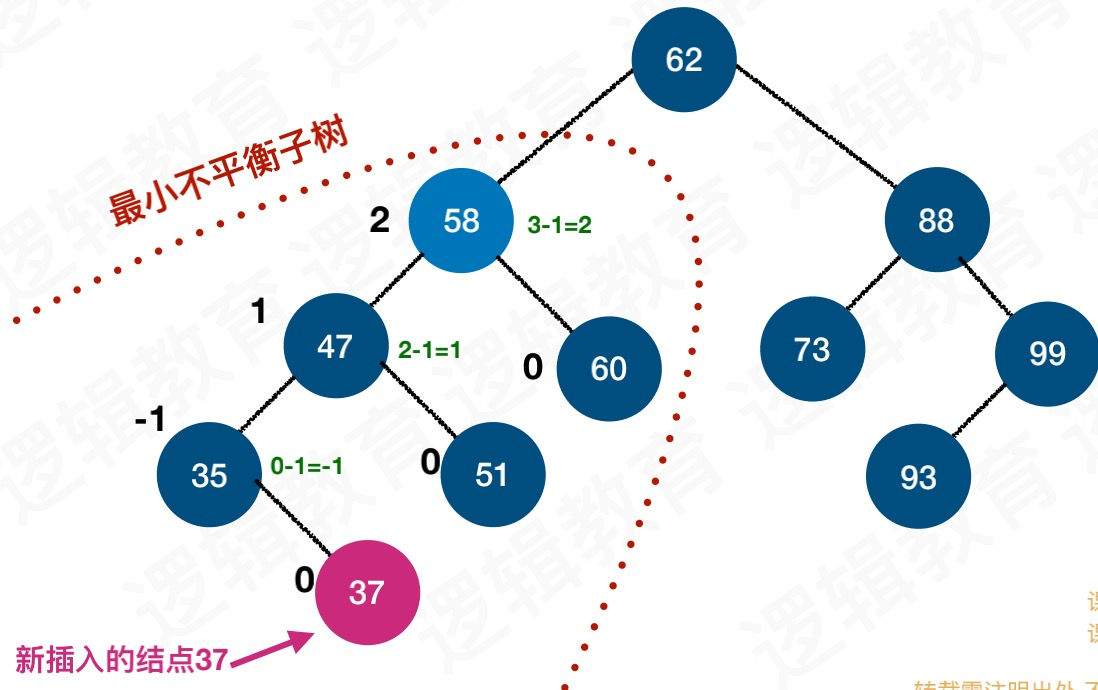
平衡二叉树的实现

设计思想

在构建二叉排序树的过程中，每当插入一个新的节点就要判断新插入的节点会不会破坏树的平衡，如果会则找到最小的不平衡子树，在保持二叉排序树的前提下，调整最小不平衡树中各节点之间的连接关系，进行相应的旋转，使之成为新的平衡子树。

图解实现过程

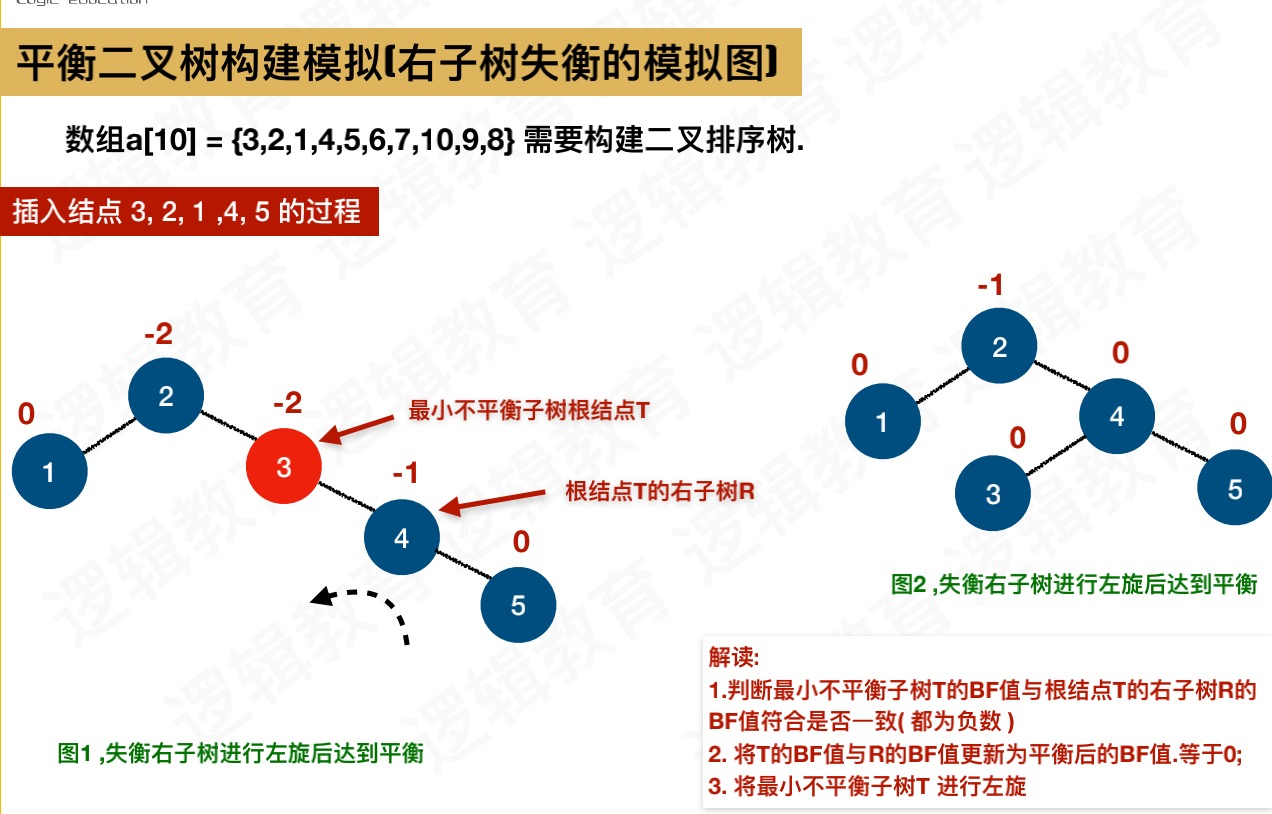
将数组a[10] = {3,2,1,4,5,6,7,10,9,8}构建成平衡二叉树

• 插入节点3、2、1，由于插入1节点导致3节点BF值大于1，所以需要有旋转

  
  

• 插入4节点，正常插入

  
  

• 插入5节点，由于3节点(是最小不平衡子树)的BF值为-2，绝对值大于1，所以3节点左旋转

  
  

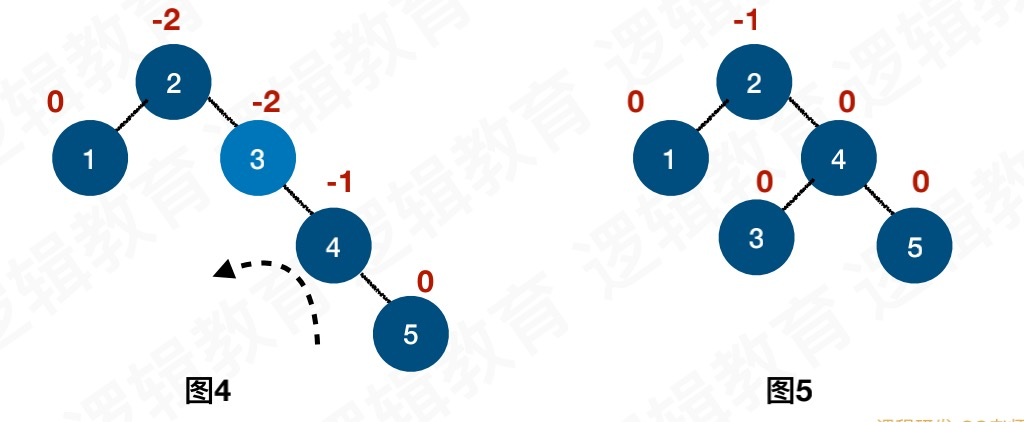
• 插入6节点，插入6节点导致2节点的BF值为-2，绝对值大于1，所以2节点左旋转

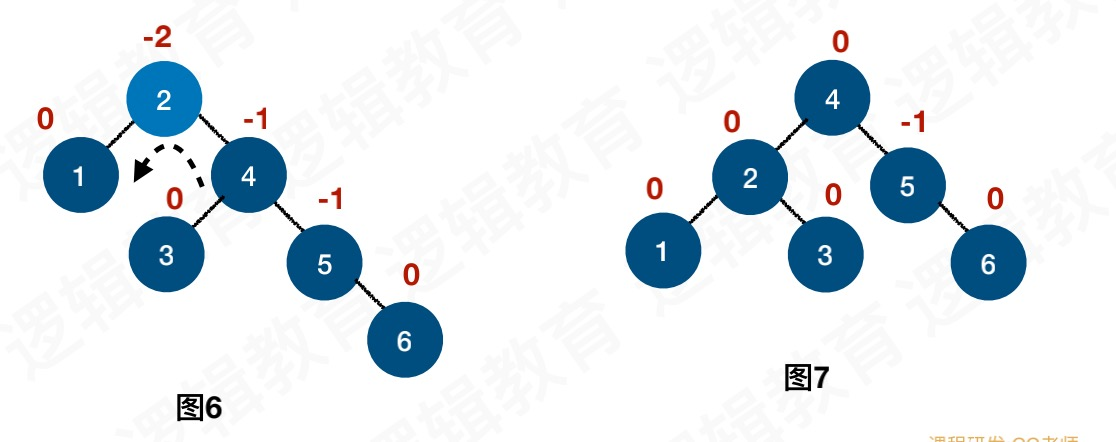
• 插入7节点，导致5节点的BF为-2，所以5节点左旋转

  
  

• 插入10节点，正常插入

  
  

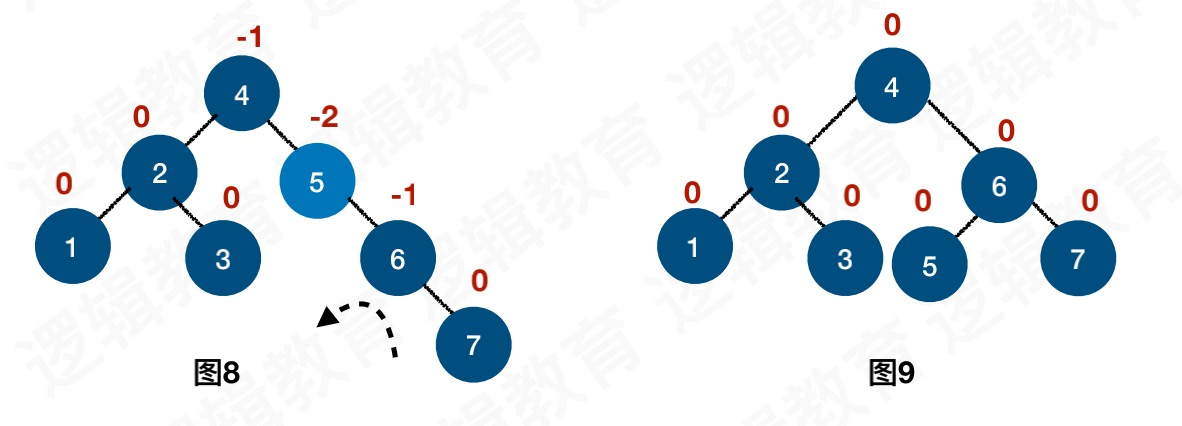
• 插入9节点，会导致7节点BF为-2，10节点BF为1，此时我们不能直接将10节点右旋转

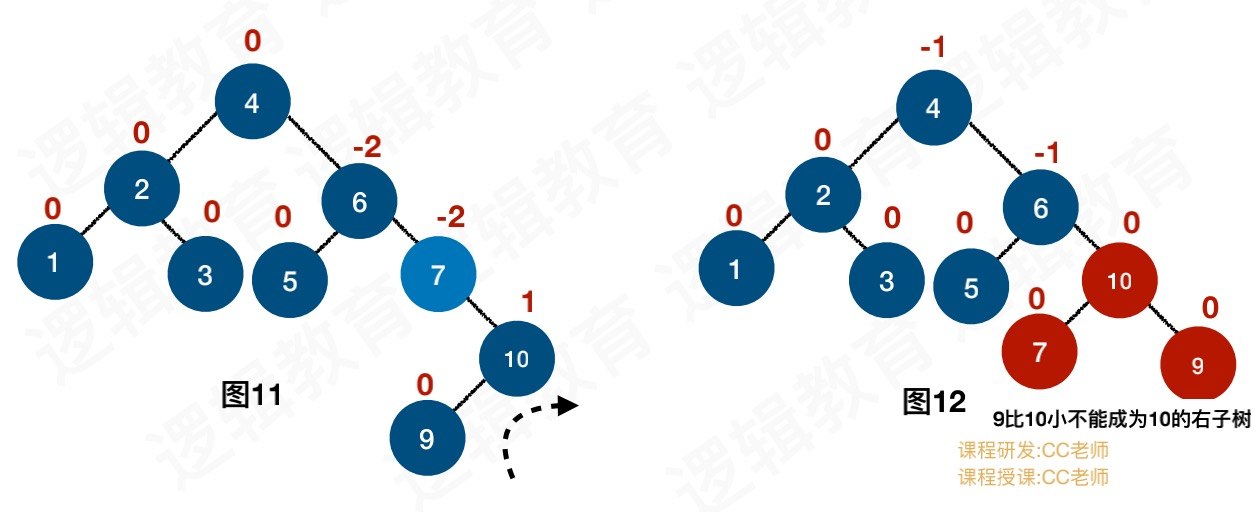
  否则造成非二叉排序树，因此我们要先左旋转，统一符号，然后再右旋转

  
  

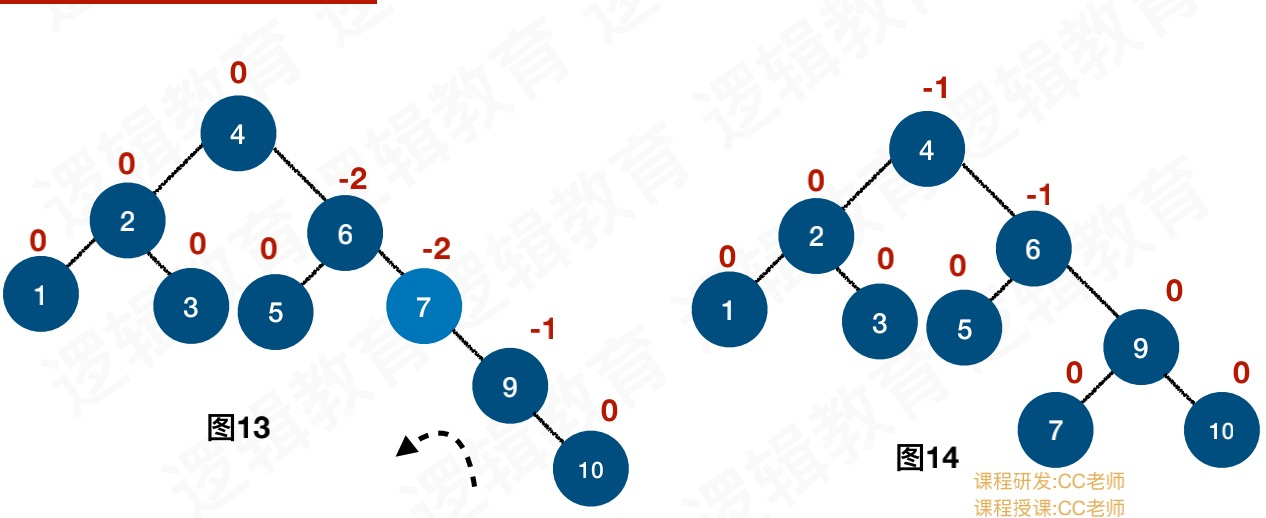
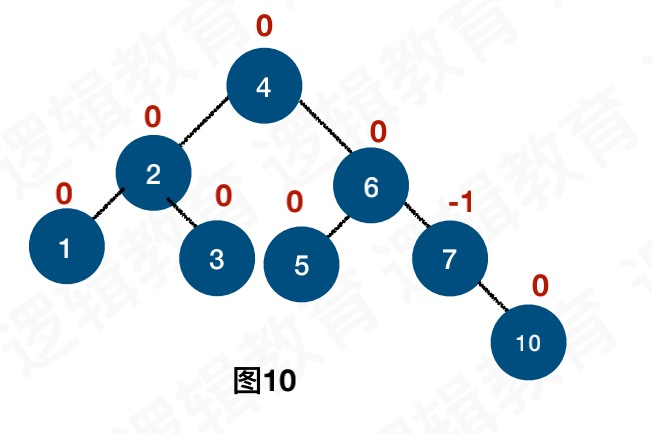
• 插入8节点，导致6节点的BF为-2，所以左旋转

  
  

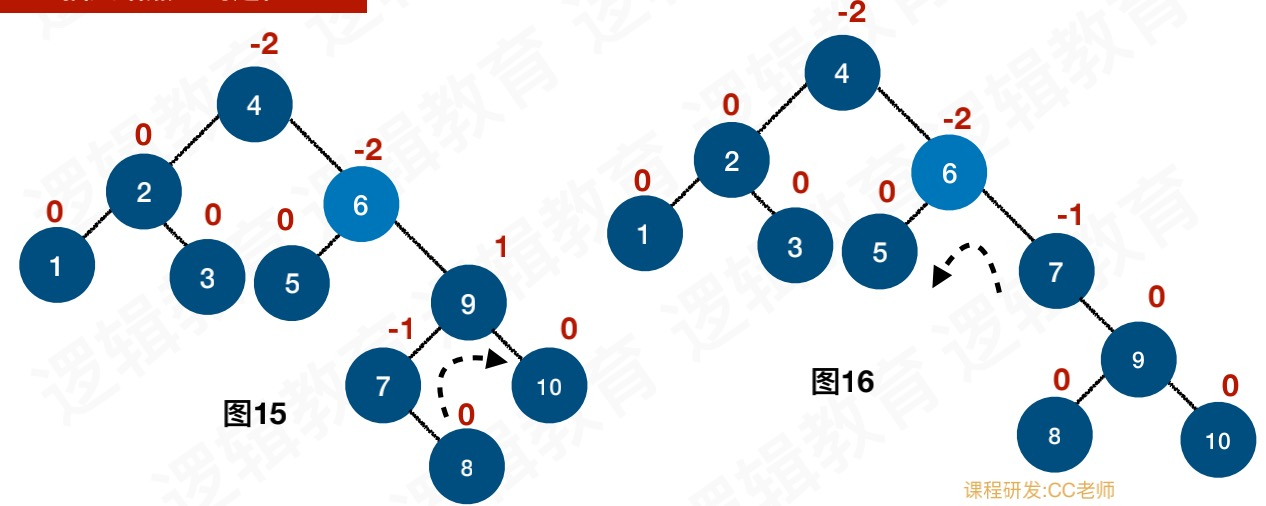
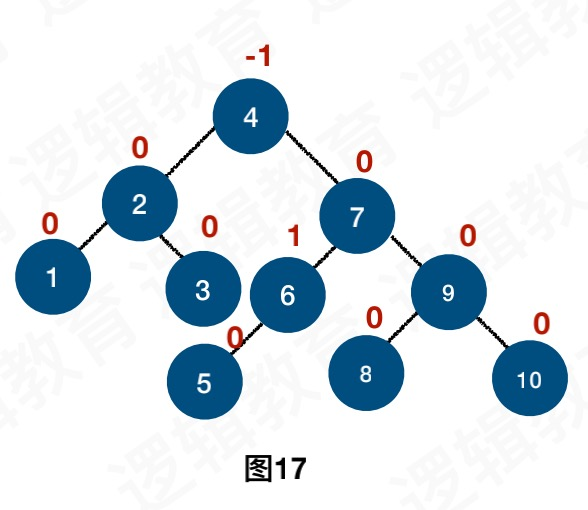
• 插入完成后

  
  

旋转规则

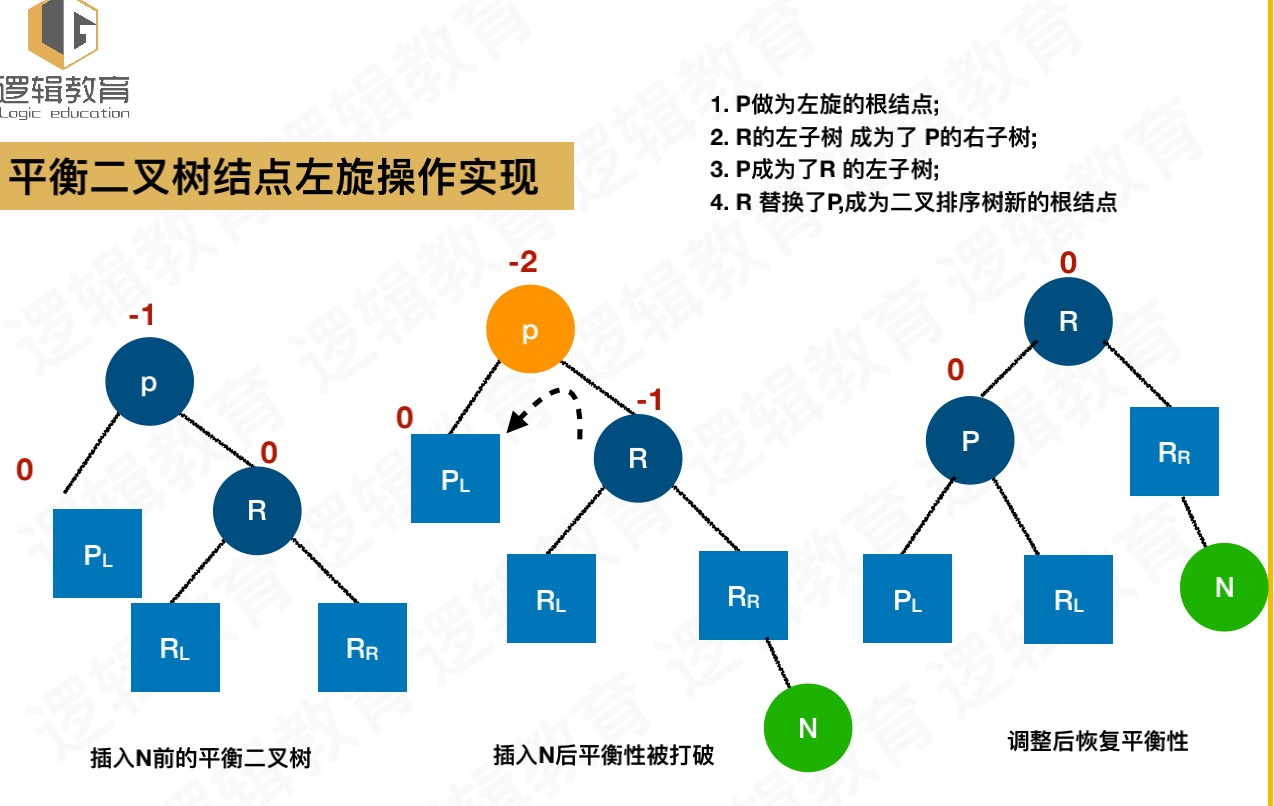
• 左旋转规则

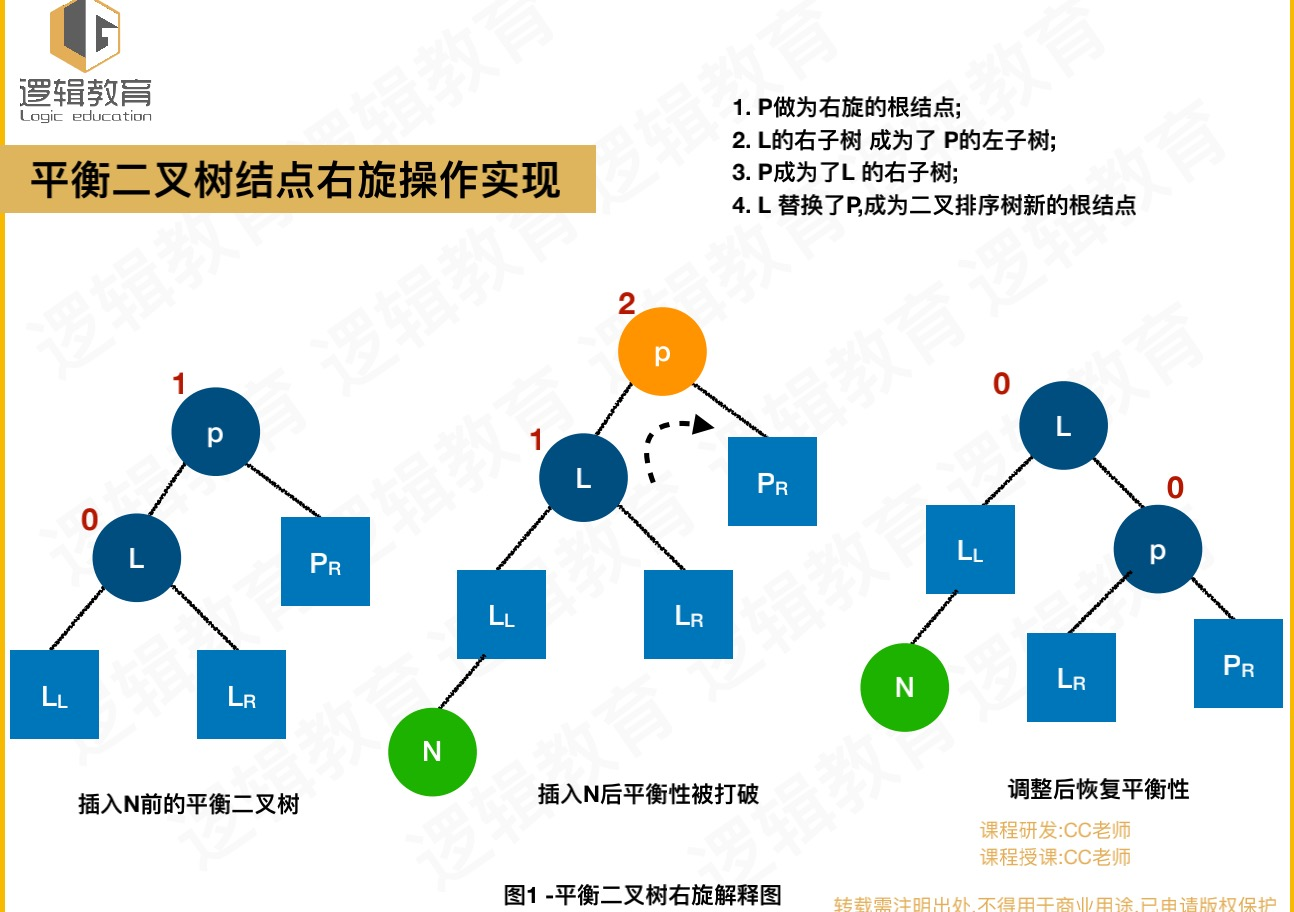
• 右旋转规则

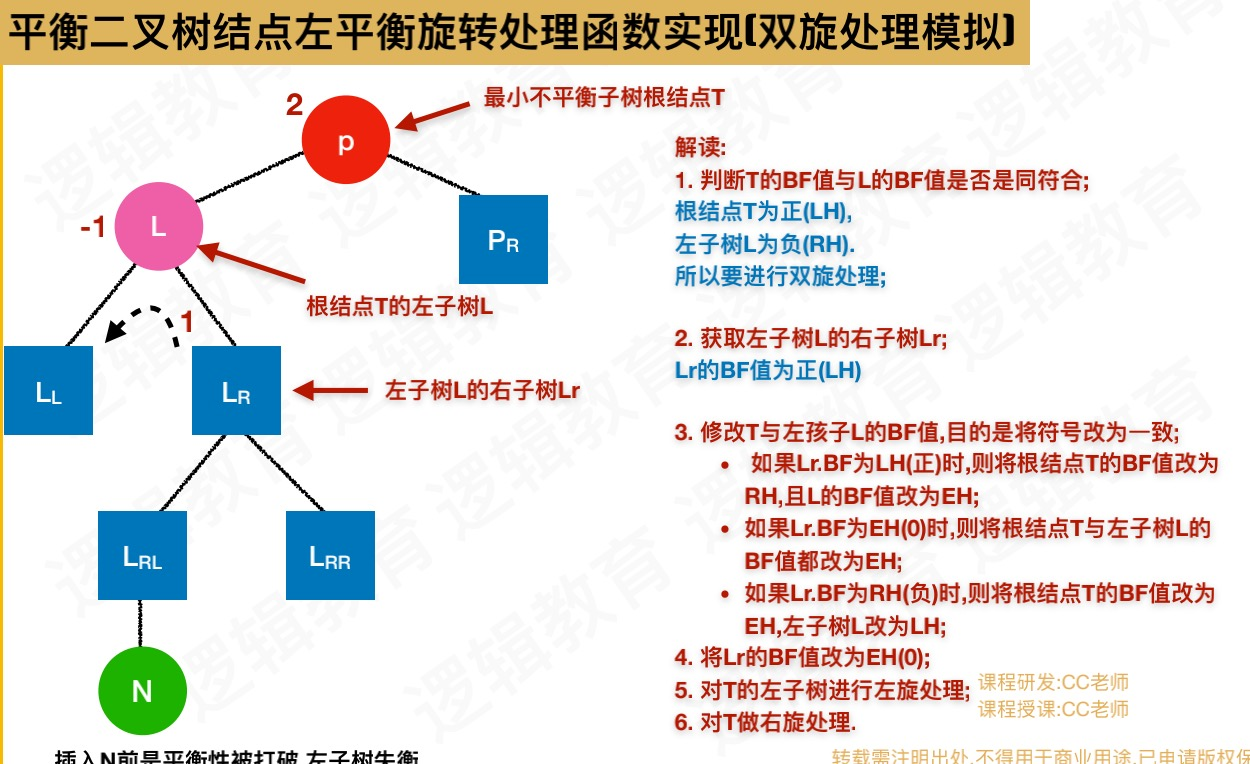
• 双旋转规则：定义3个常量，LH左高，EH等高，RH右高

核心代码实现

#pragma mark - 左旋转
/**
 思路：
    1、p指向根节点
    2、L指向p的左孩子
    3、L的右孩子成为p的左孩子
    4、L成为新的根节点
 */
void L_Rote(BiTree *p){
    BiTree L;
    //L指向p的左子树
    L = (*p)->leftChild;
    (*p)->leftChild = L->rightChild;
    L->rightChild = *p;
    *p = L;
    
}
#pragma mark - 右旋转
/**
 思路：
    1、p指向根节点
    2、R指向p的右孩子
    3、R的左孩子成为p的右孩子
    4、R成为新的根节点
 */
void R_Rote(BiTree *p){
    BiTree R;
    //R指向p的右子树
    R = (*p)->rightChild;
    (*p)->rightChild = R->leftChild;
    R->leftChild = *p;
    *p = R;
    
}
#define LH +1 /*  左高 */
#define EH 0  /*  等高 */
#define RH -1 /*  右高 */

void LeftBalance(BiTree *T){
    BiTree L,Lr;
    L = (*T)->leftChild;
    switch (L->bf) {
        case LH:
            (*T)->bf = L->bf = EH;
            //右旋
            R_Rote(T);
            break;
        case RH:
            Lr = L->rightChild;
            switch (Lr->bf) {
                case LH://统一符号
                    (*T)->bf = RH;
                    L->bf = EH;
                    break;
                case EH:
                    (*T)->bf = L->bf = EH;
                    break;
                case RH:
                    (*T)->bf = EH;
                    L->bf = LH;
                    break;
                    
                default:
                    break;
            }
            Lr->bf=EH;
            //对T的左子树作左旋平衡处理
            L_Rote(&(*T)->leftChild);
            //对T作右旋平衡处理
            R_Rote(T);
            break;
            
        default:
            break;
    }
}

void RightBlance(BiTree *T){
    BiTree R,Rl;
    R = (*T)->rightChild;
    switch (R->bf) {
        case LH:
            Rl = R->leftChild;
            switch (Rl->bf) {
                case LH:
                    (*T)->bf = EH;
                    R->bf = RH;
                    break;
                case EH:
                    (*T)->bf = R->bf = EH;
                case RH:
                    (*T)->bf = LH;
                    R->bf = EH;
                    break;
                    
                default:
                    break;
            }
            Rl->bf = EH;
            R_Rote(&(*T)->leftChild);
            L_Rote(T);
            break;
        case RH:
            (*T)->bf = R->bf = EH;
            //左旋转
            L_Rote(T);
            break;
            
        default:
            break;
    }
}