数据结构和算法-- 二叉排序树

二叉排序树

定义

二叉排序树(Binary Sort Tree),又称为二叉查找树.它或者是一颗空树.或者是一颗 具有下列列性质的二叉树;

• 若它的左⼦子树不空,则左⼦子树上所有结点的值均⼩小于它的根结构的值;
• 若它的右⼦子树不空,则右⼦子树上的所有结点的值均大于它的根结点的值;
• 它的左右⼦子树也分别是⼆叉排序树;

结点结构

/二叉树的二叉链表结点结构定义
//结点结构
typedef  struct BiTNode
{
    //结点数据
    int data;
    //左右孩子指针
    struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

假设有下面一个二叉排序树

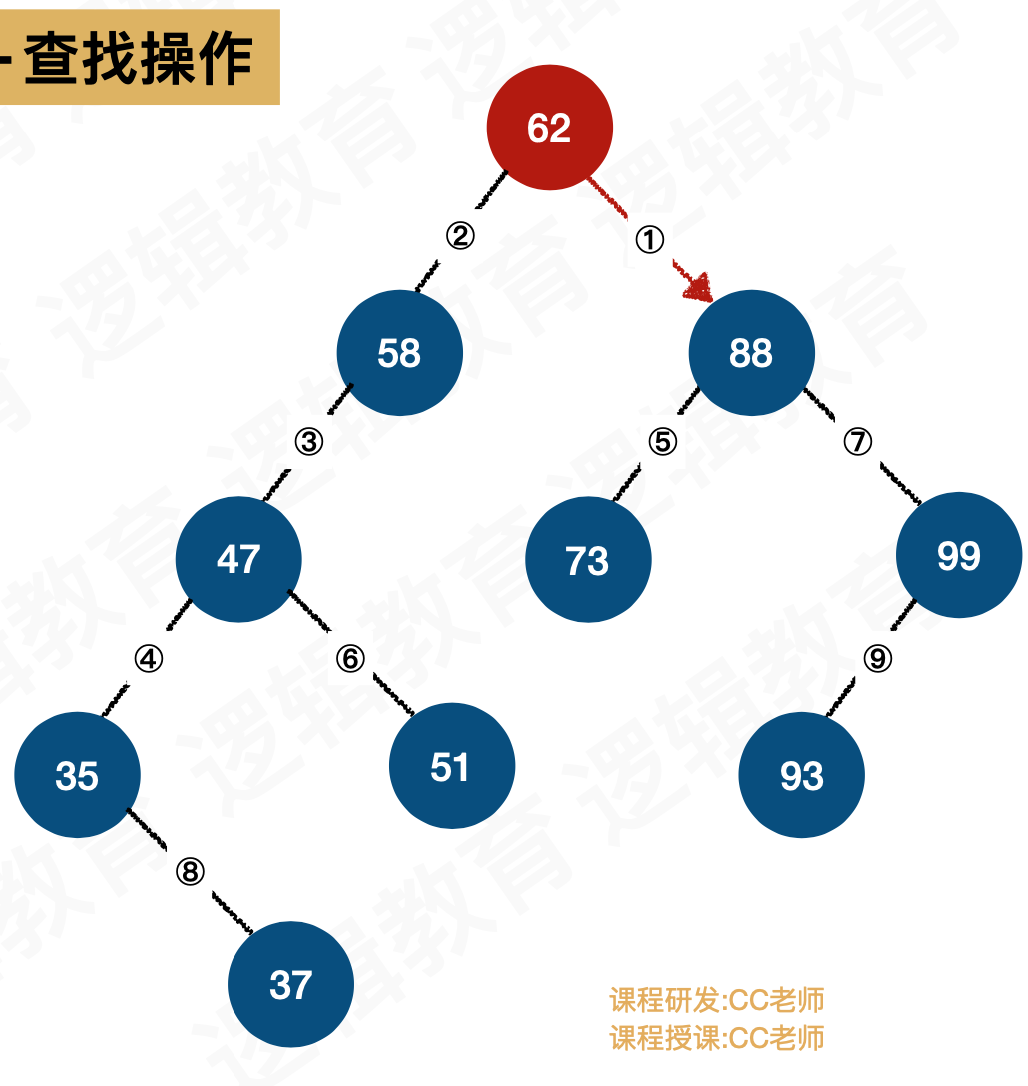
查找

在该树中找到key = 93的结点，模拟查找过程：

• 第1次: 判断62是否等于key,不等于则将查找范围 缩⼩小到右⼦子树;
• 第2次: 判断88是否等于key,不等于则将查找范围缩小到右⼦子树；
• 第3次: 判断99是否等于key不不等于则将查找缩⼩ 到左⼦子树；
• 第4次: 判断93是否等于key,成功;则返回TRUE；

//1.二叉排序树--查找
/*
 递归查找二叉排序树T中,是否存在key;
 指针f指向T的双亲,器初始值为NULL;
 若查找成功,则指针p指向该数据元素的结点,并且返回TRUE;
 若指针p指向查找路径上访问的最后一个结点则返回FALSE;
 */
Status SearchBST(BiTree T,int key,BiTree f, BiTree *p){
   
    if (!T)    /*  查找不成功 */
    {
        *p = f;
        return FALSE;
    }
    else if (key==T->data) /*  查找成功 */
    {
        *p = T;
        return TRUE;
    }
    else if (key<T->data)
        return SearchBST(T->lchild, key, T, p);  /*  在左子树中继续查找 */
    else
        return SearchBST(T->rchild, key, T, p);  /*  在右子树中继续查找 */
}

插入

向二叉排序树中查找关键字95;如果不不存在该记录则插⼊入到95到二叉排序树中

• 先按照二叉排序树的查找流程，看能否找到值为95的结点，如果找到则不用插入
• 如果在该树中找不到，则说明可以插入，并记录下跟95值最接近的结点p
• 创建一个结点s，判断p结点的值如果比95大，那么就将s插入到p的右孩子中，如果比95小，那么就将s插入到p的左孩子中

删除

二叉排序树删除结点会出现的3种情况:

• 1、删除叶⼦子结点，直接删除就行了
• 2、删除仅有左或者右⼦子树的结点
  • 仅有左子树，那么只需将左孩子放到原来位置即可
  • 仅有右孩子，那么只需将右孩子放到原来位置即可
• 3、删除左右⼦子树都有的结点
  • 找到右孩子的最大结点s，然后放到原来位置后
  • 如果s的双亲结点不是待删除结点，那么就将s的右孩子置为s的双亲结点左孩子
  • 如果s的双亲结点是待删除结点，那么就将s的左节点置为s双亲结点的右孩子

//3.从二叉排序树中删除结点p,并重接它的左或者右子树;
Status Delete(BiTree *p){
    
    BiTree temp,s;
    if((*p)->rchild == NULL){
        //情况1: 如果当前删除的结点,右子树为空.那么则只需要重新连接它的左子树;
        //①将结点p临时存储到temp中;
        temp = *p;
        //②将p指向到p的左子树上;
        *p = (*p)->lchild;
        //③释放需要删除的temp结点;
        free(temp);
        
    }else if((*p)->lchild == NULL){
        
        //情况2:如果当前删除的结点,左子树为空.那么则只需要重新连接它的右子树;
        //①将结点p存储到temp中;
        temp = *p;
        //②将p指向到p的右子树上;
        *p = (*p)->rchild;
        //③释放需要删除的temp结点
        free(temp);
    }else{
        
        //情况③:删除的当前结点的左右子树均不为空;
       
        //①将结点p存储到临时变量temp, 并且让结点s指向p的左子树
        temp = *p;
        s = (*p)->lchild;
      
        //②将s指针,向右到尽头(目的是找到待删结点的前驱)
        //-在待删除的结点的左子树中,从右边找到直接前驱
        //-使用`temp`保存好直接前驱的双亲结点
        while (s->rchild) {
            temp = s;
            s = s->rchild;
        }
        
        //③将要删除的结点p数据赋值成s->data;
        (*p)->data = s->data;
        
        //④重连子树
        //-如果temp 不等于p,则将S->lchild 赋值给temp->rchild
        //-如果temp 等于p,则将S->lchild 赋值给temp->lchild
        if(temp != *p)
            temp->rchild = s->lchild;
        else
            temp->lchild = s->lchild;
        
        //⑤删除s指向的结点; free(s)
        free(s);
    }
    
    return  TRUE;
}

//4.查找结点,并将其在二叉排序中删除;
/* 若二叉排序树T中存在关键字等于key的数据元素时，则删除该数据元素结点, */
/* 并返回TRUE；否则返回FALSE。 */
Status DeleteBST(BiTree *T,int key)
{
    //不存在关键字等于key的数据元素
    if(!*T)
        return FALSE;
    else
    {
        //找到关键字等于key的数据元素
        if (key==(*T)->data)
            return Delete(T);
        else if (key<(*T)->data)
            //关键字key小于当前结点,则缩小查找范围到它的左子树;
            return DeleteBST(&(*T)->lchild,key);
        else
            //关键字key大于当前结点,则缩小查找范围到它的右子树;
            return DeleteBST(&(*T)->rchild,key);
        
    }
}