这是普通数列求最大和的子数列的升级版。

普通版使用Kadane算法实现动态规划的思想

• 1. 非空数列情况下：dp[i] 表示以下标i结尾的数列的最大和，状态转移方程表示为: dp[i] = value[i] + max( 0, dp[i-1]),其中value[i]表示下标i的值。 最终结果是在一次循环中，最大的dp值
• 2. 可为空情况下：dp[i] = max(0, value[i] + dp[i-1])

代码如下:

//非空情况
int kadaneAlgorithNotEmpty (int[] nums) {
    if (nums.length == 0) {
        return 0;
    }
    int maxSoFar = nums[0];
    int maxTotal = nums[0];
    for (int i=1; i<nums.length; i++) {
        maxSoFar = nums[i] + Math.max(0, maxSoFar);
        maxTotal = Math.max(maxTotal, maxSoFar);
    }
    return maxTotal;
}

//可为空情况
int kadaneAlgorithm (int[] nums) {
    if (nums.length == 0) {
        return 0;
    }
    
    int maxSoFar = 0;
    int maxTotal = 0;
    for(int i=0; i<nums.length; i++) {
        maxSoFar = Math.max(0, nums[i] + maxSoFar);
        maxTotal = Math.max(maxTotal, maxSoFar);
    }
    return maxTotal;
}

而要解决环形的最大和的子数列，此时满足要求的子数列分成两种情况：

• 1. 最大和的子数列在原数列中：使用上述Kadane算法计算得出:maxSumSequential
• 2. 最大和的子数列在环形数列中：此时除了最大和的子数列，剩余的是最小和的连续子数列，所以这个maxSumNotSequential = sumTotal - minSum;
• 3. 极端情况，因为是非空子数列，所以如果全为负数时，2中的sumTotal = minSum,此时应该选择1中的maxSumSequential才对. 如下图所示：

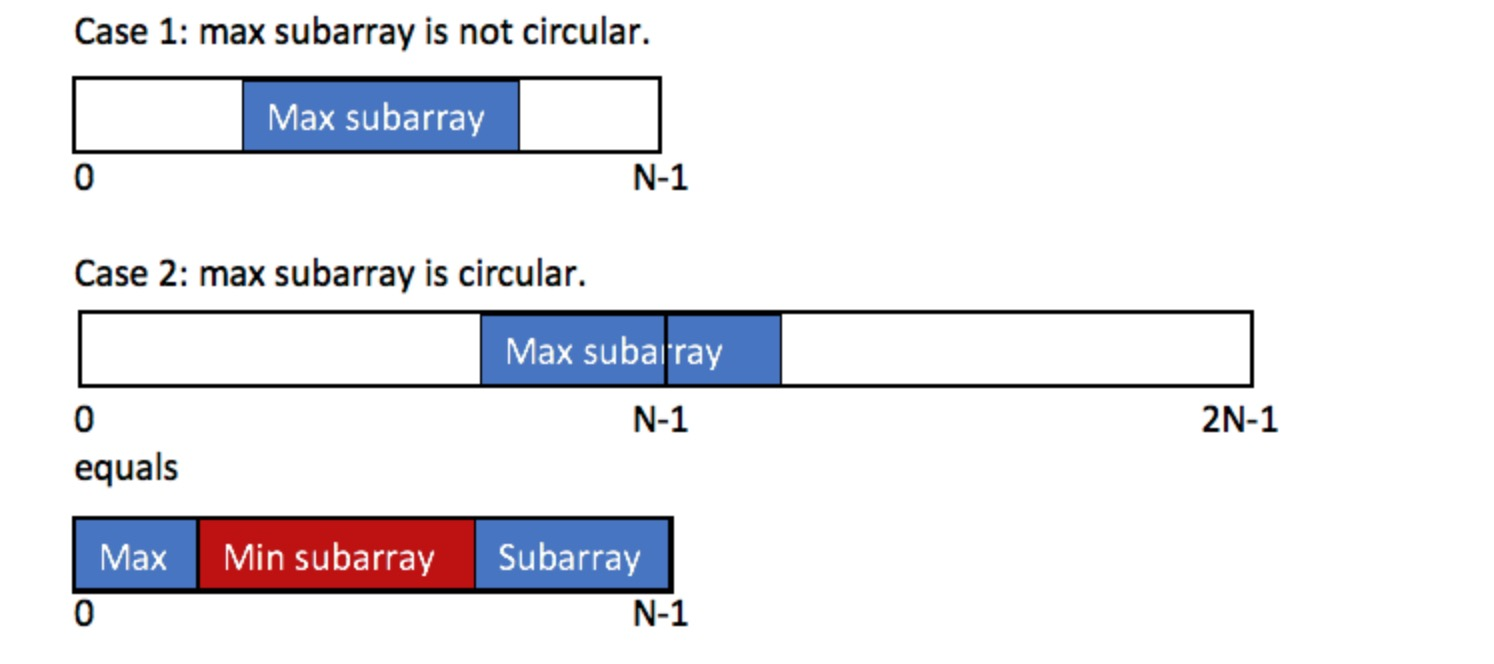
代码如下:

int circleKadaneAlgorithm (int[] nums) {
    if (nums.length == 0) {
        return 0;
    }
    int maxSoFar = nums[0];
    int maxTotal = nums[0];
    int minSoFar = nums[0];
    int minTotal = nums[0];
    
    int sum = nums[0];
    
    for (int i=1; i<nums.length; i++) {
        int num = nums[i];
        maxSoFar = num + Math.max(0, maxSoFar);
        maxTotal = Math.max(maxTotal, maxSoFar);
        
        minSoFar = num + Math.min(0, minSoFar);
        minTotal = Math.min(minTotal, minSoFar);
        
        sum += num;
    }
    
    if (sum == minTotal) {
        return maxTotal;
    }
    return Math.max(maxTotal, sum - minTotal);
}