想必大家都知道栈是一种先进后出的数据结构,那么单调栈有搞啥事情.....其实没啥子东西,就是学计算机的怕别人抢他饭碗造出来的专有名词。比如其形状如一根铁柱对折,尖端处作对刃刀这么一段话,这不就是剪刀么,说那么多干啥。

闲话少叙,咱们书归正传
其实单调栈是对栈中内容的描述,栈中的数据具有单调性,因而得名.单调栈由于其特殊性常用来解决比当前元素大的下一个(上一个)元素。
举个栗子,对于数组[2,1,2,4,3],你返回数组 [4,2,4,-1,-1]。 解释一下:第⼀个 2 后⾯⽐ 2 ⼤的数是 4; 1 后⾯⽐ 1 ⼤的数是 2;第⼆个 2 后⾯ ⽐ 2 ⼤的数是 4; 4 后⾯没有⽐ 4 ⼤的数,填 -1;3 后⾯没有⽐ 3 ⼤的数,填 -1。
画个图粘上代码咱们再唠
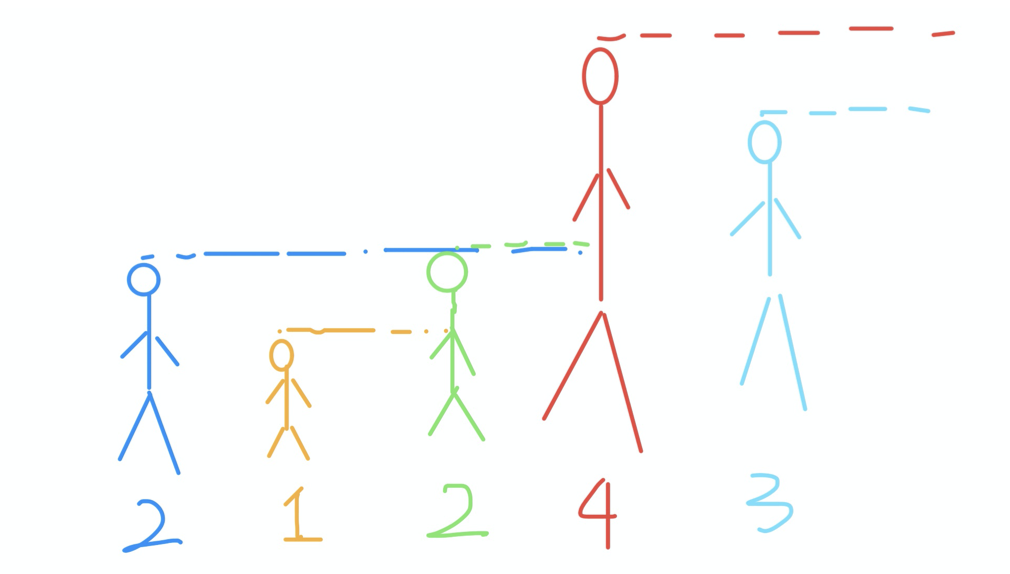
从上图可以看出,数组下标是0,1,2的三个值其实是看不见下标是4的值,因为被数组下标值为3的值挡住了,所以要将下标值是4的值从栈中弹出。其次,再来分析下数组下标为0的点,从下标为0的位置向“后”望去,需要将下标为1和下标为2的值出栈,这样才可以看到下标为3的值。以上两个说明都表示了会出栈小于等于当前元素的值
public int[] NGE(int nums[]){
int len=nums.length;
int res[]=new int[len];
Stack<Integer> stack=new Stack<>();
for(int i=len-1;i>=0;i--)
{
while(!stack.isEmpty() && stack.peek()<=nums[i])
stack.pop();
res[i]=stack.isEmpty()?-1:stack.peek();
stack.push(nums[i]);
}
return res;
}
- 从后向前来遍历才可以保证可以找到是下一个比当前元素大
- while循环的作用是将小于该节点的所有值都删除,保证了栈的单调性,这时从栈顶到栈底是单调增
上面的代码看明白了,我们刷几道Leetcode
首先是Leetcode739题,题目链接我放这里了每日温度,方便各位食用
这道题目是上面模型的简单变形,求的是比当前元素大的下一个值和当前元素的距离,*所以我们在栈中存放的将是数组下标,而不再是值,这样将当前元素的下标和栈顶元素的下标相减就是距离
public int[] dailyTemperatures(int[] T) {
int res[]=new int[T.length];
Stack<Integer> stack=new Stack<>();
for(int i=T.length-1;i>=0;i--)
{
while(!stack.isEmpty() && T[stack.peek()]<=T[i])
stack.pop();
res[i]=stack.isEmpty()?0:stack.peek()-i;
//存放的是下标
stack.push(i);
}
return res;
}
再来一道是Leetcode1019,链表中的下一个更大节点
链表的话是不能从后向前遍历(这里自然是单链表),那么咱就暴露的逆置一下,再从前向后遍历逆置后的链表,这样就达到了从后向前逆置链表的目的。逆置链表有递归和非递归两种方法,这里大家就自行解决。

class Solution {
int len=0;
//链表的逆置
public ListNode reverse(ListNode head)
{
len++;//计数求链表的长度
if(head==null || head.next==null) return head;
ListNode tail=reverse(head.next);
head.next.next=head;
head.next=null;
return tail;
}
public int[] nextLargerNodes(ListNode head) {
ListNode newHead=reverse(head);
int res[]=new int[len];
Stack<Integer> stack=new Stack<>();
int index=len-1;
for(ListNode cur=newHead;cur!=null;cur=cur.next)
{
while(!stack.isEmpty() && stack.peek()<=cur.val)
stack.pop();
//逆向给数组赋值
res[index--]=stack.isEmpty()?0:stack.peek();
stack.push(cur.val);
}
return res;
}
}
hhhh,写到这里不得不感觉Leetcode出题人的脑洞是真的大,而且为啥不将相同的题目放在一起呢?
来来来,开车了,Leetcode 503,下一个更大元素 II
循环数组的下一个可就有意思了,这里的“下一个”即可能出现在该元素前,还可能出现在该元素后。解决办法就是将原始数组“翻倍”,就是在后⾯再接⼀个原始数组,这样的话,按照之前“⽐⾝⾼”的流程,每个元素不仅可以⽐较⾃⼰右边的元素,⽽且也可以和左边的元素⽐较了。
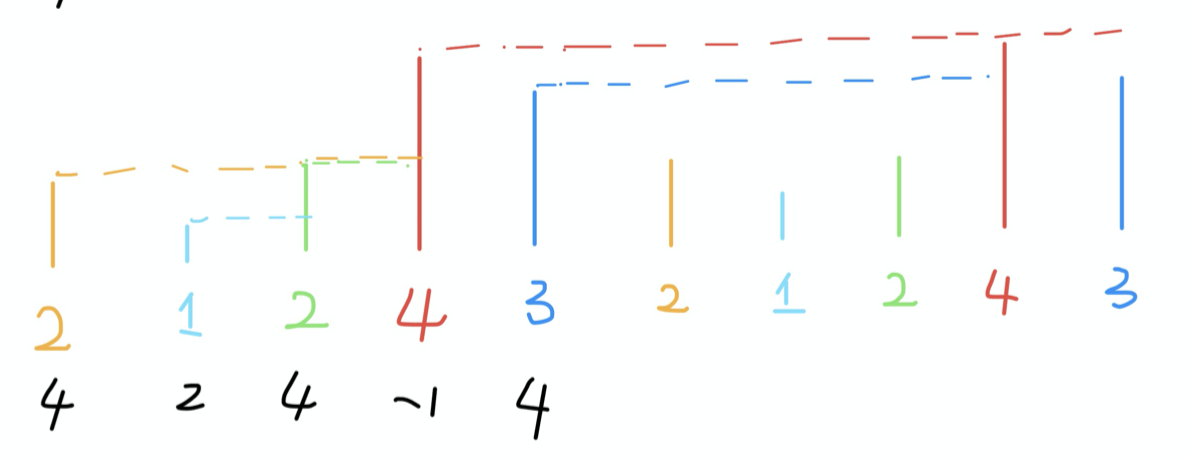
可以看出数组翻倍后,某个节点左边的点和右边的点都在该节点的后边。比如对于数组下标为2的值,其左边的值2和1,右边的值是4和3都在其后边
public int[] nextGreaterElements(int[] nums) {
int len=nums.length;
int res[]=new int[len];
Stack<Integer> stack=new Stack<>();
//从追加的后的数组的最后开始
for(int i=2*len-1;i>=0;i--)
{
while(!stack.isEmpty() && stack.peek()<=nums[i%len])
stack.pop();
if(i<len)
res[i]=stack.isEmpty()?-1:stack.peek();
stack.push(nums[i%len]);
}
return res;
}
这里的取余操作真的是太骚了。由于数组Double之后对应的值还是一样的,所以可以复用。这么骚的走位肯定是我借鉴大佬的解法

最后一道了,这也是我放弃了无数次的题目,每次看见都自动绕过。不过由于代码短小+思路精巧,面试出现 接雨水的频率还是挺高的
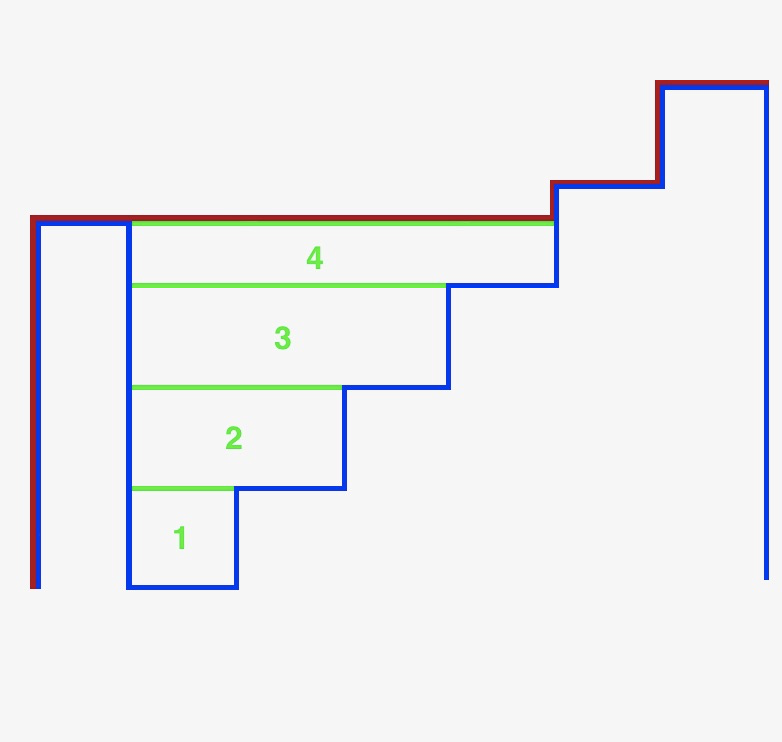
大家可以看下面这个图。当遍历到最右边的柱子的时,整个容器能盛雨水的的量是1+2+3+4的面积。对于1、2、3的面积而言,都是(二级阶梯之差)x(最右柱子到当前柱子之差)。4的面积是(最右柱子和当前柱子之差)x(最右柱子到当前柱子之差)
class Solution {
public int trap(int[] nums) {
Stack<Integer> stack=new Stack<>();
int res=0,last=0;
for(int i=nums.length-1;i>=0;i--)
{
while(!stack.isEmpty() && nums[stack.peek()]<=nums[i])
{
res+=(nums[stack.peek()]-last)*(stack.peek()-i-1);
last=nums[stack.peek()];
stack.pop();
}
//弹出的最后一个元素不再是和前面的差,而是和待插入元素的差
if(!stack.isEmpty())
res+=(nums[i]-last)*(stack.peek()-i-1);
//纪录的是下标方便计算二者的距离差
stack.push(i);
}
return res;
}
}