查找

根据给定的某个值，在查找表中确定一个其关键字等于给定值的数据元素（或记录）。

静态查找
只做查找操作，查找某个特定的元素是否在查找表中。

动态查找
在查找的过程中同时插入某个不存在的元素或者从查找表中删除某个特定的元素。

有序查找和无序查找
根据查找表的有序或者无序还分为有序查找和无序查找

无序查找

对于无序查找来说，因为查找表是无序的，只能进行一次遍历来确认能否查找成功。

a为查找表，n为查找表的长度，key为查找元素

int Sequential_Search(int *a,int n,int key){
    for (int i = 1; i <= n ; i++)
        if (a[i] == key)
            return i;
   
    return 0;
}

优化：上述代码需要遍历每个元素，然后进行对比，还有可以优化的空间。

int Sequential_Search_2(int *a,int n,int key){
    //空出a[0],设置a[0]=key,作为哨兵
    a[0] = key;
    int i = n;
    //从查找表的尾部开始查找，只需要进行i--和比较的操作，最终一定会返回一个i值，
    //如果i>0则表示找到key，如果i=0表示找到了哨兵，没有找到key
    //相比上面的代码，每次都缺少了判断i<n=的操作
    while(a[i]!=key) {
        i--;
    }
    return i;
}

顺序查找

上述无序查找的算法同样适用于顺序查找，但是对于顺序表来说，还有更优秀的查找算法。

1. 二分查找(折半查找)

比较简单，直接上代码了

int Binary_Search(int *a,int n,int key){
    
    int low,high,mid;
    //定义最低下标为记录首位
    low = 1;
    //定义最高下标为记录末位
    high = n;
    while (low <= high) {
        //折半计算
        mid = (low + high) /2;
        
        if (key < a[mid]) {
            //若key比a[mid] 小,则将最高下标调整到中位下标小一位;
            high = mid-1;
        }else if(key > a[mid]){
             //若key比a[mid] 大,则将最低下标调整到中位下标大一位;
            low = mid+1;
        }else
            //若相等则说明mid即为查找到的位置;
            return mid;
    }
    return 0;
}

因为需要不停的除2操作，折半查找的时间复杂度为O(lgn)。

折半查找的前提条件是需要有序表顺序存储，对于静态查找表，一次排序后不再变化，折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说，维护有序的排序会带来不小的工作量，那就不建议使用。——《大话数据结构》

2. 插值查找

插值查找是对折半查找的改进。在折半查找中

mid = (low+high)/2 = low + 1/2*(high-low)

如何对1/2进行改进呢？

mid = low + (key-a[low])/(a[high]-a[low])*(high-low)

分析上面的公式，(key-a[low])/(a[high]-a[low])求出的是key和a[low]的差值占这个a[high]和a[low]差值的比例，那么什么情况下这种比例可以代表key在查找表中的位置呢？很明显就是当查找表是均匀分布的情况下。

代码如下：

int Interpolation_Search(int *a,int n,int key){
    int low,high,mid;
    low = 1;
    high = n;
    
    while (low <= high) {
        
        //插值
        mid = low+ (high-low)*(key-a[low])/(a[high]-a[low]);
    
        if (key < a[mid]) {
            //若key比a[mid]插值小,则将最高下标调整到插值下标小一位;
            high = mid-1;
        }else if(key > a[mid]){
            //若key比a[mid]插值 大,则将最低下标调整到插值下标大一位;
            low = mid+1;
        }else
            //若相等则说明mid即为查找到的位置;
            return mid;
    }
    
    return 0;
}

时间复杂度为O(lgn)

3. 斐波那契查找

相比于折半查找和插值查找，斐波那契查找的mid值的获取变成了

mid = low + F[k-1] - 1

代码如下：

int F[100]; /* 斐波那契数列 */
int Fibonacci_Search(int *a,int n,int key){
    int low,high,mid,i,k;
    //最低下标为记录的首位;
    low = 1;
    //最高下标为记录的末位;
    high = n;
    k = 0;
    //1.计算n为斐波拉契数列的位置;
    while (n > F[k]-1) {
        k++;
    }
    //2.将数组a不满的位置补全值;
    for(i = n;i < F[k]-1;i++)
        a[i] = a[n];
    //3.
    while (low <= high) {
        //计算当前分隔的下标;
        mid = low+F[k-1]-1;
        if (key < a[mid]) {
            //若查找的记录小于当前分隔记录;
            //将最高下标调整到分隔下标mid-1处;
            high = mid-1;
            //斐波拉契数列下标减1位;
            k = k-1;
            
        }else if(key > a[mid]){
            //若查找的记录大于当前的分隔记录;
            //最低下标调整到分隔下标mid+1处
            low = mid+1;
            //斐波拉契数列下标减2位;
            k = k-2;
            
        }else{
            if (mid <= n) {
                //若相等则说明,mid即为查找的位置;
                return mid;
            }else
            {
                //若mid>n,说明是补全数值,返回n;
                return n;
            }
        }
    }
    return 0;
}

我们可以发现，在斐波那契查找中，我们将查找数组的个数更新为F[k]-1个，这是为什么呢？

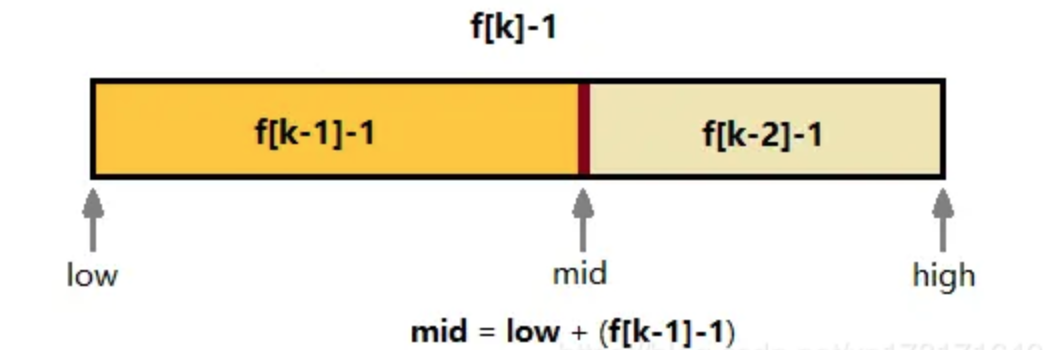
F[k-1]-1+1+F[k-2]-1 = F[k]-1 这种情况下假如mid和key不匹配，那我们的下一个区间也是符合F[k]-1的这种格式
假如选择F[k]，那么F[k]=F[k-1]+F[k-2]，缺少了mid点
假如选择F[k]+1，那么F[k]=F[k-1]+1+F[k-2]，mid点有了，但是下一次的区间又变成了F[k]这种。

二叉排序树/动态查找

定义

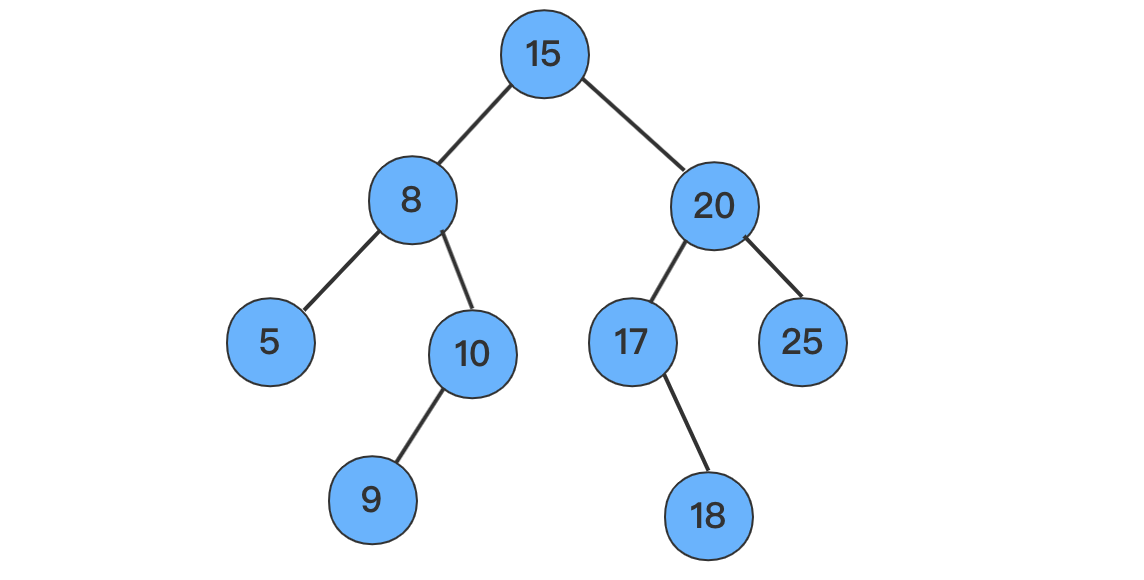
二叉排序树要么是一颗空树，要么具有以下特点：

二叉排序树中，如果其根结点有左子树，那么左子树上所有结点都小于根结点的值
二叉排序树中，如果其根结点有右子树，那么右子树上所有结点都大于根结点的值
二叉排序树的左右子树都是二叉排序树

//二叉树的二叉链表结点结构定义
//结点结构
typedef struct BiTNode
{
    //结点数据
    int data;
    //左右孩子指针
    struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

查找

对于一个排好序的二叉排序树进行查找，比较简单，假设根结点为T

根据二叉排序树的性质，如果key>T->data，到T的右子树中查找
如果key<T->data，到T的左子树有查找
如果相等，那么表示找到。

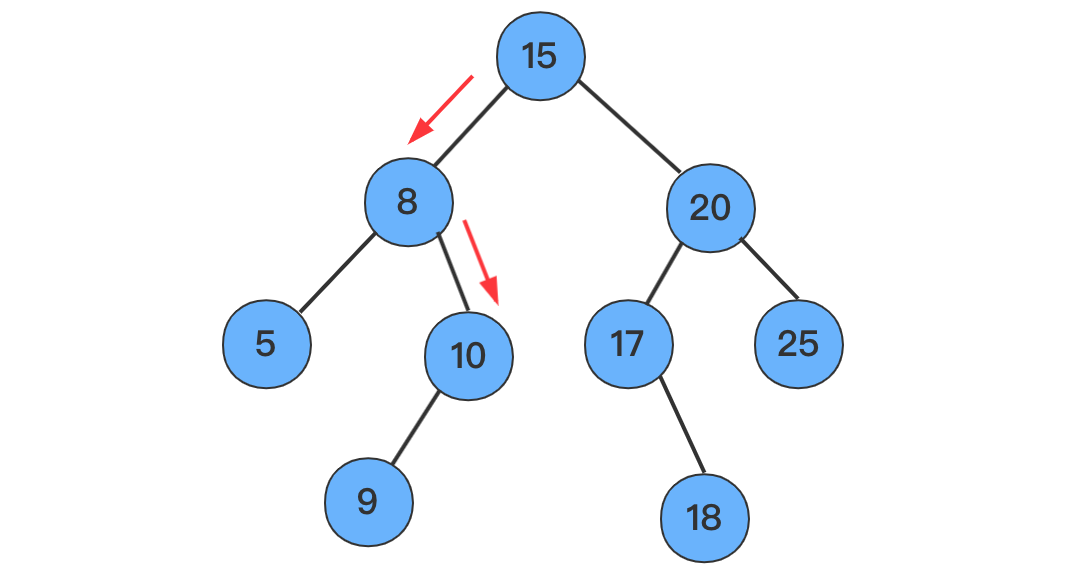
以10为例，
第一轮，15>10，到左子树中查找
第二轮，8<10，到右子树中查找
第三轮，10=10，查找成功

/// 查找二叉排序树
/// @param T 树的根结点
/// @param key 查找的key
/// @param f 当前节点T的双亲结点，默认为NULL
/// @param p 如果查找成功，p指向匹配的结点，否则指向查找路径的最后一个结点
Status SearchBST(BiTree T,int key,BiTree f, BiTree *p){
   
    if (!T)    /*  查找不成功 */
    {
        *p = f;
        return FALSE;
    }
    else if (key==T->data) /*  查找成功 */
    {
        *p = T;
        return TRUE;
    }
    else if (key<T->data)
        return SearchBST(T->lchild, key, T, p);  /*  在左子树中继续查找 */
    else
        return SearchBST(T->rchild, key, T, p);  /*  在右子树中继续查找 */
}

插入

先寻找当前树中是否存在要插入的结点，如果有，返回FALSE。
如果没有，通过上述的查找算法可以得到查找路径上的最后一个结点p。
如果p->data > key，则插入结点为p->lchild，否则为p->rchild。

/// 二叉树排序树的插入
/// @param T 根结点
/// @param key 要插入的key
Status InsertBST_1(BiTree *T, int key) {
    BiTree p;
    BiTree s;
    //先寻找树中是否已经存在对应的key
    if(!SearchBST(*T, key, NULL, &p)) {
        //创建要插入的结点
        s = (BiTree)malloc((sizeof(BiTNode)));
        s->data = key;
        s->lchild=s->rchild = NULL;
        //如果p为空，表示树为空。插入结点为根结点
        if(!p) {
            *T = s;
        }else if(p->data > key) {
            //如果key小于最后一个结点，则表示插入结点为最后一个结点的左子树
            p->lchild = s;
        }else {
            //如果key大于最后一个结点，则表示插入结点为最后一个结点的右子树
            p->rchild = s;
        }
    }
    //如果找到，返回false，确保二叉排序树中元素的唯一性
    return FALSE;
}

以插入19为例。

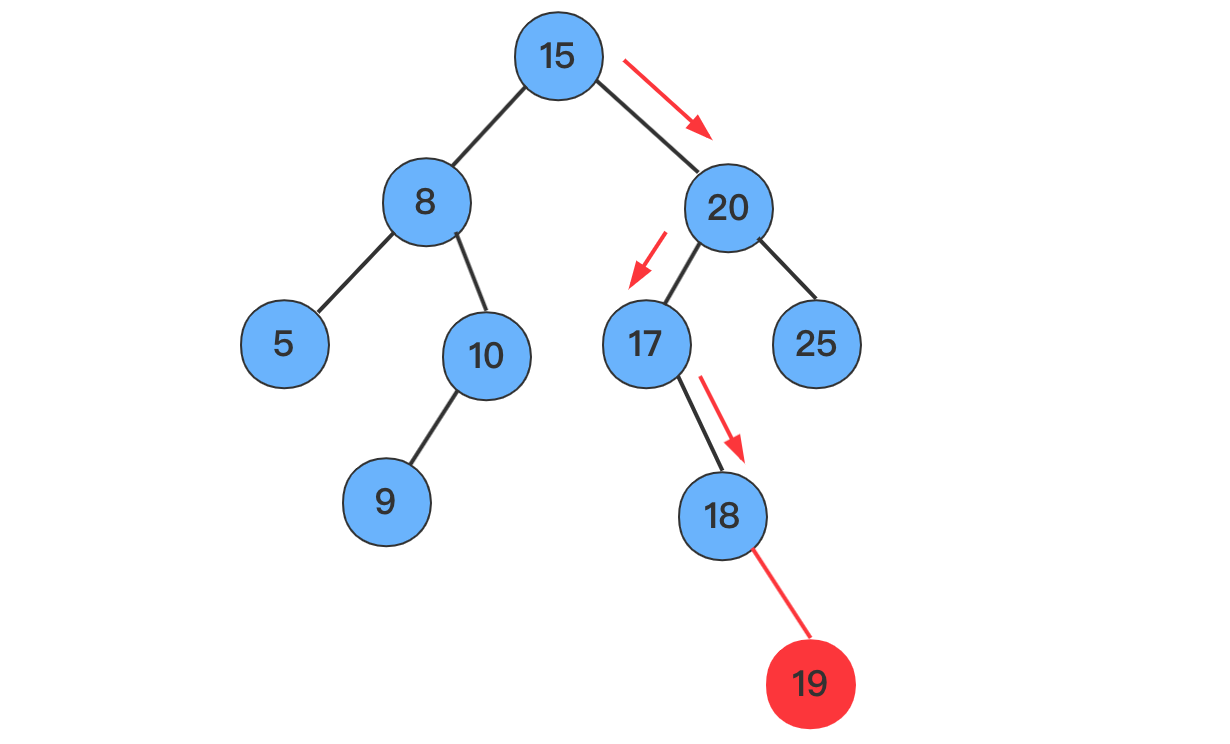
查找过程最终结束在结点18，因为18<19，因此新插入结点的18的右子树

删除

删除分为四种情况

如果左右子树都不存在，直接删除，例如删除18

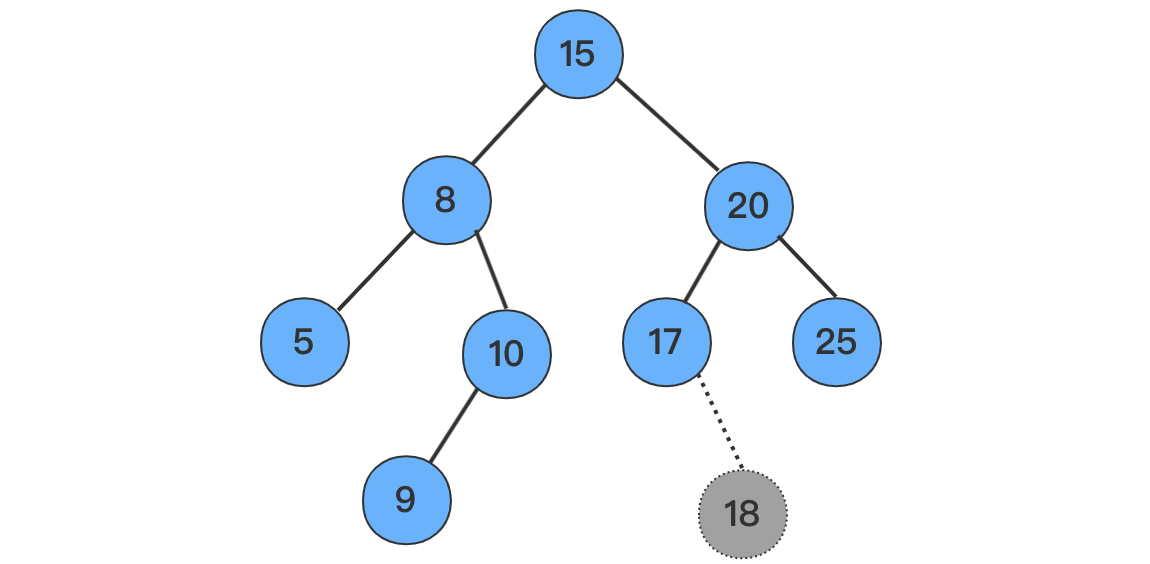
2. 如果右子树为空，左子树顶上，例如删除10

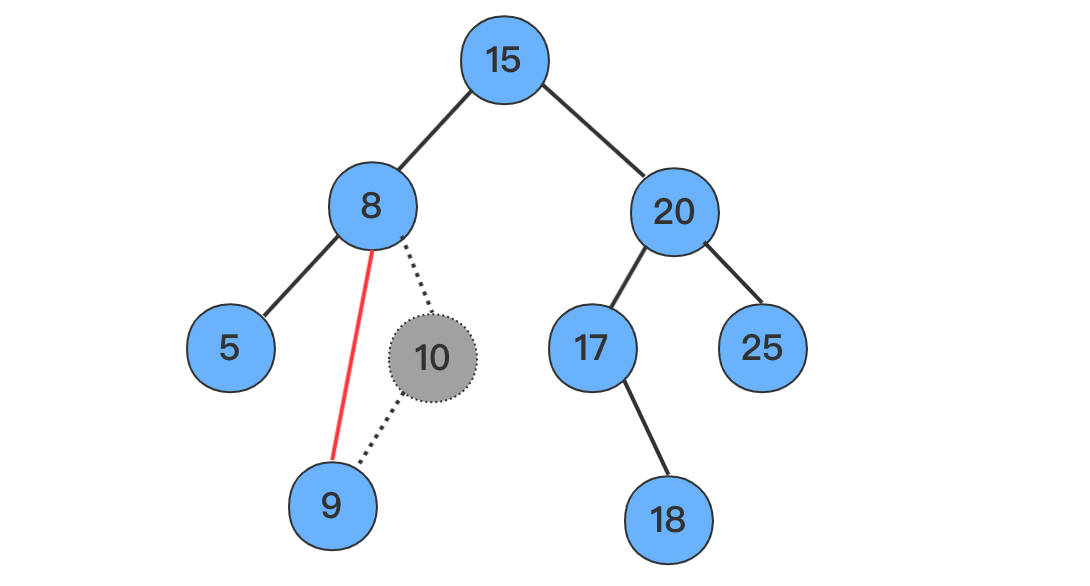
3. 如果左子树为空，右子树顶上，例如删除17

4. 如果左右子树都存在，有两种处理方式：
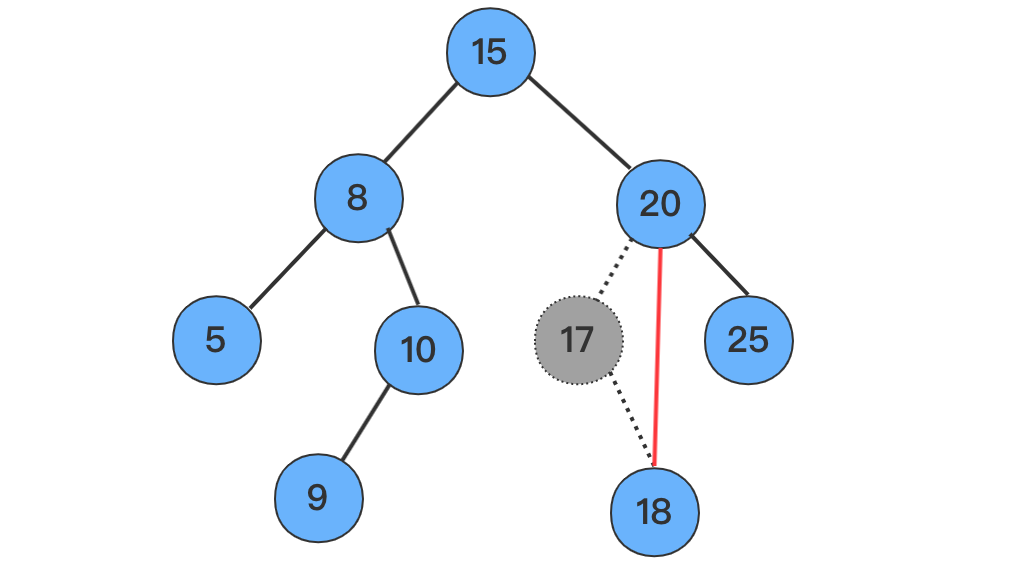
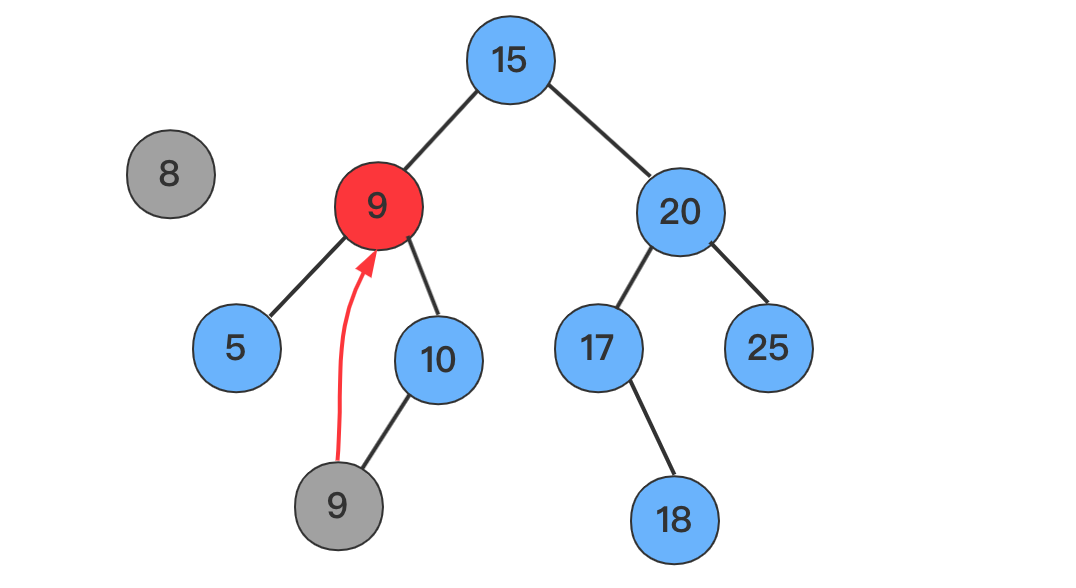
4.1 找到左子树的最右结点顶上，例如删除20

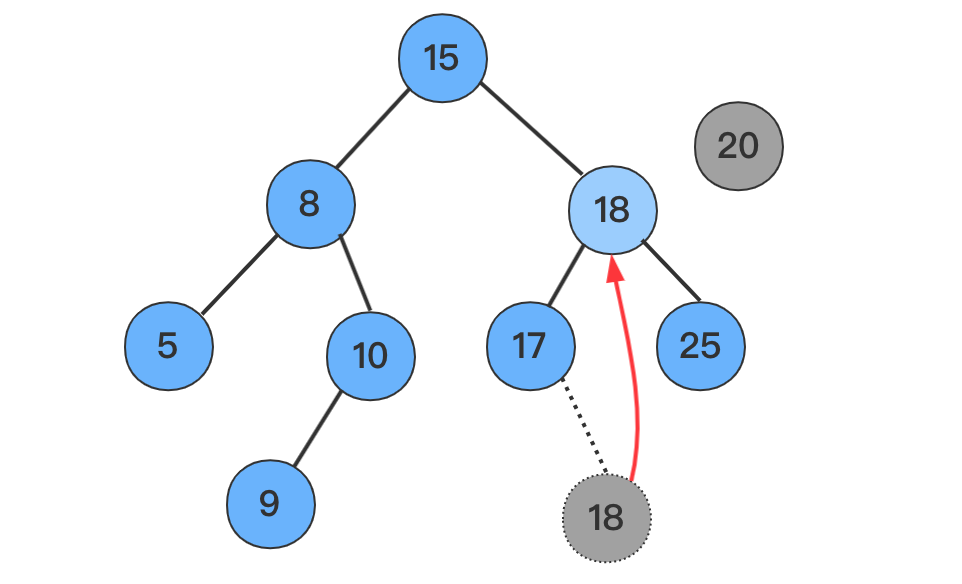
4.2 找到右子树的最左结点顶上，例如删除8

/// 要删除的结点
/// @param p 指向结点指针的指针，这样可以修改*p的值
Status Delete_1(BiTree *p){
    BiTree temp,s;
    if((*p)->lchild == NULL) {
        //如果待删除结点的左子树为空，右子树顶上
        temp = *p;
        *p = (*p)->rchild;
        free(temp);
    }else if((*p)->rchild == NULL) {
        //如果待删除结点的右子树为空，左子树顶上
        temp = *p;
        *p = (*p)->lchild;
        free(temp);
    }else {
        //如果待删除结点左右子树都存在，
        //此时有两种方案
        //1.拿左子树的最右结点顶上，因左子树的最右结点是左子树中最大的结点同时还小于右子树
        //2.拿右子树的最左结点顶上，因右子树的最左结点是右子树中最小的结点同时还大于左子树
        //我们选择第一种
        temp = *p;
        s = (*p)->lchild;
        while(s->rchild) {
            //寻找左子树的最右结点s，temp记录s的双亲结点
            temp = s;
            s = s->rchild;
        }
        //因为结点*p的左右子树都存在，我们直接拿要顶上的结点s的值来替换，然后删除s就行了。同时我们还要重连s的子树
        (*p)->data = s->data;
        if(temp != *p) {
            //表示左子树有最右结点，此时我们需要重连s的双亲结点的右子树与s的左子树
            temp->rchild = s->lchild;
        }else {
            //表示左子树无最右结点，此时我们需要重连s的双亲结点的左子树与s的左子树
            temp->lchild = s->lchild;
        }
        free(s);
        
    }
    return TRUE;
}

此外，我们需要先找到*p，才能进行删除。

Status DeleteBST_1(BiTree *T,int key) {
    //类似于查找
    if(!*T) {
        return FALSE;
    }else {
        if(key == (*T)->data) {
            return Delete(T);
        }else if(key < (*T)->data) {
            return DeleteBST_1(&((*T)->lchild), key);
        }else {
            return DeleteBST_1(&((*T)->rchild), key);
        }
    }
}

数据结构与算法-Day16-查找

查找