二叉排序树
二叉排序树(Binary Search Tree),(又:二叉搜索树,二叉查找树)它或者是一棵空树,或者是具有下列性质的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树。
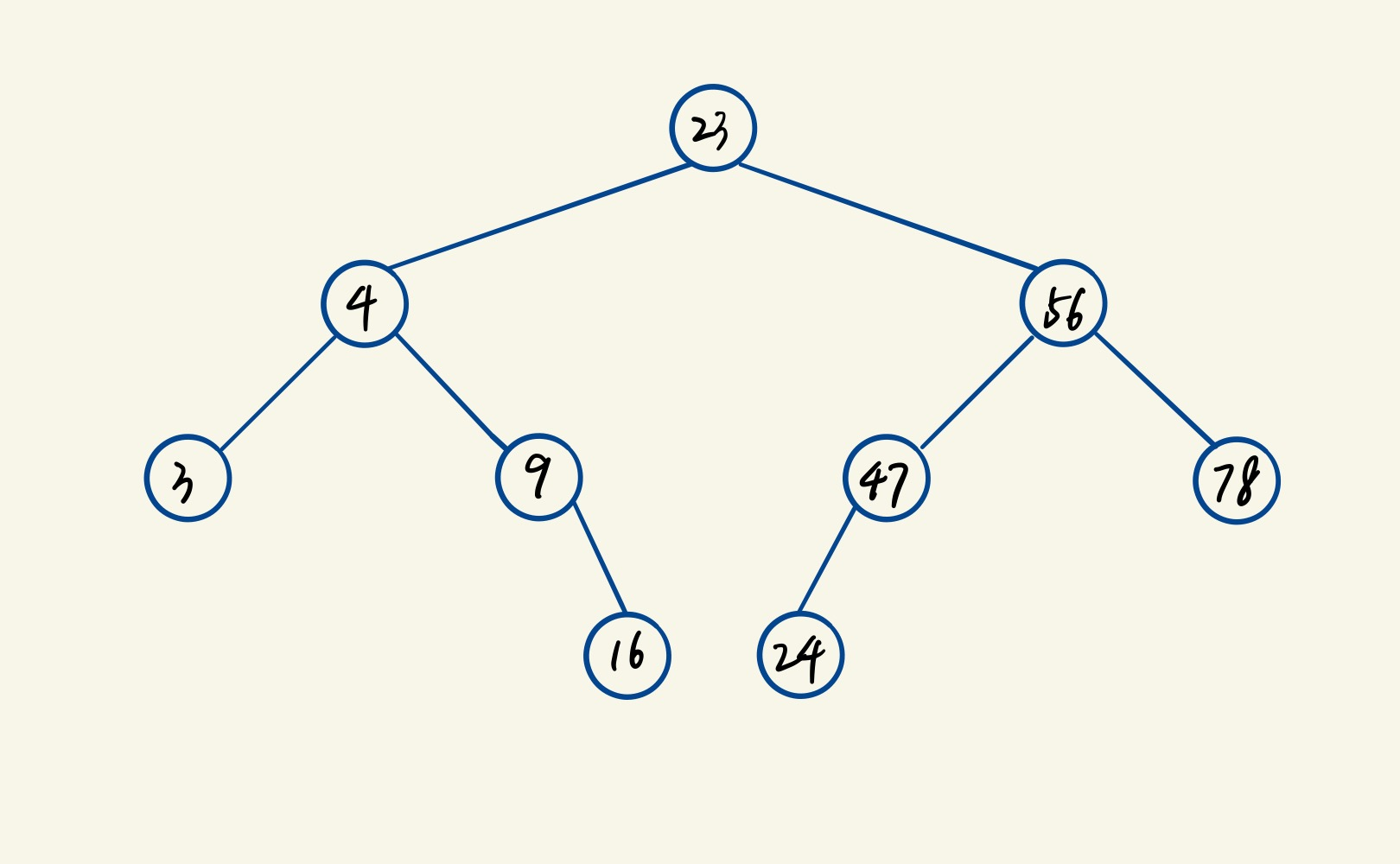
对二叉排序树的基本操作:
- 添加元素(insert)
- 获取最大元素(getMin)
- 获取最大元素(getMax)
- 查找某个元素是否存在于树中(find)
- 删除某个元素(remove)
- 输出树(toString)
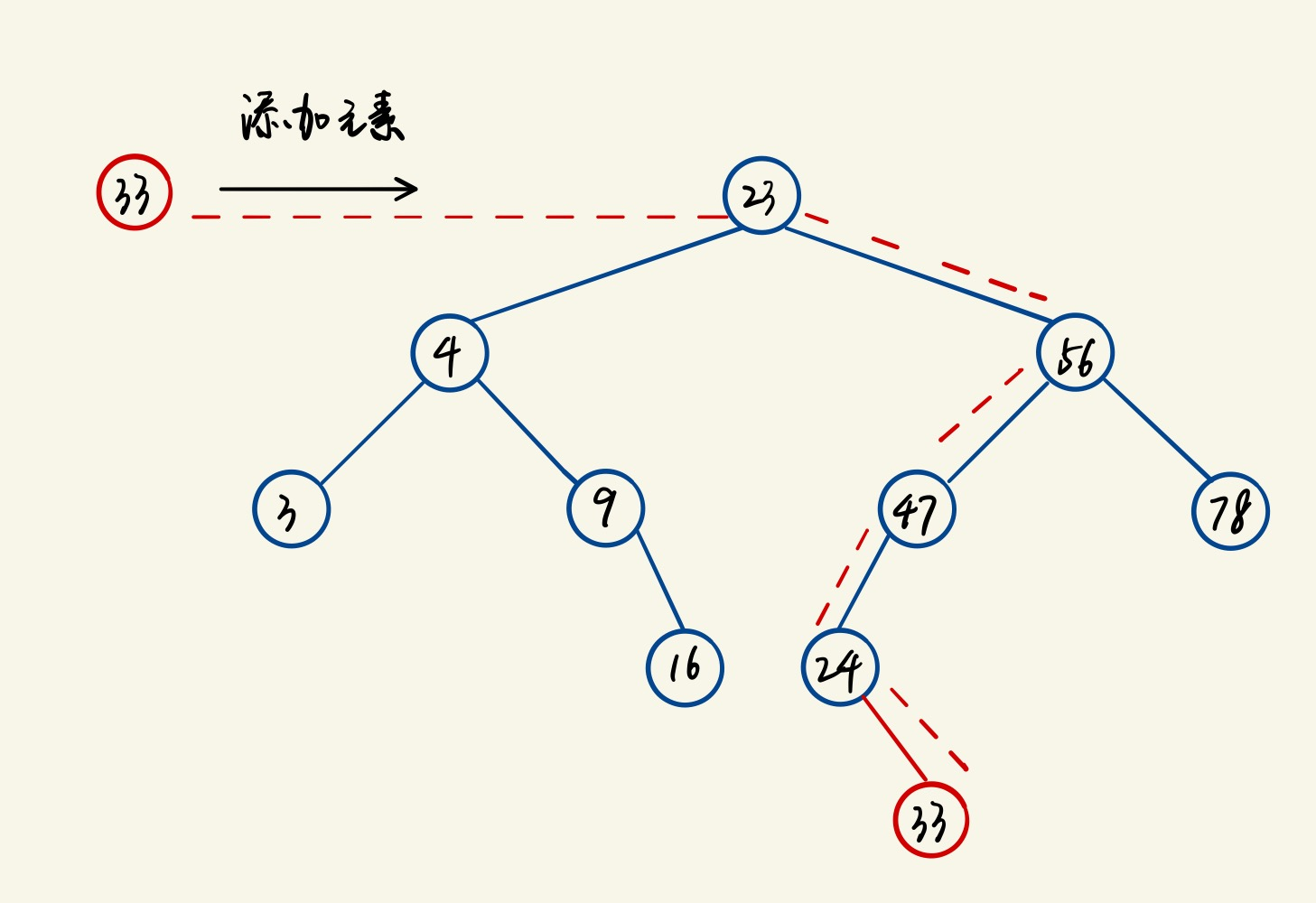
添加节点
通过insert方法向树添加节点。
- 首先检查BST是否有根节点,如果没有,说明是一个空树,该节点就是根节点。否则进入下一步。
- 设置根节点为当前节点。
- 若待插入节点的数据小于当前节点,则设当前节点的左节点为新的当前节点。否则进入第5步。
- 若当前节点的左节点为null,就将新的节点插入这个位置,退出循环;反之,继续执行下一次循环。
- 若待插入节点的数据大于当前节点,则设当前节点的右节点为新的当前节点。
- 若当前节点的右节点为null,就将新的节点插入这个位置,退出循环;反之,继续执行下一次循环。
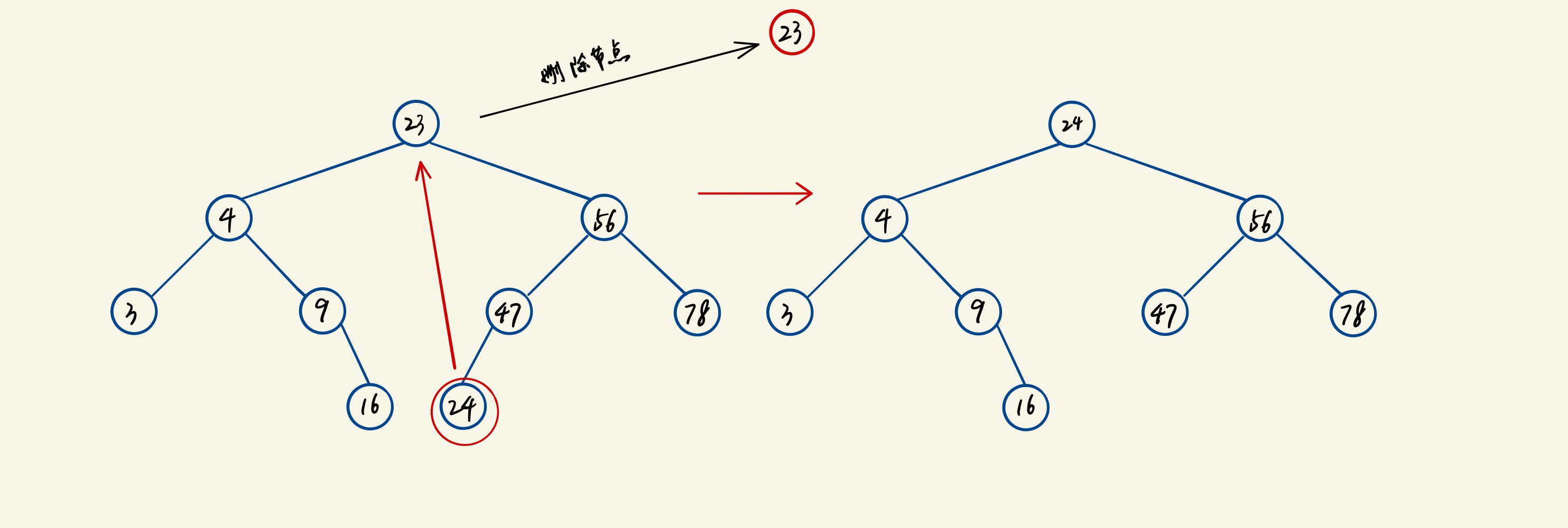
删除节点
通过remove方法删除节点。
- 首先设置根节点为当前节点。
- 判断当前节点是否包含待删除的数据,如果包含,则删除该节点;否则比较当前节点上的数据和待删除的数据。
- 如果待删除的数据小于当前节点的数据,则移动至当前节点的左子节点继续比较;如果待删除数据大于当前节点的数据,则移动至当前节点的右子节点继续比较。
删除节点有三种情况:
- 待删除节点是叶子节点。只需要将从父节点指向它的链接指向null。
- 待删除节点只包含一个子节点。只需要将从父节点指向它的链接指向指向待删除节点的子节点。
- 待删除节点包含两个子节点。正确的做法有两种:要么查找待删除节点左子树上的最大值,要么查找其右子树上的最小值。本文的示例代码选择的是后一种方式。我们需要一个查找子树上最小值的方法
getRightChildSmallest(),会用它找到的最小值创建一个临时节点。将临时节点上的值复制到待删除节点,然后再删除子树上的临时节点。
/*
* 节点类
* Node对象存储数据,保存和其他节点的链接(left和right),show()方法用来显示保存在节点中的数据。
*/
class Node{
constructor(data,left,right){
this.data = data;
this.left = left;
this.right = right;
}
show(){
return this.data;
}
}
class BST{
constructor(){
this.root = null;
}
insert(data){
let node = new Node(data,null,null);
if(this.root === null){
this.root = node;
}else{
let current = this.root, parent = null;
while(true){
parent = current;
if(data < current.data){
current = current.left;
if(current === null){
parent.left = node;
break;
}
}else{
current = current.right;
if(current === null){
parent.right = node;
break;
}
}
}
}
}
//中序遍历
toString(node){
node = node===undefined ? this.root : node;
let str = "";
if(node !== null){
str = str + this.toString(node.left);
str = str + node.show()+" ";
str = str + this.toString(node.right);
}
return str;
}
getMin(){
let current = this.root;
while(current.left !== null ){
current = current.left;
}
return current.show();
}
getMax(){
let current = this.root;
while(current.right !== null ){
current = current.right;
}
return current.show();
}
find(data){
let current = this.root;
while(current !== null){
if(current.data === data){
return true;
}else if(current.data < data){
current = current.right;
}else{
current = current.left;
}
}
return false;
}
getRightChildSmallest(node){
let current = node.right;
while(current.left !== null){
current = current.left;
}
return current;
}
remove(data){
this.removeTmp(this.root,data);
}
removeTmp(node, data){
if(node === null){
return null;
}
if(node.data === data){
if(node.left === null && node.right === null){ //判断是否是叶子节点
return null;
}else if(node.left === null){//判断是否只有右子节点
return node.right;
}else if(node.right === null){//判断是否只有左子节点
return node.left;
}
//存在两个子节点,查找其右子树上的最小值
let tmpNode = this.getRightChildSmallest(node);
node.data = tmpNode.data;
node.right = this.removeTmp(node.right,tmpNode.data); //再删除子树上的临时节点
return node;
}else if(node.data < data){
node.right = this.removeTmp(node.right,data);
return node;
}else{
node.left = this.removeTmp(node.left,data);
return node;
}
}
}
let bst = new BST();
bst.insert(23);
bst.insert(4);
bst.insert(78);
bst.insert(3);
bst.insert(9);
bst.insert(16);
bst.insert(47);
bst.insert(24);
console.log(bst.toString()); //3 4 9 16 23 24 47 78
bst.remove(23)
console.log(bst.toString()); //3 4 9 16 24 47 78
应用
使用二叉排序树对数组进行排序。
let arr = [12,97,58,39,27,19,69,47,36];
let tmp = new BST();
for(let i = 0; i < arr.length; i++){
tmp.insert(arr[i]);
}
console.log(tmp.toString()); //12 19 27 36 39 47 58 69 97