这篇博客写给我的爱豆,最近她在面试,希望她早早拿到offer。我试着分析下。
绪论
众所周知,排序算法分为很多种。分别有冒泡排序、基数排序、插入排序、归并排序、快速排序、选择排序、希尔排序、堆排序等,接下就每种排序算法进行详细介绍分析。
冒泡排序
冒泡排序是最简单的排序算法,比较容易被想到,加上时间复杂度较高O(),所以在面试中被问到的概率不大。动图效果如下:
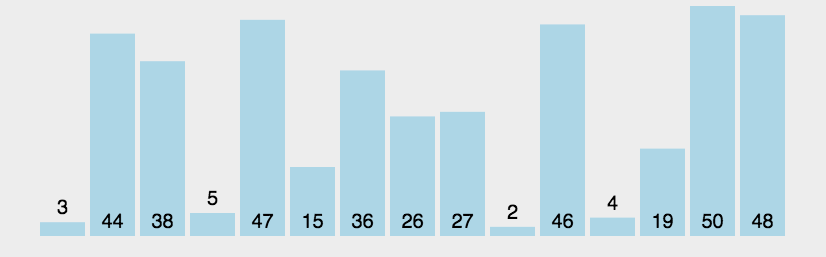
public static void bubbleSort(int[] a){
int length = a.length;
int temp;
for(int i=0;i<length;i++){
for(int j=0;j<length-i-1;j++){
if(a[j]>a[j+1]){
temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
}
}
}
}
由此可见冒泡排序比较直观。
基数排序
基数排序是先按照元素的低位进行排序,收集后,再按照高位进行排序,最后得到的数组顺序就是排序后的数组顺序,因此相对来说时间复杂度是O(),其中n是元素总数,l是最大数的位数。
算法思想:
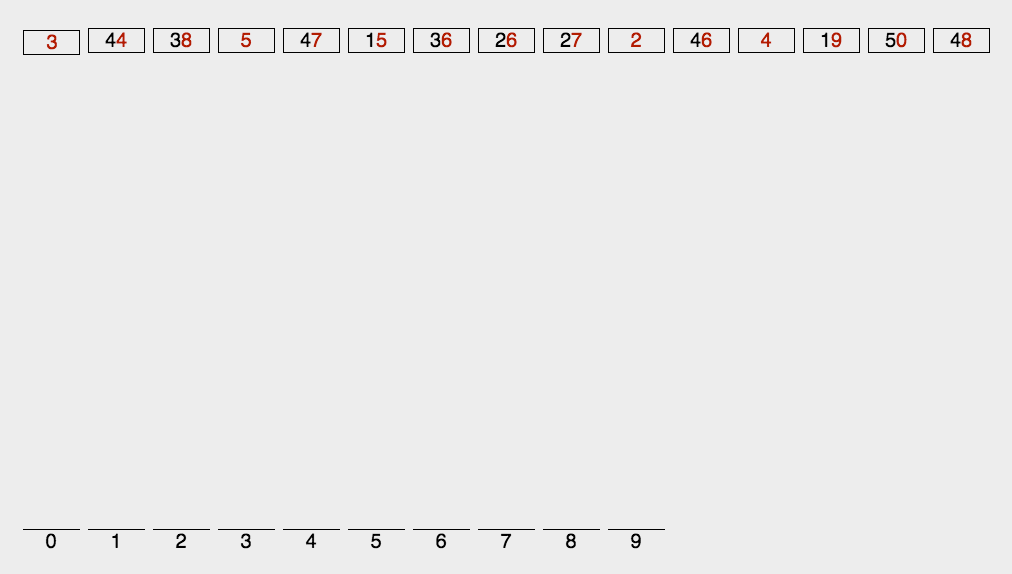
public static void sort(int[] array) {
//首先确定排序的趟数;
int max = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
}
int time = 0;
//判断位数;
while (max > 0) {
max /= 10;
time++;
}
//建立10个队列;
List<ArrayList> queue = new ArrayList<ArrayList>();
for (int i = 0; i < 10; i++) {
ArrayList<Integer> queue1 = new ArrayList<Integer>();
queue.add(queue1);
}
//进行time次分配和收集;
for (int i = 0; i < time; i++) {
//分配数组元素;
for (int j = 0; j < array.length; j++) {
//得到数字的第time+1位数;
int x = array[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
ArrayList<Integer> queue2 = queue.get(x);
queue2.add(array[j]);
queue.set(x, queue2);
}
int count = 0;//元素计数器;
//收集队列元素;
for (int k = 0; k < 10; k++) {
while (queue.get(k).size() > 0) {
ArrayList<Integer> queue3 = queue.get(k);
array[count] = queue3.get(0);
queue3.remove(0);
count++;
}
}
}
}
插入排序
插入排序主要是构建有序序列,对未排序数据,从已排序序列从后向前扫描,插入,在任何一时刻,新序列都是有序的。平均时间度O(),最坏时间复杂度也是O(
)。
算法思想:从第一个元素开始,该元素可以认为已经被排序; 取出下一个元素,在已经排序的元素序列中从后向前扫描; 如果该元素(已排序)大于新元素,将该元素移到下一位置;一直进行重复,直到最后元素。
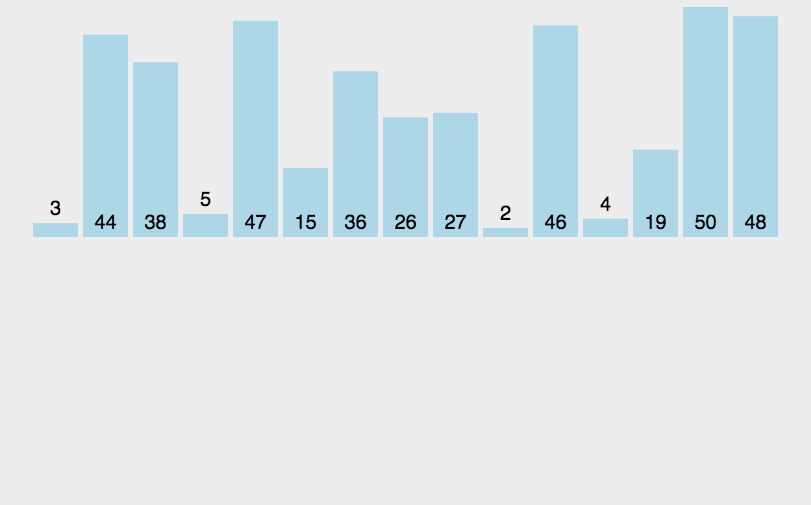
public static void insertSort(int[] a){
int length = a.length;
int insertNum;
for(int i=1;i<length;i++){//插入的次数
insertNum = a[i];//要插入的数
int j = i-1;//已经排序好的序列元素的个数
while(j>=0 && a[j]>insertNum){//序列从后到前循环,将大于insertNum的数向后一位
a[j+1] = a[j];//元素移动一位
j--;
}
a[j+1] = insertNum;//将需要插入的数放在要插入的位置。
}
}
归并排序
归并排序是采用分治法进行排序。将有序序列的子序列合并,得到完全有序的序列。平均时间复杂度为O() ,最坏时间复杂度也是O(
)
算法思想:
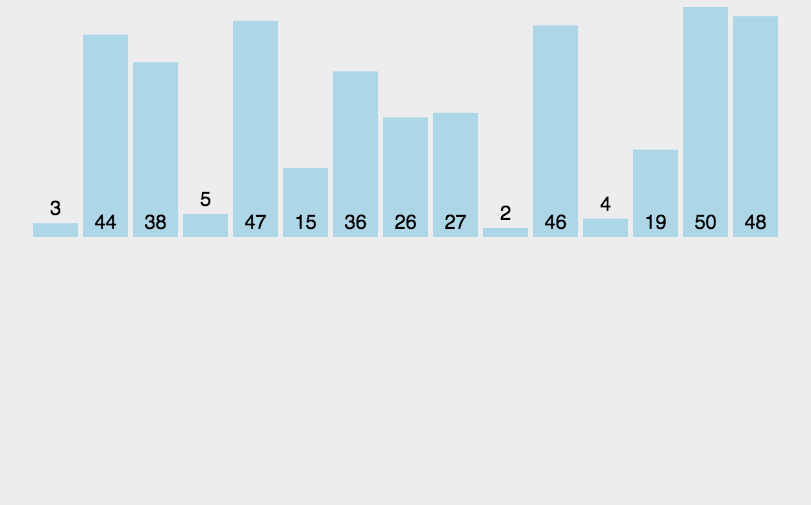
public static void mergeSort(int[] numbers, int left, int right) {
int t = 1;// 每组元素个数
int size = right - left + 1;
while (t < size) {
int s = t;// 本次循环每组元素个数
t = 2 * s;
int i = left;
while (i + (t - 1) < size) {
merge(numbers, i, i + (s - 1), i + (t - 1));
i += t;
}
if (i + (s - 1) < right){
merge(numbers, i, i + (s - 1), right);
}
}
}
private static void merge(int[] data, int p, int q, int r) {
int[] B = new int[data.length];
int s = p;
int t = q + 1;
int k = p;
while (s <= q && t <= r) {
if (data[s] <= data[t]) {
B[k] = data[s];
s++;
} else {
B[k] = data[t];
t++;
}
k++;
}
if (s == q + 1){
B[k++] = data[t++];
}else{
B[k++] = data[s++];
}
for (int i = p; i <= r; i++){
data[i] = B[i];
}
}
快速排序
快速排序也是采取了分治法的思想,将待排序列分隔成独立的两部分,一部分的关键字均比另一部分少,然后分别对两部分记录排序,最后达到整个序列有序。平均时间复杂度:O(),最坏时间复杂度O(
)

public static void quickSort(int[] numbers,int start,int end){
if(start<end){
int base = numbers[start];//选定基准(第一个数值作为基准)
int temp;//记录临时中间值
int i= start,j = end;
do{
while((numbers[i]<base)&& (i<end)){
i++;
}
while((numbers[j]>base)&& (j>start)){
j--;
}
if(i<=j){
temp = numbers[i];
numbers[i] = numbers[j];
numbers[j] = temp;
i++;
j--;
}
}while (i<=j);
if(start<j){
quickSort(numbers,start,j);
}
if(end>i){
quickSort(numbers,i,end);
}
}
}
选择排序
选择排序相对比较直观,从未排序序列中找到最小(大)元素,放到序列起始位,然后在剩下中继续找,依次类推。平均时间复杂度O(),最坏时间复杂度O(
)
算法思想:
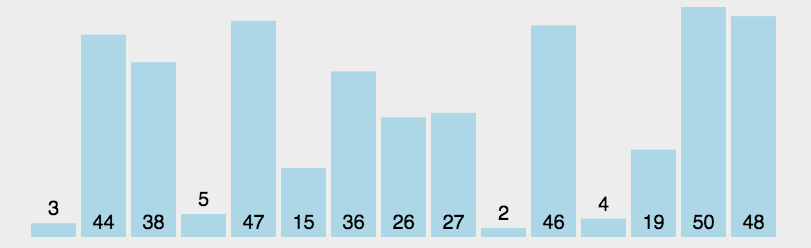
java代码:
public static void selectSort(int[] a){
int length = a.length;
for(int i=0;i<length;i++){
int key = a[i];
int position = i;
for(int j=i+1;j<length;j++) {
if (a[j] < key) {
key = a[j];
position = j;
}
}
a[position] = a[i];
a[i] = key;
}
}
希尔排序
最初被提出为了打破排序时间复杂度为O()。平均时间复杂度为O(
),但最坏也会达到O(
)。
算法思想: 将待排序序列的拷贝序列分成若干个子序列分别进行直接插入排序。不断缩减步长进行循环对比大小,如果符合排序大小,就下一个元素,不符合就交换元素。
直接看图和代码比较直观,这个我说的比较累赘。
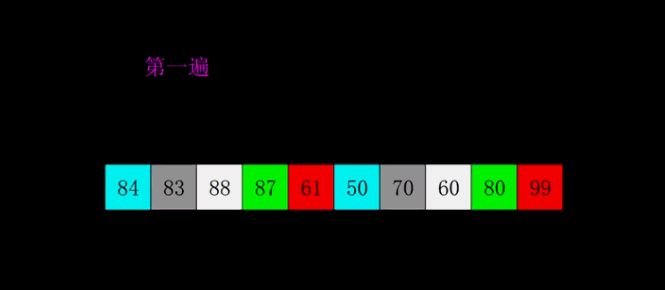
public static void shelSort(int[] a){
int d = a.length;
while(d!=0){
d = d/2;
for(int x = 0;x<d;x++){//分的组数
for(int i=x+d;i<a.length;i+=d){//组中的元素,从第二个数开始,直接插入排序
int j = i-d;//j为有序序列最后一位的位数
int temp = a[i];//要插入的元素
for(;j>=0&&temp <a[j];j-=d){//从后往前遍历
a[j+d] = a[j];//想后移位
}
a[j+d] = temp;
}
}
}
}
堆排序(我放到最后,你了解完数据结构再来学习这种算法)
堆排序是利用数据结构而进行设计的一种排序算法。堆近似二叉树。在堆中一般子结点的值总是小于(或者大于,按照排序要求设置)父结点。平均时间复杂度:O()
算法思想:
构建大顶推或者小顶堆,然后将最顶上元素与堆最后元素进行交换,然后排除最顶上元素,将剩下元素再进行大顶堆或者小顶堆的构建。最后再不断循环排除。说起来有点绕口,直接上图。

public static void heapSort(int[] a){
System.out.println("开始排序");
int arrayLength=a.length;
//循环建堆
for(int i=0;i<arrayLength-1;i++){
//建堆
buildMaxHeap(a,arrayLength-1-i);
//交换堆顶和最后一个元素
swap(a,0,arrayLength-1-i);
}
}
private static void swap(int[] data, int i, int j) {
// TODO Auto-generated method stub
int tmp=data[i];
data[i]=data[j];
data[j]=tmp;
}
//对data数组从0到lastIndex建大顶堆
private static void buildMaxHeap(int[] data, int lastIndex) {
//从lastIndex处节点(最后一个节点)的父节点开始
for(int i=(lastIndex-1)/2;i>=0;i--){
//k保存正在判断的节点
int k=i;
//如果当前k节点的子节点存在
while(k*2+1<=lastIndex){
//k节点的左子节点的索引
int biggerIndex=2*k+1;
//如果biggerIndex小于lastIndex,即biggerIndex+1代表的k节点的右子节点存在
if(biggerIndex<lastIndex){
//若果右子节点的值较大
if(data[biggerIndex]<data[biggerIndex+1]){
//biggerIndex总是记录较大子节点的索引
biggerIndex++;
}
}
//如果k节点的值小于其较大的子节点的值
if(data[k]<data[biggerIndex]){
//交换他们
swap(data,k,biggerIndex);
//将biggerIndex赋予k,开始while循环的下一次循环,重新保证k节点的值大于其左右子节点的值
k=biggerIndex;
}else{
break;
}
}
}
}
写了一下午,祝你学的开心!!!如有不正确的,请评论指正,会立即修改,谢谢。