一、概念
-
路径:从一个结点到另一个结点所经过的所有结点,被我们称为两个结点之间的路径。
-
路径长度:从一个结点到另一个结点所经过的“边”的数量,被我们称为两个结点之间的路径长度。
-
树的路径长度:从根结点到每一个结点的路径长度之和。
-
结点的带权路径长度:树的每一个结点,都可以拥有自己的“权重”(Weight),权重在不同的算法当中可以起到不同的作用。结点的带权路径长度,是指树的根结点到该结点的路径长度,和该结点权重的乘积。
-
树的带权路径长度:所有叶子结点的带权路径长度之和,被称为树的带权路径长度,也被简称为WPL。
哈夫曼树
假设学生成绩分布图
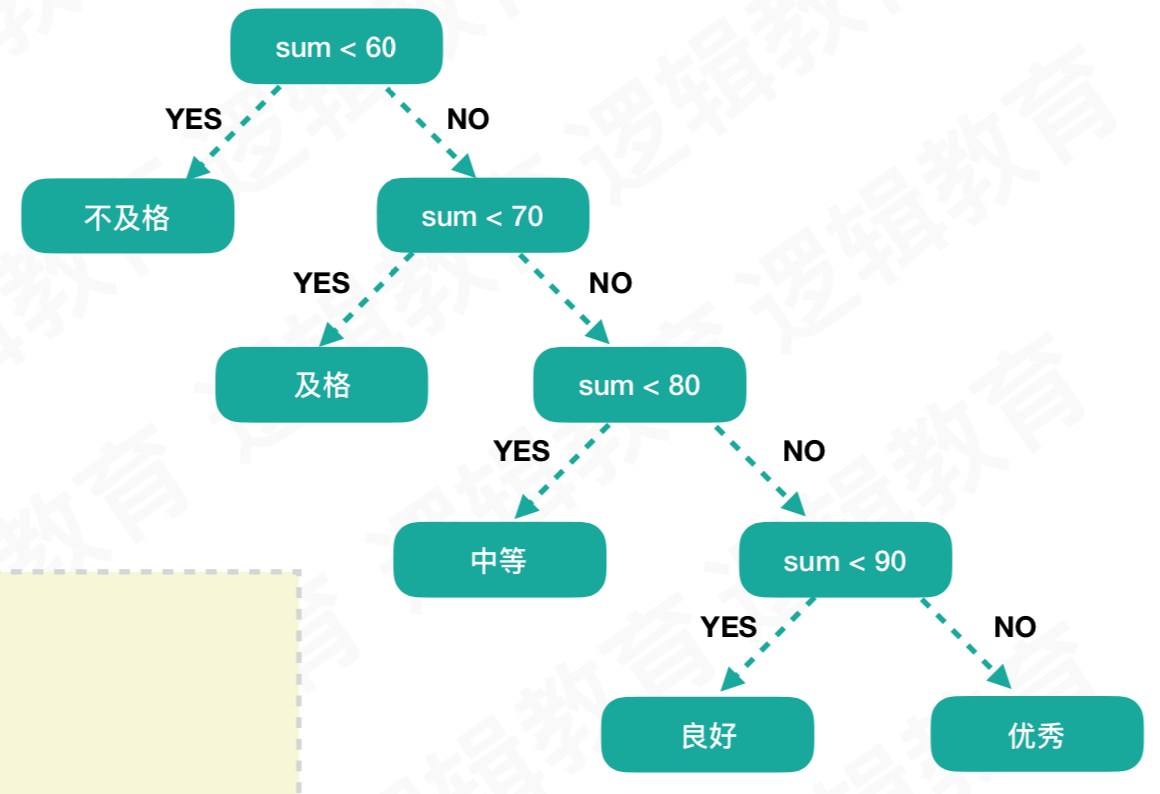
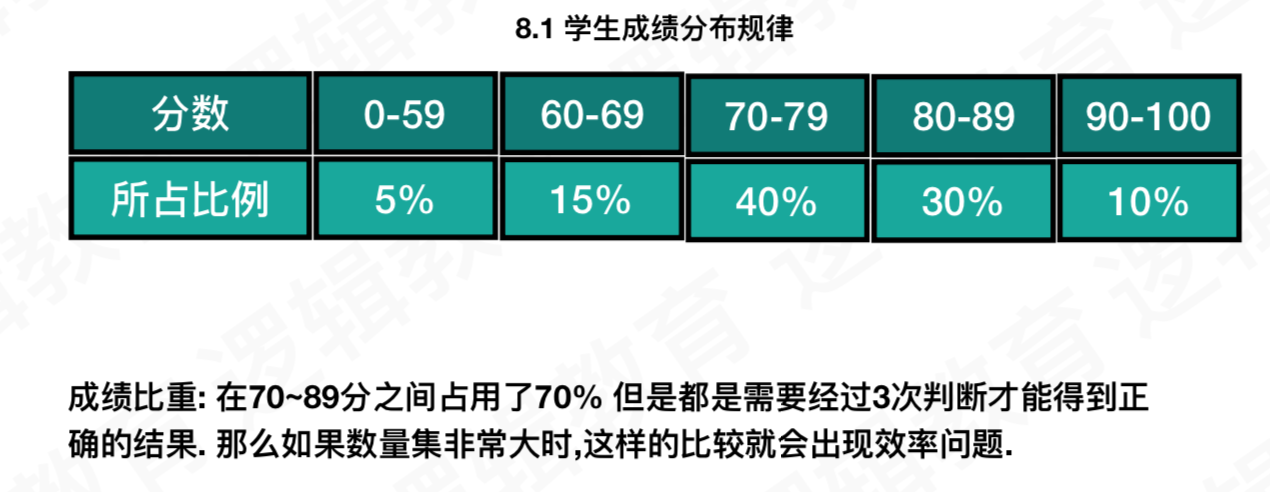
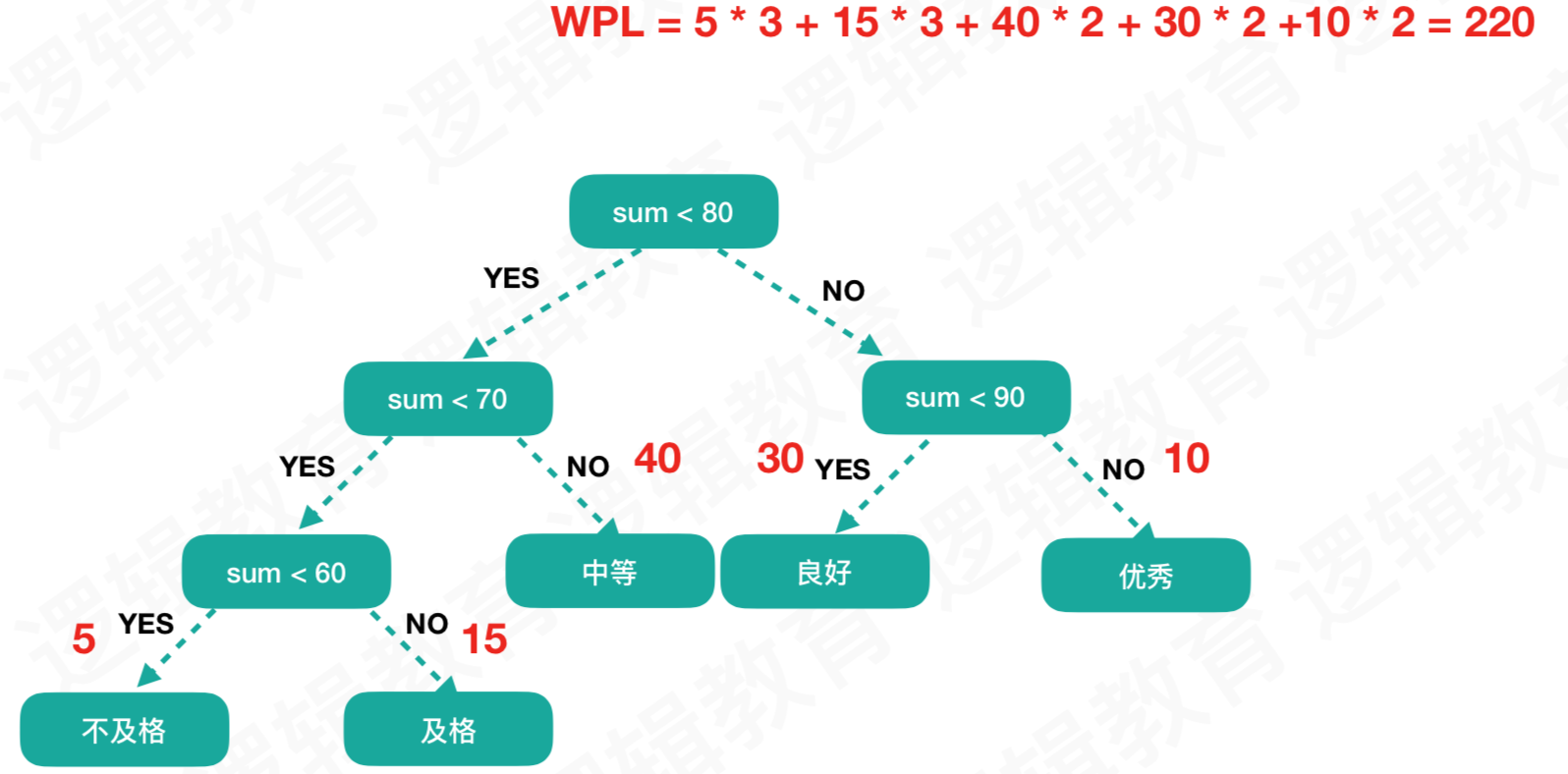
如果是数量集很大的情况下,这样的比较会出现很严重的效率问题。因为人数比重比较多的是70-79分,想要得到“中等”这个结果,需要经过3次判断。其实根据所占比例(权重),可以生成一个更优质的二叉树结构。
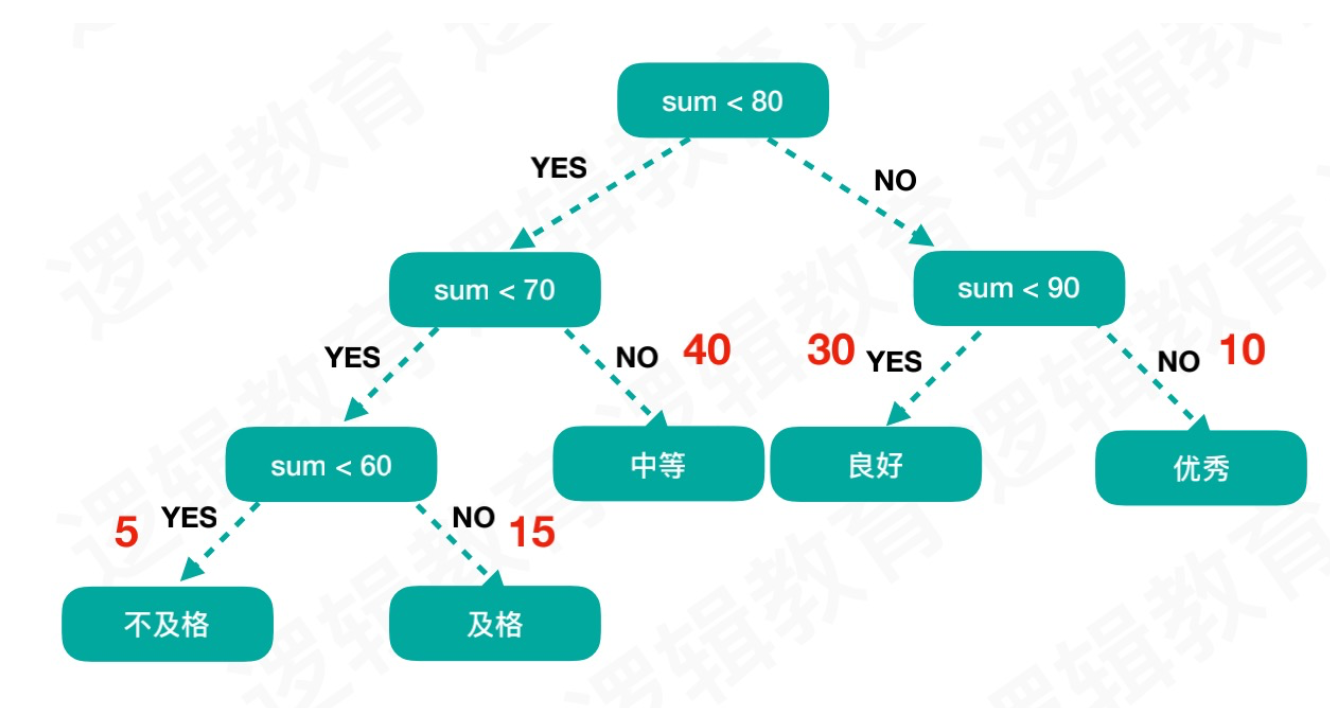
通常我们使用WPL(树的带权路径长度)来计算优质性,权重值就是学生所占比例 x 树到指定节点的路径
- 优化前:1x5 + 2x15 + 3x40 + 4x30 + 4x10 = 315
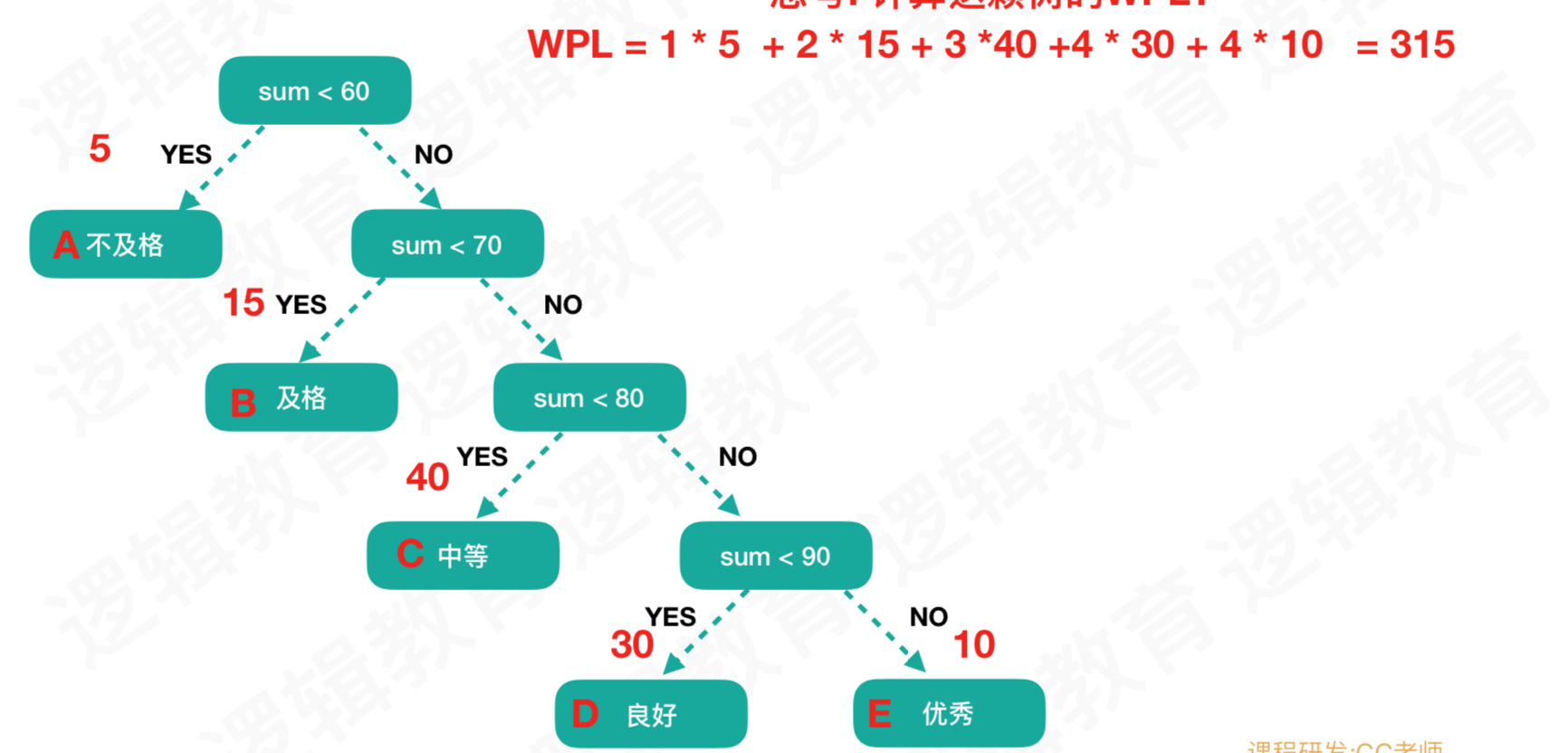
- 优化后:5x3 + 15x3 + 40x2 + 30x2 + 10x2 = 220
构建过程
假设我们有A:5、B:15、C:40、D:30、E:10,的数据,怎么得到WPL最小的数呢?
首先我们根据权重的大小进行排序:

先将最小的两个作为子节点,得到一个新的节点,这个节点的权重是叶子节点权重之和,N1:15
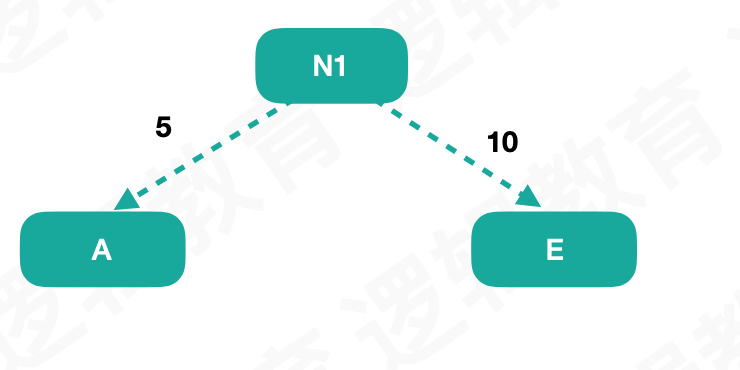
然后得到了新的数据:N1:15、B:15、D:30、C:40
再将最小的两个作为子节点,得到一个新节点:
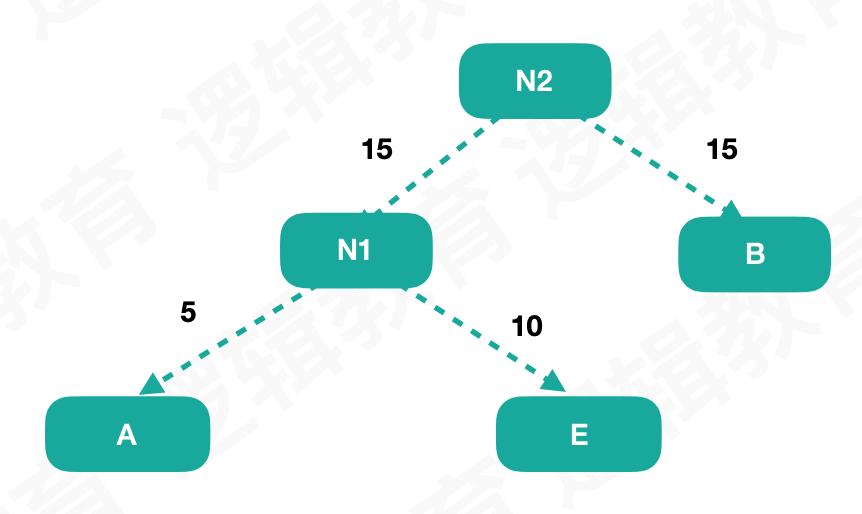
然后按照这样,每次取出最小的权重作为子节点,生成一个新节点,知道所有的节点都取到:
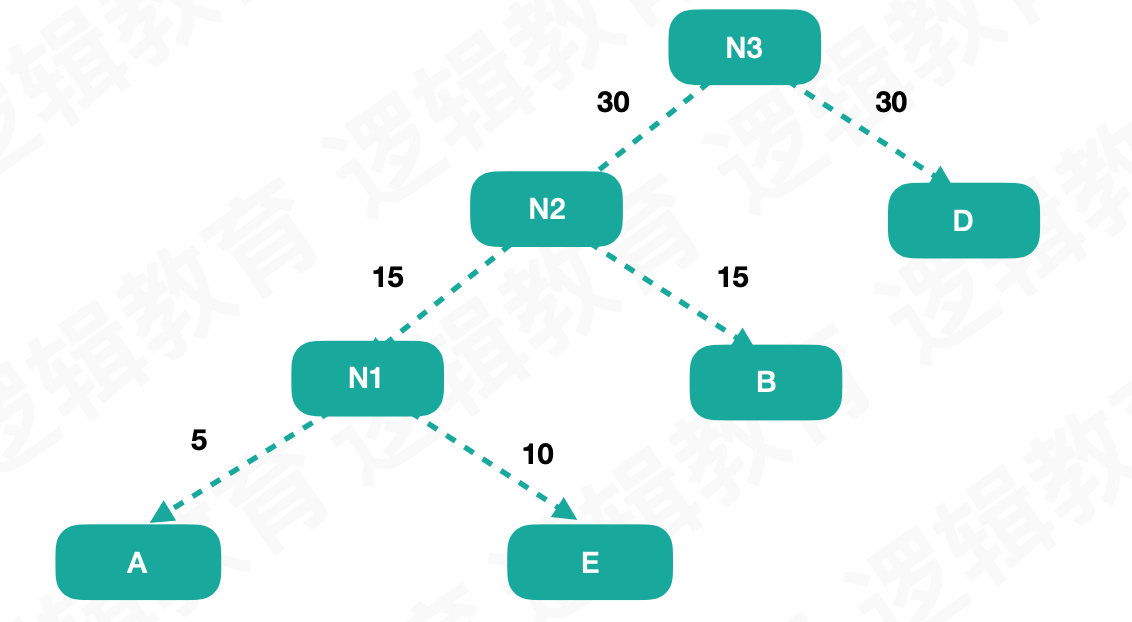
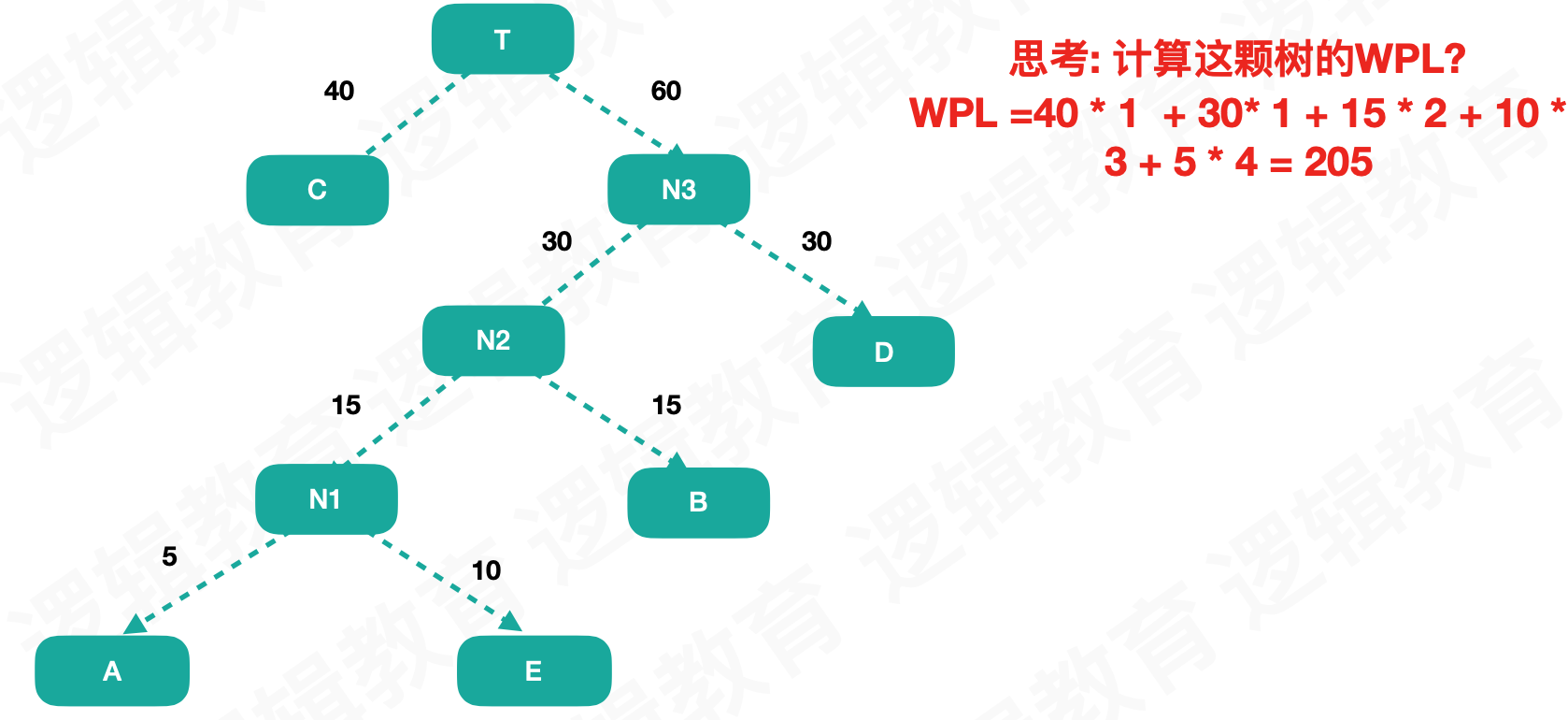
这样我们就得到了一个WPL最小的树,这种树就叫做哈夫曼树
哈夫曼编码的使用
正常我们传输数据最终形式都0和1的组合,假如我们把abcd按照正常数据排列就是

- 字母都是通过三位的二进制表示,后面数字是该字母在传输数据中出现的次数,这样我们传输数据时候每个字母都是需要三位0或者1来表示
- 假如我们通过编码让不同的组合表示字母,这样就会减少0和1的位数,从而减少数据的传输量
- 这种方式用到文件压缩中
我们通过哈夫曼编码来进行转换:
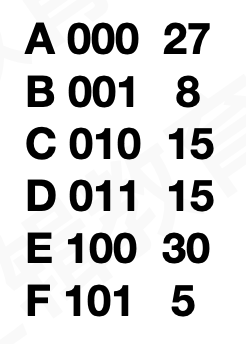
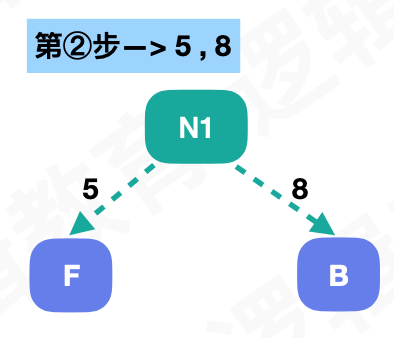
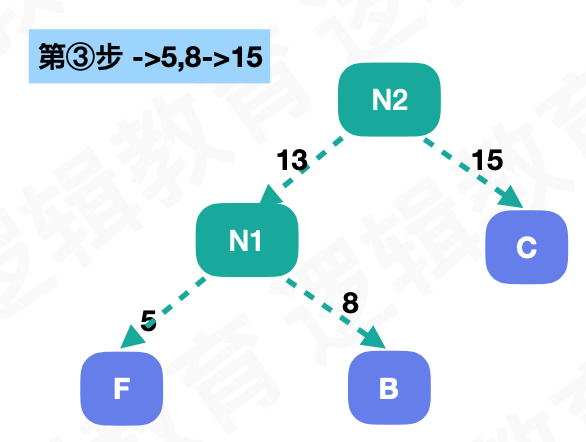
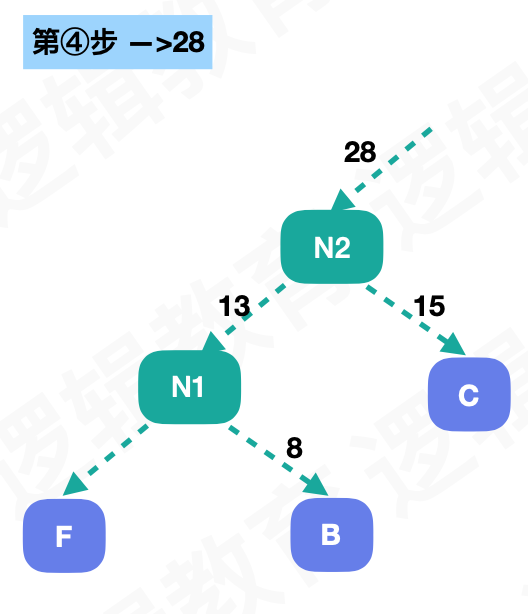
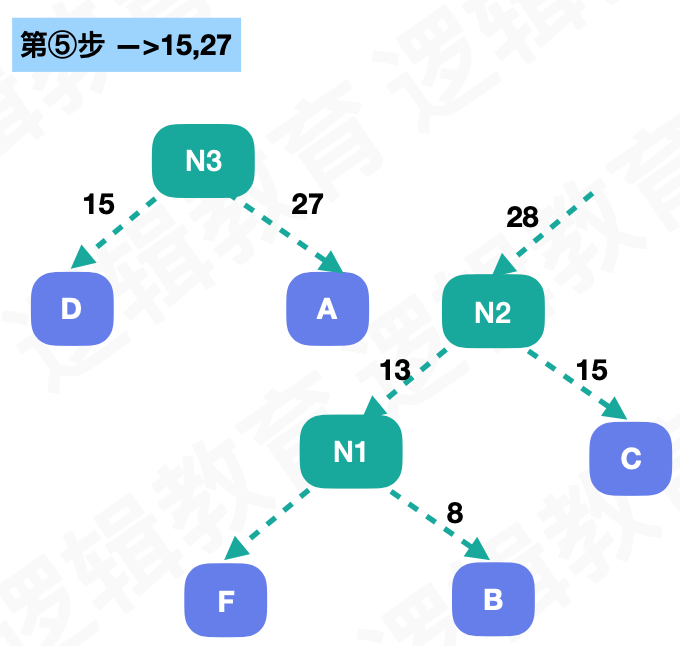
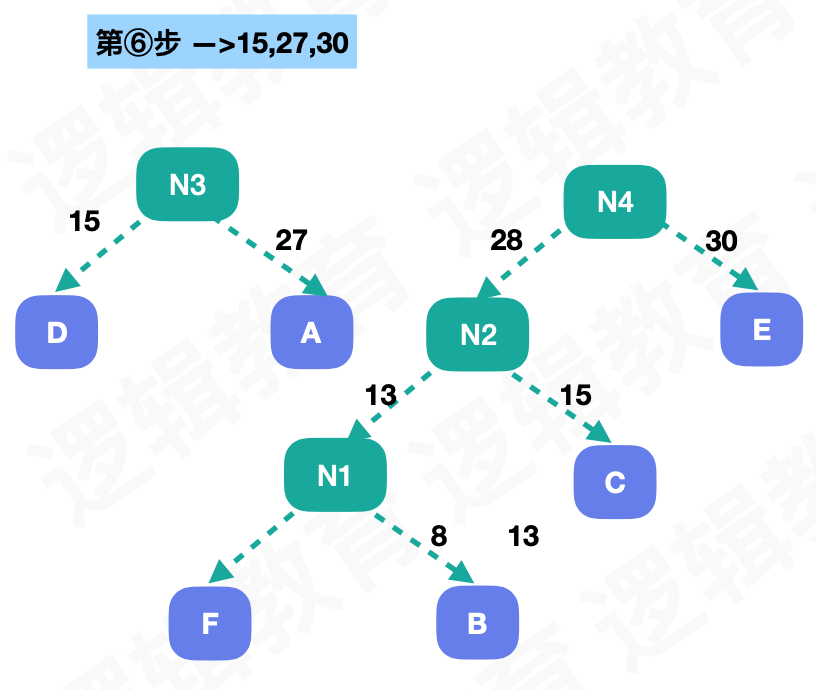
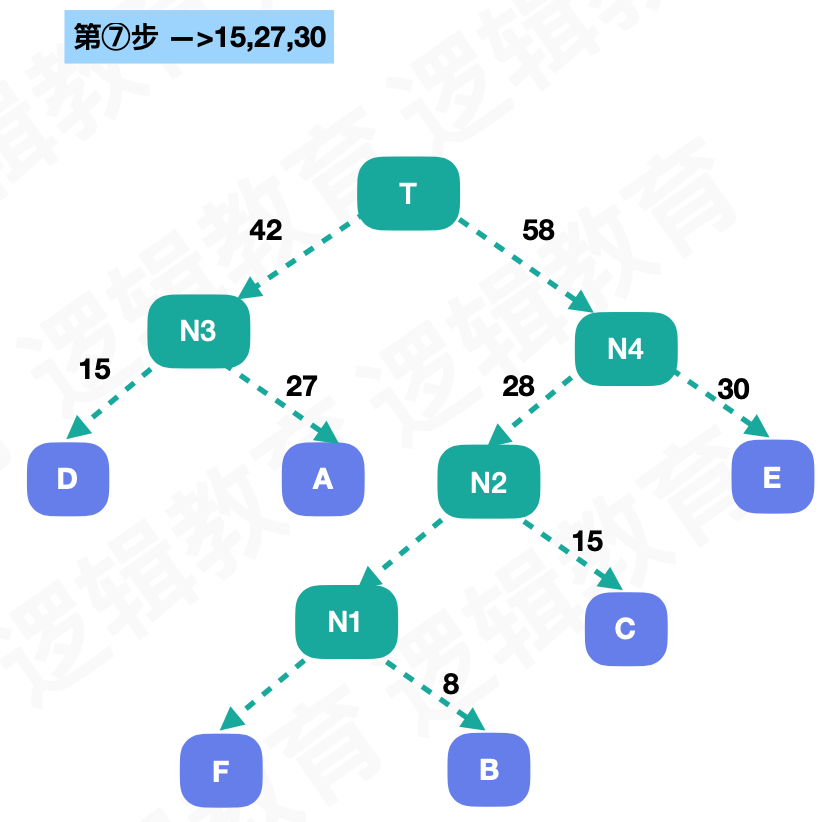
假如我们将左子树的路径叫做0,右子树的路径叫做1,我们通过路径来标示字符就能得到下面编码:
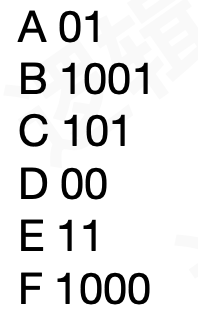

哈夫曼编码实现:
哈夫曼结点表现的形式


实现思路
哈夫曼树的实现思路路:
- 获取根据权值构建的哈夫曼树
- 循环遍历[0,n]个结点;
- 创建临时结点cd ,从根结点开始对⻬齐进⾏行行编码,左孩⼦子为0,右孩⼦子为1;
- 将编码后的结点存储haffCode[i]
- 设置HaffCode[i]的开始位置以及权值;
代码
const int MaxValue = 10000;//初始设定的权值最大值
const int MaxBit = 4;//初始设定的最大编码位数
const int MaxN = 10;//初始设定的最大结点个数
// 构建哈弗曼树的结点
typedef struct HaffNode {
int weight; // 权值
int flag; // 是否使用过
int parent; // 父节点索引
int leftChild; // 左儿子索引
int rightChild; // 右儿子索引
} HaffNode;
typedef struct Code//存放哈夫曼编码的数据元素结构,哈夫曼编码其实就是对应的数据(叶子节点)
{
int bit[MaxBit];//路径数组
int start; //编码的起始下标,相当于bit数组的下标
int weight;//字符的权值
}Code;
//1.
//根据权重值,构建哈夫曼树;
//{2,4,5,7}
//n = 4;
void Haffman(int weight[],int n,HaffNode *haffTree){
int j,m1,m2,x1,x2;
//1.哈夫曼树初始化
//n个叶子结点. 2n-1
for(int i = 0; i < 2*n-1;i++){
if(i<n)
haffTree[i].weight = weight[i];
else
haffTree[i].weight = 0;
haffTree[i].parent = 0;
haffTree[i].flag = 0;
haffTree[i].leftChild = -1;
haffTree[i].rightChild = -1;
}
//2.构造哈夫曼树haffTree的n-1个非叶结点
for (int i = 0; i< n - 1; i++){
m1 = m2 = MaxValue;
x1 = x2 = 0;
//2,4,5,7...j<n+i是因为i每遍历一次,haffTree数组里面就多设置了一个结点,也就是非叶子结点
for (j = 0; j< n + i; j++)//循环找出所有权重中,最小的二个值--morgan
{
if (haffTree[j].weight < m1 && haffTree[j].flag == 0)
{
m2 = m1;
x2 = x1;
m1 = haffTree[j].weight;
x1 = j;
} else if(haffTree[j].weight<m2 && haffTree[j].flag == 0)
{
m2 = haffTree[j].weight;
x2 = j;
}
}
//3.将找出的两棵权值最小的子树合并为一棵子树
haffTree[x1].parent = n + i;
haffTree[x2].parent = n + i;
//将2个结点的flag 标记为1,表示已经加入到哈夫曼树中
haffTree[x1].flag = 1;
haffTree[x2].flag = 1;
//修改n+i结点的权值
haffTree[n + i].weight = haffTree[x1].weight + haffTree[x2].weight;
//修改n+i的左右孩子的值
haffTree[n + i].leftChild = x1;
haffTree[n + i].rightChild = x2;
}
}
/*
9.2 哈夫曼编码
由n个结点的哈夫曼树haffTree构造哈夫曼编码haffCode
//{2,4,5,7}
*/
void HaffmanCode(HaffNode haffTree[], int n, Code haffCode[])
{
//1.创建一个结点cd,类似于temp,中间者
Code *cd = (Code * )malloc(sizeof(Code));
int child, parent;
//2.求n个叶结点的哈夫曼编码,haffTree的叶子节点都在最前面,非叶子节点在后面
for (int i = 0; i<n; i++)
{
//从0开始计数,
cd->start = 0;
//取得编码对应权值的字符
cd->weight = haffTree[i].weight;
//当叶子结点i 为孩子结点.
child = i;
//找到child 的双亲结点;
parent = haffTree[child].parent;
//由叶结点向上直到根结点,将该结点的路径找出来
while (parent != 0)
{
//得到一个编码
if (haffTree[parent].leftChild == child)
cd->bit[cd->start] = 0;//左孩子结点编码0
else
cd->bit[cd->start] = 1;//右孩子结点编码1
//编码下标自增
cd->start++;
//将双亲结点设置为子结点,往上遍历
child = parent;
//找到双亲结点
parent = haffTree[child].parent;
}
int temp = 0;
//把cd中的数据赋值到haffCode[i]中.
for (int j = cd->start - 1; j >= 0; j--){
temp = cd->start-j-1;
haffCode[i].bit[temp] = cd->bit[j];
}
//保存好haffCode 的起始位以及权值;
haffCode[i].start = cd->start;
//保存编码对应的权值
haffCode[i].weight = cd->weight;
}
}
int main(int argc, const char * argv[]) {
// insert code here...
printf("Hello, 哈夫曼编码!\n");
int i, j, n = 4, m = 0;
//权值
int weight[] = {2,4,5,7};
//初始化哈夫曼树, 哈夫曼编码
HaffNode *myHaffTree = malloc(sizeof(HaffNode)*2*n-1);
Code *myHaffCode = malloc(sizeof(Code)*n);
//当前n > MaxN,表示超界. 无法处理.
if (n>MaxN)
{
printf("定义的n越界,修改MaxN!");
exit(0);
}
//1. 构建哈夫曼树
Haffman(weight, n, myHaffTree);
//2.根据哈夫曼树得到哈夫曼编码
HaffmanCode(myHaffTree, n, myHaffCode);
//3.
for (i = 0; i<n; i++)
{
printf("Weight = %d\n",myHaffCode[i].weight);
for (j = 0; j<myHaffCode[i].start; j++)
printf("%d",myHaffCode[i].bit[j]);
m = m + myHaffCode[i].weight*myHaffCode[i].start;
printf("\n");
}
printf("Huffman's WPS is:%d\n",m);
return 0;
}