算法 - 递归

本文为小码哥推出的恋上数据结构与算法笔记，如有兴趣，请报班学习

斐波那契数列

public class Fib {
	public static void main(String[] args) {
		Fib fib = new Fib();
		System.out.println(fib.fib5(5));
		
	}
	
//	 第一种
	int fib0(int n) {
		if (n <= 2) return 1;
		return fib0(n - 2) + fib0(n  - 1) ;
	}
	
//	优化一：利用数组存放计算过的结果，避免重复计算
	int fib1(int n) {
		if (n <= 2) return 1;
		int[] array = new int[n+1];
		array[2] = array[1] = 1;
		return fib1(n, array);
	}
	
	int fib1(int n, int[] array) {
		if (array[n] == 0) {
			array[n] = fib1(n - 1, array) + fib1(n-2, array);
		}
		return array[n];
	}
//	优化二：去递归调用
	int fib2(int n) {
		if (n <= 2) return 1;
		int[] array = new int[n+1];
		array[2] = array[1] = 1;
		for (int i = 3; i <= n; i++) {
			array[i] = array[i-1] + array[i-2];
		}
		return array[n];
	}
//	优化三：滚动数组
	int fib3(int n) {
		if (n <= 2) return 1;
		int[] array = new int[2];
		array[0] = array[1] = 1;
		for (int i = 3; i <= n; i++) {
			array[i%2] = array[(i-1) % 2] + array[(i-2) % 2];
		}
		return array[n % 2];
	}
//	优化四：位运算取代模运算  (对于2的模运算，相当于取2进制的最后一位，相当于位运算的 & 1)
	int fib4(int n) {
		if (n <= 2) return 1;
		int[] array = new int[2];
		array[0] = array[1] = 1;
		for (int i = 3; i <= n; i++) {
			array[i & 1] = array[(i-1) & 1] + array[(i-2) & 1];
		}
		return array[n & 1];
	}
//	优化五：利用两个数字来替换数组
	int fib5(int n) {
		if (n <= 2) return 1;
		int first = 1;
		int second = 1;
		for (int i = 3; i <= n; i++) {
			second = first + second;
			first = second - first;
		}
		return second;
	}
}

爬楼梯

一次可以上一步或者两步台阶，上到第N阶需要多少步？ 参考 ：算法——爬楼梯问题

下面的图是我偷过来的。。建议看看原文

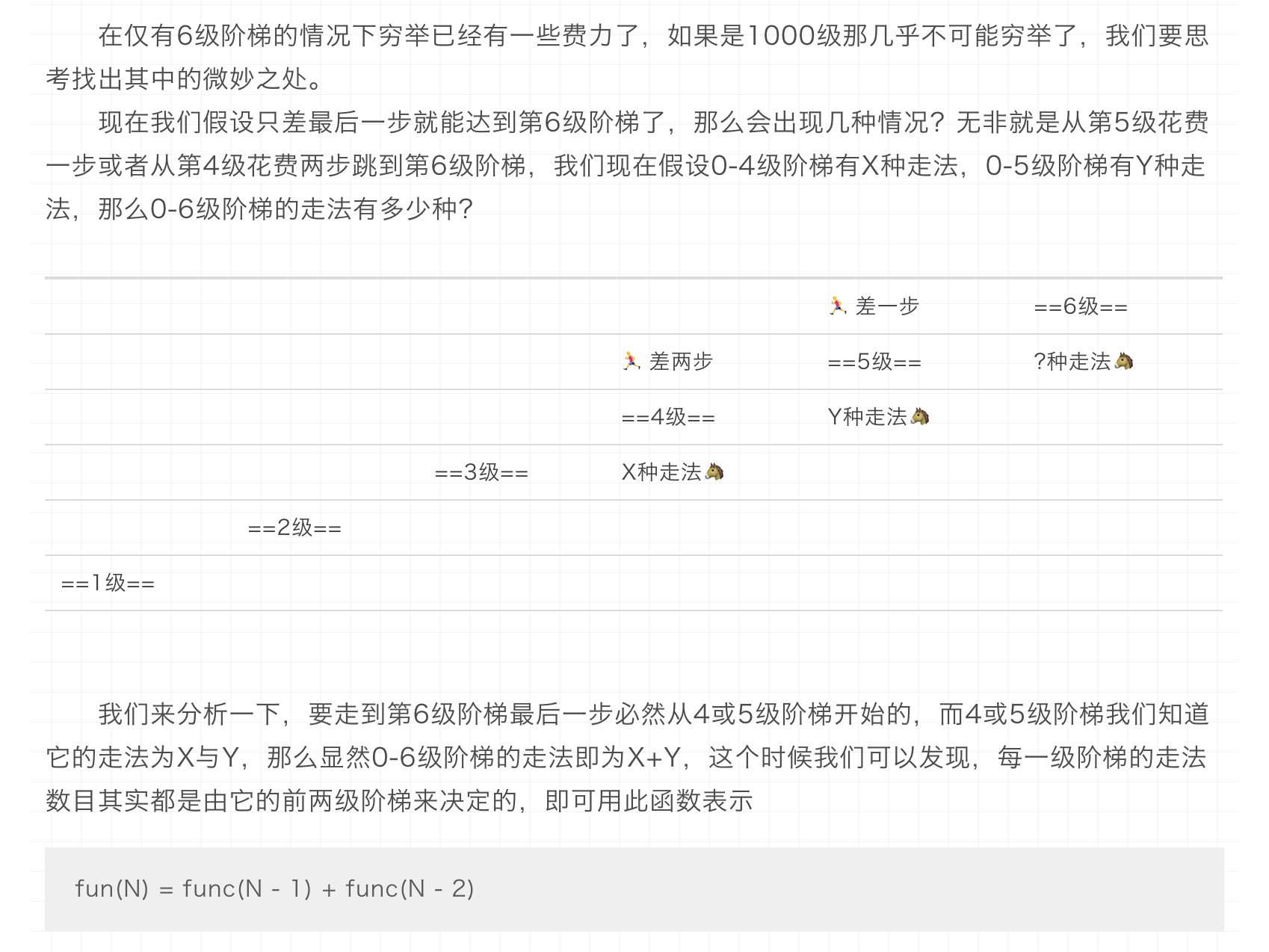
可以看出是和斐波那契数列相同的迭代

public class ClimbStairs {
	int climbStairs(int n) {
		if (n <= 2) return n;
		return climbStairs(n - 1) + climbStairs(n - 2);
	}
	
}

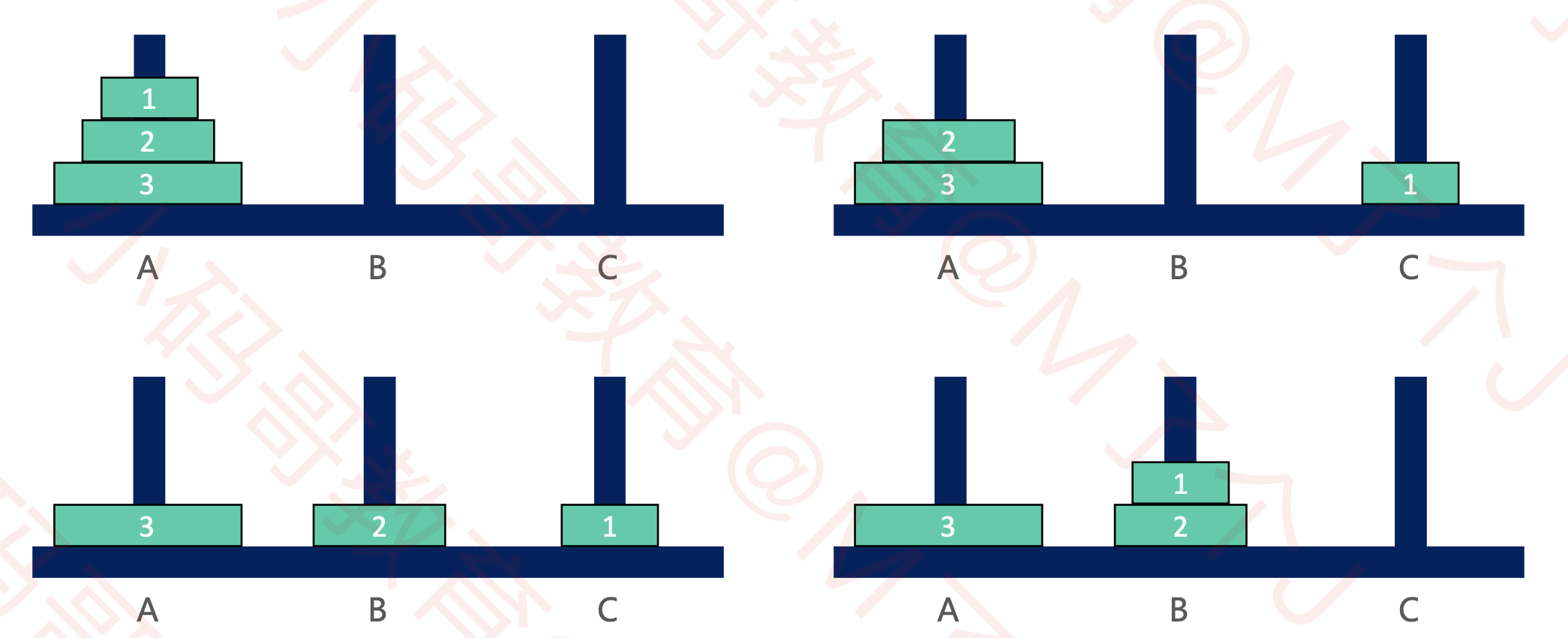
汉诺塔

思路： 观察可以得出规律是从A柱搬运p(n-1)到B柱，将p(n)从A柱搬运到C柱，将p(n-1)从B柱搬运到C柱

public class Hanoi {
	public static void main(String[] args) {
		new Hanoi().hanoi(3, "A", "B", "C");
	}
	
	/**
	 * 将 n 个碟子从 p1 挪动到 p3
	 * @param p2 中间的柱子
	 */
	void hanoi(int n, String p1, String p2, String p3) {
		if (n <= 1) {
			move(n, p1, p3);
			return;
		}
		hanoi(n-1, p1, p3, p2);
		move(n, p1, p3);
		hanoi(n-1, p2, p1, p3);
	}
	
	/**
	 * 将 no 号盘子从 from 移动到 to
	 * @param no
	 * @param from
	 * @param to
	 */
	void move(int no, String from, String to) {
		System.out.println("将" + no + "号盘子从" + from + "移动到" + to);
	}
}