问题描述
Given a binary tree, find the length of the longest path where each node in the path has the same value. This path may or may not pass through the root.
The length of path between two nodes is represented by the number of edges between them.
Example 1:
Input:
5
/ \
4 5
/ \ \
1 1 5
Output: 2
Example 2:
Input:
1
/ \
4 5
/ \ \
4 4 5
Output: 2
Note:
The given binary tree has not more than 10000 nodes. The height of the tree is not more than 1000.
最开始读题的时候我理解错了题意,再加上给的例子也不是很全面化。我最开是理解的是所有值相同,且都有连接的节点之间的距离。但是其实题目是要求的在值相等且互相连接的节点中找出一条最长路径(这里路径的长度就是这些节点之间边的数量和)。所以最初我一直怀疑官方给出的答案有误......所以最重要的是认真审题!认真审题!认真审题!
理解了题意后,我们会意识到这是一个关于树结构的算法题目。而往往在有关于树结构的算法,一般会涉及到递归的操作,以及树结构的各种特性。
思路:
仔细观察了题目中给的例子以及理解了题意后我们其实可以察觉到一些规律。在找寻这些路径的时候有一个特点,这些路径总是由经过某一个节点然后延伸到子节点的,假设我们现在要确定节点i的与子节点有没有一条这样的路径,首先我们需要判断节点i的值与两个一级子节点是否相等,只有相等的条件下路径才会从节点i延伸出去。同理,我们要确定i的子节点与子节点的子节点有没有存在这样的路径,也是先判断值。最后我们会发现,如果从节点i确有一条路径通过子节点延伸出去,那么这条路径的长度应该是等于,两个子节点与子节点之后的子节点的路径长度分别加一(因为子节点和i也有路径),之后求和。
经过以上的分析,求经过当前节点最长等值路径的问题就转换成了分别求经过当前节点两个子节点的最长等值路径之和了。然后继续拆分下去,就是一个递归问题。
既然是递归问题,那么递归返回的条件判断非常重要,当然在这个问题中递归函数返回的条件就是当前节点为null。
代码示例:
class Solution {
//用于递归调用时的全局变量记录当前已经找到的最长路径的长度
int pathLength;
public int longestUnivaluePath(TreeNode root) {
pathLength = 0;
length(root);
return pathLength;
}
//递归主题函数
public int length(TreeNode node) {
//返回条件
if (node == null) return 0;
//先递归左边的子节点
int subLeftLength = length(node.left);
int subRightLrngth = length(node.right);
//声明两个记录变量,这两个变量是用来后面判断路径是否存在
int leftLength = 0, rightLength = 0;
//如果当前节点的左子节点不为空,且值与当前节点的值也相等,则当前节点与
//左子节点和左子节点之后的子节点是存在等值路径的,再计算路径长度
if (node.left != null && node.left.val == node.val) {
leftLength = subLeftLength + 1;
}
//同上
if (node.right != null && node.right.val == node.val) {
rightLength = subRightLrngth + 1;
}
//让当前寻找到的等值路径长度和记录的最长等值路径长度比较,取大的一个
pathLength = Math.max(pathLength, leftLength + rightLength);
//这里这个返回值特别重要 ,也是特别不好理解的一个地方
return Math.max(leftLength, rightLength);
}
}
上面代码中对递归函数返回值的理解特别重要。我们知道如果我们要递归调用,第一个要确定的是返回的临界条件,另外一个就是函数的返回值到底是什么。
这里的返回值是左右字节点最长路径的较大值,为什么我们会这样选则呢?
其实可以这样理解,我们如果要计算以当前节点为根节点的等值路径的长度时,我们当然是让以左右子节点为根节点的最长等值路径相加。但是这里我们是需要返回给上一层调用节点的,相当于当前节点的父节点来问当前节点:“小老弟,经过你的等值最长路径的值是多少啊?” 当前节点跟大哥肯定不能说假话,而且一条路径到了当前节点肯定是不能分叉的,要选择其中一条,所以当前节点就选择了最长的一条路径返回给了父节点。
我们现在来分析下算法的时间和空间复杂度
由于我们用了递归,而且树结构的所有节点都会被遍历到,其实那些在树结构中为null的节点也会遍历到。所以我们的时间复杂度就是O(n).
那么空间复杂度呢?
我们递归调用函数肯定要用到栈,那么栈的最大深度是多少,就是空间复杂度了。
那么栈的最大深度是多少呢?
我们以例子1来画图演示.
我们从根节点开始调用length()函数,然后先递归调用左子节点,程序的栈区如下图。

当所有的左子节点都完成后,执行函数栈的最顶端的函数,即出栈:
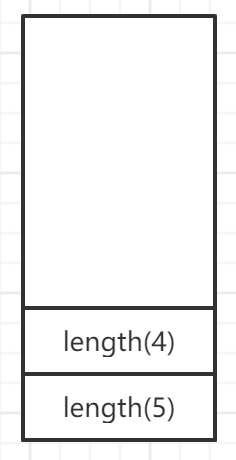
在执行出栈length(1)后,又会出栈length(4),但是在执行length(4)的时候,4的右子节点又会进栈:

所以最后我们会发现,栈的最深size就是整个树结构的最大深度。
所以空间复杂度是:O(Height of Tree).
这道题到此结束。但是引发了我的一些思考,我其实觉得这个题不止是easy的难度,哈哈。然后这种解法其实也是对树结构的通常算法思路,所以对树结构,递归操作,程序函数栈的调用以及深度搜索比较熟悉的同学思考这道题可能会比较有优势。