问题描述
Give an array on integers A, find the sum of min(B), where B ranges over every (contiguous) subarray of A .
Since the answer may be large, return the answer modulo 10^9 + 7 .
Example 1:
Input: [3, 1, 2, 4]
Output: 17
Explanation: Subarrays are [3], [1], [2], [4], [3,1], [1,2], [2,4], [3,1,2], [1,2,4], [3,1,2,4].
Minimums are 3, 1, 2, 4, 1, 1, 2, 1, 1, 1. Sum is 17.
Note:
1. <font color=gray>1 <= A.length <= 30000</font>
2. <font color=gray>1 <= A[i] <= 30000</font>
第一次读题的时候没有读懂什么意思,感觉总体题的意思比较绕。还是看了例子才明白什么意思的.......
所以,要认真审题!认真身体!认真审题!
总体来说题目的意思是:给定一个整形数组,求所有连续子数组的最小值的和。
需要注意的是,需要考虑到给定的整形数组有条件限制。长度1~30000, 数组里值1~3000。
读懂题后的第一反应是肯定有两种以上的解法。
第一种解法: 暴力解题
思路:先找出所有所有的子数组,再确定每个子数组的最小值,最后求和。
缺点:这种解法的缺点太明显了。时间经计算是大于 O(n^2), 空间复杂度是O(n^3)。所以不可取
第二种解法:利用单调栈(monotonic stack)
思路:其实我们在用暴力解这题的时候会发现有很多连续子数组的最小值都是重复的,那么我们可不可以利用这个现象去寻找一种办法能够存储下最小值呢?这里展开讲一下,有点类似于数学函数中局部最小,于是我想到在对一个数学函数于指定的变量区间内求局部最小值的方法和特点。局部最小值是函数变量在一个区间内的函数最小值,注意这个变量的区间。区间的定义是什么? X1~X2之间的所有变量对不对?那么我们可以将变量对应到我们的数组下标。
再深入下:假设我们现在有一个局部最小值,会发现这局部最小值也是这个区间的所有子区间的局部最小函数值(这里的子区间一定要包括局部最小值对应的变量!!)。那么类似的,假设现在**A[i]是某一个连续子数组的最小值,那么可以由此得出A[i]也是所以数组下标在这个连续子数组内的其他子数组的最小值。现在我们就可以转变成A[i]最多可以是多少个连续子数组的最小值,到了这一步就比较明了了,下一步就是确定A[i]**两边比它小的值的边界下标。
假设离A[i]相距leftDistance的是比A[i]小的元素,离A[i]相距rightDistance的是另外一个比**A[i]小的元素。那么A[i]**是下标在(i - leftDistance)~(i + rightDistance)所有连续子数组的最小值(当然这个连续子数组要包括i)。
好了,那么怎么求离A[i]元素前后最近的比它小的元素的距离呢?换一句话说,在数组中我们要求指定元素的下一个和前一个比它小的元素与它的距离。单调栈!单调栈!单调栈!
单调栈是什么?
单调栈是一种特殊的栈结构,在栈中的所有元素是有序且单调性一致的。意思就是栈中元素要么升序,要么降序。假如是单点递增栈:每当像栈中添加元素时,需要比对栈顶的元素,如果小于栈顶的元素就需要先出栈一直到栈顶元素小于等于插入元素的时候再将新元素入栈。
那么我们如何用单调栈解题呢?
设想一下,我们现在有数组[1, 5, 5, 2, 4, 3, 2, 1, 5], 现在我们要利用单调递增栈来求下标i=3元素离比它小的下一个元素的距离。
我们先让i=3的元素进栈:
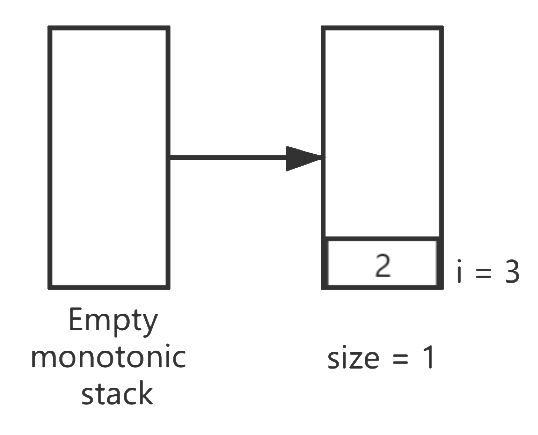
然后比较新添加的元素与栈顶元素的大小关系:
if(newElement > peekElement) {
stack.push();
}
else {
stack.pop();
}
下一个元素是4,4 > 2所以继续进栈:
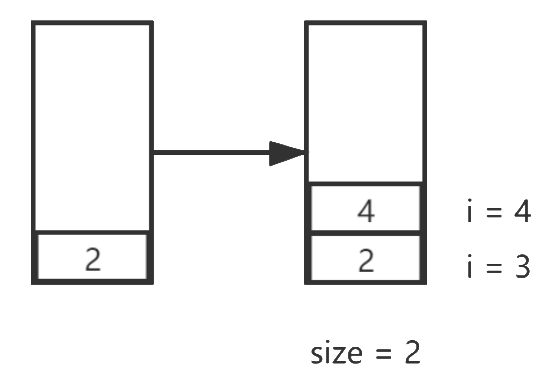
下一个元素是3, 3 < 4,所以应该出栈:
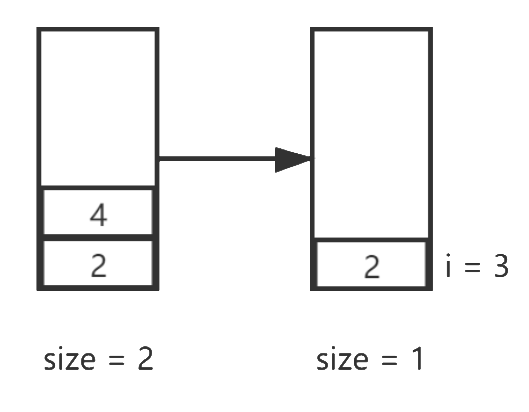
注意这次元素4的出栈其实可以确定元素4离右边最近一个比它小的元素的距离是1,所以我们可以用一个数组来记录这些距离值:
//存储每一个元素离前一个比它小的元素的距离
int[] prevSmallerOrEqual = new int[A.length];
//存储每一个元素离后一个比它小的元素的距离
int[] nextSmaller = new int[A.length];
当4出栈的时候我们可以给距离数组赋值,再出栈**(记住我们在栈中存储的一直是元素的下标,图中将元素值存到栈中是因为便于理解!!!所以此处stack.peek() == 4)**
nextSmaller[stack.peek()] = i - ascendingStack.peek() - 1;
ascendingStack.pop();
元素4出栈后,元素3就可以进栈了。单调栈就体现在这里!!!因为每次添加新的元素时,都需要将栈顶所有大于新元素的对象清除掉,然后再把新的元素进栈:
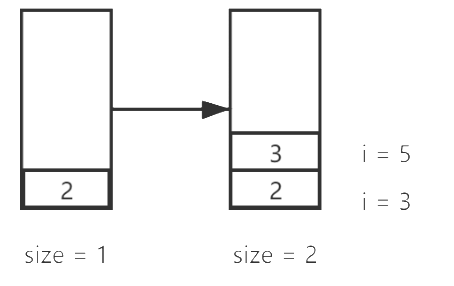
下一次需要进栈的元素是2,然后重复上面的操作,先把栈顶元素与新元素比较,需要出栈:
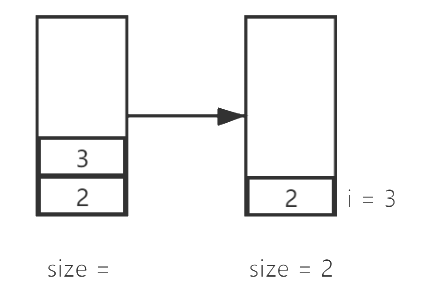
然后新元素可以进栈了:
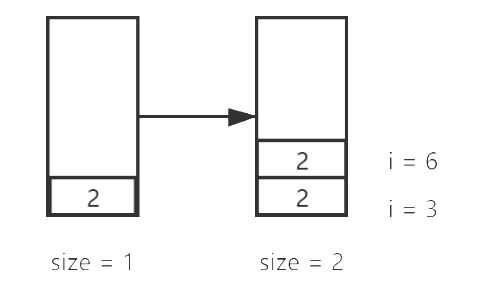
注意一下,我们在往后面找比当前元素小的元素的时候,遇到跟自己值相等的元素是可以添加进栈的,但是往前找比自己小的时候需要改变一下条件,遇到与自己相等的元素是不可以直接入栈的。这样是为了避免如果数组中有重复的元素,会造成重复计数。
比如例子中的数组:[1, 2, 5, 2, 4, 3, 2, 1, 5], 当前我们需要寻找i=3元素离前一个小于它的值和后一个小于它的值的距离。如果我们的条件都是>的话,试一下结果。
结果应该是区间:[2, 5, 2, 4, 2]
但是当按照上述规则寻找i=2元素的区间应为:[2, 5, 2, 4, 2]
发现区间重复了,所以我们需要修改向前寻找后向后寻找的临界条件。
好了注意到了上面的一个小trick,我们继续。下一步需要入栈的元素是1,1小于栈顶的2,所以2需要先出栈:
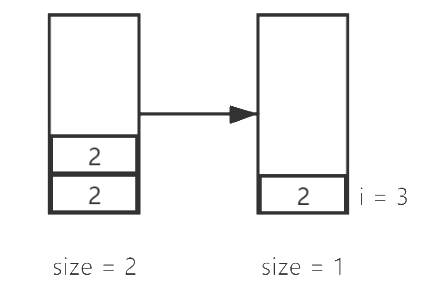
到了这里我们基本就结束了,此时我们已经遍历到了i=7,值为1的元素,而栈中就是我们的基准元素。所以i=3的元素离下一个比它小的元素的距离就是7 - 3,也就说明,i=3有7 - 3 - 1个元素比它大,然后接着就是比它小的元素。
在成功找到后,我们还是需要维护单调栈的,为下一个元素做准备。
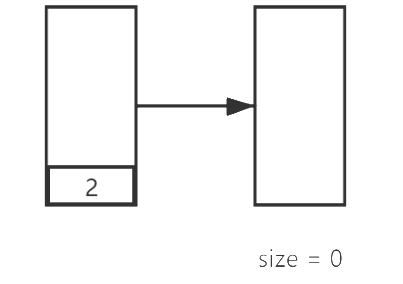
然后新元素1进栈:
好了,至此结束了寻找i=3元素离下一个小于它的元素的距离。之后所有的元素可以依此类推。
代码示例:
//向右找下一个比A[i]小的元素的下标j,将nextSmaller[i] = j - i - 1;
for (int i = 0; i < nextSmaller.length; i++) {
while(!ascendingStack.empty() && A[ascendingStack.peek()] > A[i]) {
nextSmaller[ascendingStack.peek()] = i - ascendingStack.peek() - 1;
ascendingStack.pop();
}
ascendingStack.push(i);
}
//清空ascendingStack
while(!ascendingStack.empty()) {
nextSmaller[ascendingStack.peek()] = A.length - ascendingStack.peek() - 1;
ascendingStack.pop();
}
一定会注意到上面代码中第二个while循环在清空栈,为什么呢?
这是因为存在for循环结束后,栈中依然存在元素,而此时栈中元素都是升序排列的,说明后面都没有比它们小的元素了。所以可以便出栈,边计算出栈元素的右边界值。
根据上面寻找右边界的逻辑,可以向前寻找左边界。只需要注意寻找的时候,出入单调栈的临界条件需要改变下。
代码示例:
//向左找上一个比A[i]小的元素的下标j,将prevSmallerOrEqual[i] = i - j - 1;
for (int i = prevSmallerOrEqual.length - 1; i >= 0; i--) {
while(!ascendingStack.empty() && A[ascendingStack.peek()] >= A[i]) {
prevSmallerOrEqual[ascendingStack.peek()] = ascendingStack.peek()-i-1;
ascendingStack.pop();
}
ascendingStack.push(i);
}
//清空ascendingStack
while(!ascendingStack.empty()) {
prevSmallerOrEqual[ascendingStack.peek()] = ascendingStack.peek();
ascendingStack.pop();
}
上面所示的向前寻找边界值的代码注意是从后往前循环的。
经过上面的代码,我们寻找到了每个元素作为最小值的最大边界值,之后我们就可以计算了。
边界的大小和连续子数组之间是有规律的。比如上面的例子中以i=3的元素为最小值的最大边界是i=1~i=7,即数组区间为[5, 5, 2, 4, 3, 2],左边界距=2,右边界距=3。包含i=3元素的所有连续子数组(在这个数组区间)的个数满足
(左边界距 + 1) * (右边界距 + 1) = 12,说明2这个元素在这个区间的子数组出现的次数是12次,所以2*12 = 24.之后我们就可以累计求和。
求和代码:
BigDecimal notModResultBigDecimal = new BigDecimal(0);
//计算所有连续子数组的最小值之和
for (int i = 0; i < A.length; i++) {
int count = (prevSmallerOrEqual[i] + 1) * (nextSmaller[i] + 1);
notModResultBigDecimal =
notModResultBigDecimal.add(new BigDecimal(A[i] * count));
}
好了到了此处,我们用单调栈和该题的规律解决了这个medium难度的问题。再接再厉
我们来看一下算法的时间和空间复杂度。
时间复杂度:
通过观察,每个数组中的元素都会入栈和出栈一次所以时间复杂度是O(n)
空间复杂度:
通过计算是O(n)